Учебная работа № 2080. Синтез оптимальных уравнений
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Механикоматематический факультет
Кафедра теоретической механики и робототехники
Курсовая работа
Тема: Синтез оптимальных уравнений
Студента 3го курса 13 группы
Павловского Сергея Александровича
Научный руководитель
Лютов Алексей Иванович
Минск 2001г.
Г л а в а I. …………………………………………………………………………………… 2
§ 1. Задача об оптимальном быстродействии……………………………………………. 2
1.Понятие об оптимальном быстродействии………………………………………….. 2
2.Задача управления……………………………………………………………………………. 3
3.Уравнения движения объекта…………………………………………………………….. 5
4.Допустимые управления……………………………………………………………………. 6
§ 2. Об основных направлениях в теории оптимальных процессов……………… 7
5.Метод динамического программирования………………………………………….. 7
6.Принцип максимума…………………………………………………………………………. 9
§ 3. Пример. Задача синтеза……………………………………………………………………. 12
7.Пример применения принципа максимума……………………………………….. 12
8.Проблема синтеза оптимальных управлений…………………………………….. 14
Г л а в а II. Линейные оптимальные быстродействия ………………………………. 15
§ 4 Линейная задача оптимального управления……………………………………….. 15
9.Формулировка задачи…………………………………………………………………….. 15
10.Принцип максимума……………………………………………………………………… 16
11.Принцип максимума — необходимое и достаточное условие
оптимальности………………………………………………………………………………….. 17
12.Основные теоремы о линейных оптимальных быстродействиях……….. 18
§ 5. Решение задачи синтеза для линейных задач второго порядка……………. 18
13.Упрощение уравнений линейного управляемого объекта…………………. 18
Г л а в а III. Синтез оптимальных управлений для уравнения второго
порядка ……………………………………………………………………………………………. 20
§ 6. Решение задачи синтеза в случае комплексных собственных значений…… 20
14.Задача синтеза для малых колебаний маятника……………………………….. 20
Список используемой литературы…………………………………………………………….. 23
Г л а в а I
ВВЕДЕНИЕ
Управляемые объекты прочно вошли в нашу повседневную жизнь и стали обиходными, обыденными явлениями. Мы видим их буквально на каждом шагу: автомобиль, самолёт, всевозможные электроприборы, снабжённые регуляторами (например, электрохолодильник), и т. п. Общим во всех этих случаях является то, что мы можем «управлять» объектом, можем в той или иной степени влиять на его поведение.
Обычно переход управляемого объекта из одного состояния в другое может быть осуществлён многими различными способами. Поэтому возникает вопрос о выборе такого пути, который с некоторой (но вполне определённой) точки зрения окажется наиболее выгодным. Это и есть (несколько расплывчато сформулированная) задача об оптимальном управлении.
§ 1. Задача об оптимальном быстродействии
1. 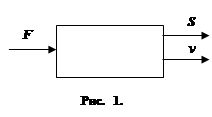 Понятие об управляемых объектах. Рассмотрим прямолинейное движение автомобиля. В каждый момент времени состояние автомобиля можно характеризовать двумя числами: пройденным расстоянием s и скоростью движения v. Эти две величины меняются с течением времени, но не самопроизвольно, а сообразно воле водителя, который может по своему желанию управлять работой двигателя, увеличивая или уменьшая развиваемую этим двигателем силу F. Таким образом, мы имеем три связанных между собой параметра: s ,v ,F ,показанных на схеме (рис. 1). Величины s ,v ,характеризующие состояние автомобиля, называют его фазовыми координатами ,а величину
Понятие об управляемых объектах. Рассмотрим прямолинейное движение автомобиля. В каждый момент времени состояние автомобиля можно характеризовать двумя числами: пройденным расстоянием s и скоростью движения v. Эти две величины меняются с течением времени, но не самопроизвольно, а сообразно воле водителя, который может по своему желанию управлять работой двигателя, увеличивая или уменьшая развиваемую этим двигателем силу F. Таким образом, мы имеем три связанных между собой параметра: s ,v ,F ,показанных на схеме (рис. 1). Величины s ,v ,характеризующие состояние автомобиля, называют его фазовыми координатами ,а величину

 (6 оценок, среднее: 4,67 из 5)
(6 оценок, среднее: 4,67 из 5)