Учебная работа № 2004. Различные подходы к определению проективной плоскости
Содержание
Исторический обзор аксиоматического построения проективной геометрии
Глава 1. Определение проективной плоскости на базе трехмерного
векторного пространства.
1.1. Понятие проективной плоскости.
1.2. Свойства проективной плоскости.
1.3. Модели проективной плоскости.
1.4. Теорема Дезарга.
1.5. Теорема Паппа.
Глава 2. Аналитическое построение проективной плоскости.
2.1. Понятие проективной плоскости.
2.2. Свойства проективной плоскости.
2.3. Теорема Дезарга.
Глава 3. Аксиоматическое построение проективной плоскости.
3.1. Аксиоматика аффинной плоскости.
3.2. Аксиоматика проективной плоскости.
3.3. Модели проективной плоскости.
3.4. Теорема Дезарга.
3.5. Принцип двойственности.
3.6. Гармоническая четверка точек.
3.7. Перспективные и проективные отображения.
3.8. Аксиома Паппа и основная теорема о проективных преобразованиях прямой.
Глава 4. Применение основных теорем к решению задач на евклидовой плоскости.
4.1. Использование теоремы Дезарга на евклидовой плоскости.
4.2. Использование предложения Паппа на евклидовой плоскости.
Приложения
Список литературы
Понятие проективной плоскости можно ввести многими способами. Проективную плоскость можно построить на базе трехмерного векторного пространства, аналитически и аксиоматически.
В данной работе, в ее первой главе, проективная плоскость Р2 строится на базе трехмерного векторного пространства, рассматриваются свойства проективной плоскости и ее модели. В конце главы доказываются теоремы: Дезарга и Паппа.
Во второй главе проективная плоскость рассматривается как множество проективных точек, каждая из которых представляет собой класс пропорциональных троек действительных чисел, не содержащей нулевой тройки. При данном подходе к построению проективной плоскости рассматриваются свойства, доказывается теорема Дезарга.
В третьей главе уделяется внимание построению проективной плоскости аксиоматически. Прежде чем определить проективную плоскость, вводится аксиоматика аффинной плоскости. После определения проективной плоскости рассматриваются 4 ее модели. Особое внимание уделяется теореме Дезарга. На основе изложенного в третьей главе материала делается вывод о двойственности на проективной плоскости. В этой главе также определяются понятия: гармоническая четверка точек, перспективные и проективные отображения. Завершает главу аксиома Паппа и основная теорема о проективных преобразованиях прямой.
Глава четвертая изучает использование теорем Дезарга и Паппа на евклидовой плоскости. После чего приводятся решения задач, при решении которых использовались доказанные выше теоремы.
Вся история геометрии дает поучительный пример того, как эта наука материальные корни которой берут свое начало из жизненных потребностей человеческого общества (землемерие, постройка жилищ, живопись), достигла высокого теоретического уровня, выработала свои специфические и вместе с тем весьма общие методы, которые в свою очередь сделали возможным новые плодотворные применения геометрии к практическим вопросам.
Исторический обзор аксиоматического построения проективной геометрии.
Имеются различные аксиоматические способы построения проективного пространства. Наиболее распространенным является видоизменение системы аксиом, предложенной в 1899 году Гильбертом для обоснования элементарной геометрии.
Проективное пространство рассматривается как совокупность элементов трех родов: точек, прямых и плоскостей, между которыми установлено основное для проективной геометрии отношение инцидентности, характеризующееся надлежащими аксиомами. Они отличаются от соответствующих групп аксиом элементарной геометрии, тем, что требуют, чтобы каждые две прямые, лежащие в одной плоскости, имели общую точку и на каждой прямой имелось, по крайней мере, три различные точки. В конкретных случаях для получения более “богатой” проективной геометрии эта совокупность аксиом дополняется аксиомами порядка и непрерывности (для действительного проективного пространства), аксиома Паппа (для проективной геометрии над коммутативными телами), Фано постулатом (для проективной геометрии над телами, характеристика которого порядка ¹2) и т.д.
Замечательным положением проективной геометрии является принцип двойственности. Говорят, что точка и прямая (точка и плоскость, прямая и плоскость) инцидентны, если точка лежит на прямой (или прямая проходит через точку и т.д.). Тогда если верно некоторое предположение А о точках, прямых и плоскостях проективного пространства, сформулированные только в терминах инцидентности между ними, то будет верно и двойственное предложение В, которое получается из А заменой слова “точка” на слово “плоскость”, слово “плоскость” на слово “точка” и с сохранением слова прямая.
Важную роль в проективной геометрии играет Дезарга предложение, выполнение которого необходимо и достаточно для введения проективными средствами системы проективных координат, составленных их элементов некоторого тела К, естественным образом связанного с точкой проективной прямой.
Основы проективной геометрии заложены в 17в Ж. Дезаргом и Б. Паскалем. Большое значение для последующего развития проективной геометрии имели работы П. Монтена (2я полов. 18в – нач. 19в).
Как самостоятельная дисциплина проективная геометрия была изложена Понселе (нач. 19в). Заслуга Ж. Понселе заключается в выделении проективных свойств фигур в отдельный класс, и установлении соответствий между метрическими и проективными свойствами этих фигур.
К этому же периоду относятся работы Ж. Брионшона. Дальнейшее развитие проективная геометрия получила в трудах Я. Штейнера и М. Шаля. Большую роль в развитии проективной геометрии сыграли работы К. Штаудта, в которых были намечены также контуры аксиоматического построения проективной геометрии.
Все эти геометрии, стремились доказать теоремы проективной геометрии синтетическим методом, положив в основу изложенные проективные свойства фигур.
Аналитическое направление в проективной геометрии было намечено работами А. Мебиуса. Влияние на развитие проективной геометрии оказали работы Н.И. Лобачевского по созданию неевклидовой геометрии, позволившие в дальнейшем А. Кэли и Ф. Клейну рассмотреть различные геометрии, систематизировать с точки зрения проективной геометрии.
Развитие аналитических методов обычной проективной геометрии и построение на этой базе комплексной проективной геометрии поставили задачу о зависимости тех или иных проективных свойств от того тела, над которым построена геометрия. В решении этого вопроса больших успехов добились А.Н. Колмогоров и Л.С. Понтрягин.
Глава 1. Определение проективной плоскости на базе трехмерного векторного пространства.
1.1. Понятие проективной плоскости.
Рассмотрим определение проективной плоскости Р2. Понятие проективной плоскости строится на базе трехмерного векторного пространства V3.
Определение: Не пустое множество Р2 называется проективным плоскостью, если существует отображение j множества ненулевых векторов V3 в Р2 удовлетворяющее двум условиям:
1) Отображение j сюрьективно.
2) Образы 2х векторов совпадают, эти векторы линейно зависимы.
j(х)=j(у)Û х,у – линейно зависимы.
1.2. Свойства проективной плоскости.
Рассмотрим свойства проективной плоскости Р2.
1) Через » две () проективной плоскости проходит единственная прямая.
Доказательство: Рассмотрим проективную плоскость Р2 построенную на базе V3.
Пусть точка А порождена векторомаÎV3 (т.е. j(а)=А).
() В порождена b ÎV3(т.е. j(b )=В);
a//b т.к. порождают различные точки. Тогда на вектора a , b можно натянуть двумерное векторное пространство L (a ,b ), которое на проективной плоскости порождает прямую l . Очевидно прямая l проходит через () А и В.
V1(а )=A V1ÌV2 Þ AÎl
V1(b )=B V1’ÌV2 ÞB Îl
Единственность: Действительно, пусть l ‘ произвольная прямая проходящая через () А и В, а L ‘ двумерное подпространство, которое порождает прямую l ‘ так как АÎl ‘ и ВÎl ‘, то аÎL ‘ и b ÎL ‘ ÞL ‘ подпространство натянутое на векторы а и b . Таким образом L и L ‘ одно и тоже векторное подпространство Þ прямые l и l ‘ совпадают.
2) На проективной плоскости «две прямые пересекаются.
Доказательство:
Р2 построено на базе V3
прямая l V2 ÌV3
прямая m V2′ ÌV3
1) V2¹V2′, так как l ¹m
2) V2ÇV2’=V1 порождает ()А; l Çm =A
так как V1ÌV2 ÞAÎl
V1ÌV2’ÞAÎm ; ()А единственная.
l и m пересекаются в единственной ()А.
3) Точки проективного пространства Р3 называются линейно зависимыми (линейно независимыми), если векторы порождающие их из пространства V4 линейно зависимы (линейно независимы).
На проективной плоскости $ три линейно независимые точки и они не лежат на одной прямой. Так как в V3 $ тройка линейно независимых векторов {e1,e2,e3}, то эта тройка на проективной плоскости порождает тройку линейно независимых точек Е1, Е2, Е3.
Покажем, что эти точки не лежат на одной прямой. Если бы эти точки принадлежали одной прямой, то вектора порождающие их должны были принадлежать V2, чего быть не может, так как эти вектора линейно независимы.
Вывод: точки Е1, Е2, Е3 не лежат на одной прямой и эти точки Е1, Е2, Е3 линейно независимы.
4) На каждой прямой лежит не менее трех точек.
Доказательство: Прямой l ÎP2 соответствует в векторном пространстве V3 двумерное подпространство V2. Пусть V2 натянуто на векторы a и b . Вектор с = a + b , с ÎV2. Соответствующие точки А,В,СÎl и различны.
Вывод: На каждой прямой лежит не менее трех точек.
Замечание : Любая четверка точек проективной плоскости линейно зависима.
1.3. Модели проективной плоскости.
1) Связка прямых в трехмерном евклидовом пространстве Е3.
Связкой прямых в Е3 называется множество прямых пространства проходящих через некоторую фиксированную ().
Эта () называется центром связки.
Пространство Е3 построено на базе V3. Зададим отображение j множества ненулевых векторов на связку по закону каждому вектору A поставим в соответствии прямую ОА связки, чтобы ОА //a .
 |
Проверим выполняемость аксиом проективной плоскости.
1)j сюрьективно, так как у » прямой ОМ всегда будет хотя бы один прообраз вектор m // ОМ
2)если 2 вектора коллинеарны a //a 1, то образы совпадают это будет прямая ОА, j(a )=j(a 1)=OA.
Если образы 2х векторов совпадают, то векторы коллинеарны.
Построенная конструкция является моделью проективной плоскости. Роль проективных точек в этой модели выполняют прямые связки, с роль проективных прямых выполняют плоскости связки.
Проанализируем, как выполняются свойства проективной плоскости.
| Свойства проективной плоскости | Реализация на модели |
|
1)Через две любые точки проходит единственная прямая 2)» две прямые на проективной плоскости пересекаются 3)$ три () не лежащие на одной прямой 4) на каждой прямой лежит не менее трех точек |
1)Через две прямые связки проходит единственная плоскость связки 2)» две плоскости связки пересекаются по прямой связки 3)$ три прямые связки не лежащие в одной плоскости связки 4)Каждой плоскости связки принадлежит не менее трех прямых этой связки |
2)Рассмотрим вторую модель расширенная евклидова плоскость.
![]()

![]()
![]()

![]() Рассмотрим в пространстве связку с центром в ()О и плоскость p не проходящую через ()О и зададим отображение j плоскости p в связку с центром в ()О по закону: «()А плоскости p ставится в соответствии прямая ОА.
Рассмотрим в пространстве связку с центром в ()О и плоскость p не проходящую через ()О и зададим отображение j плоскости p в связку с центром в ()О по закону: «()А плоскости p ставится в соответствии прямая ОА.
 |
|||
j биективно? т.е. любой ли прямой связки будет соответствовать прообраз? Ответ: нет. Прямые связки параллельные p не имеют прообразов и такие прямые называют особыми. Таких прямых будет бесчисленное множество и все они лежат в плоскости связки, которая параллельна p. Такую плоскость назовем особой плоскостью. Для того, чтобы отображение j сделать биективным и получить новую модель проективной плоскости дополним евклидову плоскость p «несобственными элементами».
Рассмотрим особую прямую связки m , m //p, и проведем через эту прямую не особую плоскость a, a(m )Çp=a , a //m .
» прямая (не особая прямая) связки Îa имеет свой прообраз на прямой a .
Поставим в соответствие прямой m не собственную ()М ¥, которая Îa .
 |
Проведем через особую прямую m другую не особую плоскость bb(m )Çp =b , a //b //m, так как каждая не особая прямая b имеет прообраз на прямую b , то прообраз особой прямой m не собственная ()М¥Îb . Если рассмотрим другую особую прямую n , то должны поставить в соответствие свою несобственную ()N¥.
Каждая не особая плоскость связки имеет на плоскости p своим прообразом прямую пересечения этой плоскости с плоскостью p.aa , bb . Поставим в соответствие особой плоскости несобственную прямую l ¥, тогда так как все особые прямые лежат в единственной особой плоскости, то все несобственные точки лежат на единственной несобственной прямой.
Определение: Расширенной евклидовой плоскостью p называется евклидова плоскость дополненная несобственными элементами: несобственными точками и единственной несобственной прямой, причем все прямые параллельные между собой дополняются одной и той же несобственной точкой и все несобственные точки лежат на единственной несобственной прямой.
Отображение j: p® связку стало биективным, так как связка прямых является моделью проективной плоскости, то и расширенная плоскость pявляется моделью проективной плоскости. Роль проективных точек в этой модели выполняют собственные и несобственные точки. Роль проективных прямых выполняют собственные прямые плоскости p и несобственная прямая.
Рассмотрим выполняемость свойств проективной плоскости на построенной модели.
| Свойства проективной плоскости | Выполнение свойств на модели |
|
1)через две любые точки проходит единственная прямая 2)» две прямые пересекаются |
1) а)()А,В собственные и через них проходит единственная прямая АВ б) А,В¥ через А проводим прямую a ¤¤b прямая АВ¥ в)А¥, В¥ лежат на единственной несобственной прямой l ¥. 2) а)a , b собственные a Çb =А б)a , b собственные но с евклидовой точки зрения ¤¤, а как прямые расширенной плоскости a Çb =А¥ в)a , b ¥ A¥ÎA, A¥Îb ¥Þ AÇb ¥=A¥ |
3)Третья модель проективной плоскости.
В трехмерном евклидовом пространстве дана сфера. Под ()М будем понимать две диаметрально противоположные точки сферы, под прямой множество пар диаметрально противоположных точек лежащих на окружности большого радиуса. Докажем, что построенное множество является проективной плоскостью. ()N=íN’,N»ý, ()K=íK’,K»ý.
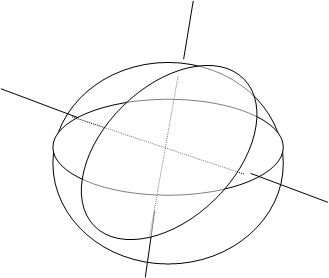 |
Рассмотрим связку с центром в ()О и зададим отображение j:A®íA’,A»ý (прямой связки соответствует пара диаметрально противоположных точек пересечения этой прямой со сферой). j биективно Þ построенная конструкция является моделью проективной плоскости.
Проверим выполняемость свойств проективной плоскости.
Свойства:
1)Через » две точки проходит единственная прямая
через две пары диаметрально противоположных точек сферы íМ’,М»ý и íN’,N»ý проходит единственная окружность большого радиуса.
2)» две прямые проективной плоскости пересекаются
» две окружности большого радиуса пересекаются в диаметрально противоположных точках.
3)$ три точки не лежащие на одной прямой
$ три пары диаметрально противоположных точек Ï одной окружности большого радиуса. Например: точки N={N’,N»},K={K’,K»},P={P’,P»}.
4)На каждой прямой лежит не менее трех точек
рассмотрим окружность большого радиуса через ()О можно провести три различных диаметра, каждый диаметр пересекает данную окружность в диаметрально противоположных точках. Это означает, что на каждой прямой лежит не менее трех точек.
1.4. Теорема Дезарга.
При данном способе построения проективной плоскости имеет место теорема Дезарга, которая гласит:
Теорема: Если прямые проходящие через соответствующие вершины двух трехвершинников пересекаются в одной точке, то точки пересечения соответствующих сторон этих трехвершинников лежат на одной прямой.
AB ÇA’B ‘=P, ACÇA’C’=Q, B CÇB ‘C’=R, AA’ÇBB ‘ÇCC’=O,
P,Q,R лежат в одной прямой?
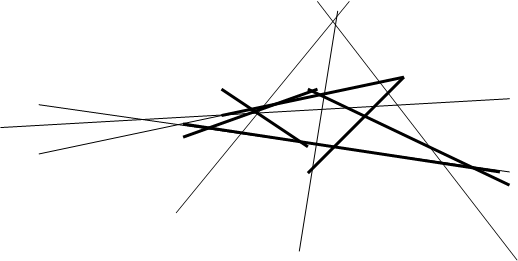
Доказательство:
Рассмотрим векторы O,A,A’,B ,B ‘,C,C’,P,Q,R порождающие соответствующие (), так как А,А’,О лежат на одной прямой, то векторы порождающие их линейно зависимы, т.е. O= a A + a ‘A’.
Из того, что В’, В, О лежат на одной прямой Þ В, В’, О линейно зависимы ÞO= bB + b ‘B ‘
()С, С’, О лежат на одной прямой ÞO= c C + c ‘C’
a A + a ‘A’ = bB + b ‘B ‘ = c C + c ‘C’
a A bB = b ‘B ‘ a ‘A’ = P (1)
А,В,Р линейно зависимы Þ () А,В,Р Î одной прямой, А’,В’,Р’ линейно зависимы Þ()А’,В’,Р’ Î одной прямой.
P=AB ÇA’B ‘
a A c C = c ‘C’ a ‘A’ (2)
А,С,Q линейно зависимы Þ()А,С,QÎ одной прямой.
А’,С’,Q’ линейно зависимы Þ()А’,С’,Q’ Î одной прямой.
Следовательно, Q=АСÇА’С’
bB c C = c’ C’ b ‘B ‘ = R (3)
В,С,R –линейно зависимы Þ()В,С,RÎ одной прямой.
В’,С’,R’ –линейно зависимы Þ()В’,С’,R’ Î одной прямой
Следовательно, R=ВСÇВ’С’.
Составим выражение: ![]()
![]() векторы
векторы ![]() линейно зависимы Þ ()P,Q,R лежат на одной прямой.
линейно зависимы Þ ()P,Q,R лежат на одной прямой.
Теорема доказана.
Принято называть трехвершинники, удовлетворяющие теореме Дезарга, дезарговыми. ()О=АА’ÇВВ’ÇСС’ дезарговой, прямую, которой принадлежат точки P,Q,R дезарговой. Для теоремы Дезарга имеет место обратная теорема:
Если точки пересечения соответственных сторон двух трехвершинников лежат на одной прямой, то прямые, проходящие через соответственные вершины этих трехвершинников, проходят через одну точку.
|

 Замечание : Трехвершинник это фигура, которая состоит из трех точек не лежащих на одной прямой и прямых проходящих через каждую пару этих точек.
Замечание : Трехвершинник это фигура, которая состоит из трех точек не лежащих на одной прямой и прямых проходящих через каждую пару этих точек.
А,В,С вершины прямые АВ,ВС,АС стороны
1.5. Теорема Паппа.
Следующей составляющей данной теории является теорема Паппа Паскаля, которая является частным случаем теоремы Паскаля. Сформулируем теорему Паскаля.
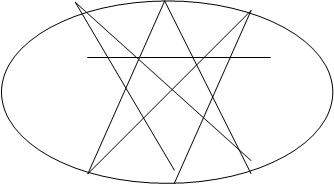 |
рис. 1
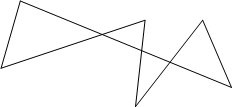
Теорема Паскаля: Для того, чтобы шесть точек, из которых никакие три не лежат на одной прямой принадлежали овальной кривой, необходимо и достаточно, чтобы точки пересечения соответствующих сторон шестивершинника* лежали на одной прямой. AB’ÇA’B=P,AC’ÇA’C=Q, BC’ÇB’C=R.(рис. 1)
P,Q,R принадлежат прямой (прямая Паскаля)
Рассмотрим теорему Паскаля в том частном случае, когда кривая второго порядка распадается на пару прямых. Пусть А,В,С,А’,В’,С’ шесть вершин шестиугольника Паскаля, расположенных по три на данных прямых l и l ‘ , которые мы рассматриваем как распавшуюся кривую второго порядка (рис 2). Тогда имеем следующие три точки пересечения пар соответствующих сторон шестиугольника: Р=АВ’ÇА’В, Q=А’СÇАС’, R=ВС’ÇВ’С. По теореме Паскаля эти три точки лежат на одной прямой. Рассмотренный частный случай теоремы Паскаля был известен древним греческим геометрам и носил название теоремы Паппа. Теперь эта теорема носит название Паппа Паскаля.
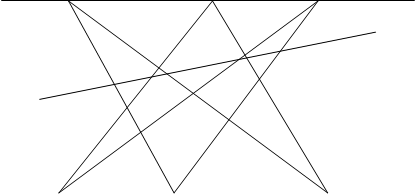 |
![]() Рис. 2
Рис. 2
![]() *шестивершинником называется фигура состоящая из последовательности шести ()А1, А2, А3, А4, А5, А6 называемых вершинами и шести прямых А1А2, А2А3, А3А4, А4А5, А5А6, А6А1 называемых сторонами.
*шестивершинником называется фигура состоящая из последовательности шести ()А1, А2, А3, А4, А5, А6 называемых вершинами и шести прямых А1А2, А2А3, А3А4, А4А5, А5А6, А6А1 называемых сторонами.
 |
 |
![]()
 |
Мы рассмотрели один из подходов к определению проективной плоскости, а именно определения проективной плоскости на базе трехмерного векторного пространства.
Теперь рассмотрим аналитическое определение проективной плоскости.
Глава 2. Аналитическое построение проективной плоскости.
2.1. Понятие проективной плоскости.
Определение 1: Проективной точкой называется класс пропорциональных троек действительных чисел, не содержащих нулевой тройки.
Будем обозначать его Х={(Х1,Х2,Х3)}
Множество всех проективных точек называется действительной проективной плоскостью.
Определение 2: Проективной прямой называется множество всех точек удовлетворяющих линейному однородному уравнению вида:
С1Х 1+ С2Х 2+ С3Х 3=0 (1)
где хотя бы одно из чисел Ci отлично от нуля.
Определение 2 корректно, так как если тройка (Х1,Х2,Х3) удовлетворяет уравнению (1), то в силу его однородности при любом действительном l тройка (lХ1, lХ2, lХ3) удовлетворяет уравнению (1).
Точки, удовлетворяющие уравнению (1) удовлетворяют также линейному однородному уравнению.
(mС1)Х 1+ (mС2)Х 2+ (mС3)Х 3=0 (2)
при «mÎR: m¹0.
Поэтому каждой прямой, заданной уравнением (2) можно поставить во взаимно однозначное соответствие класс пропорциональных троек С={(С1,С2,С3)}. Так, что тройками из одного класса соответствует одна прямая, причем этот класс не содержит нулевой тройки. Ввиду этого прямую, заданную уравнением (2) будем обозначать той же буквой С, что и соответствующий класс {(С1,С2,С3)}.
Равенство (2) можно записать также в виде
СХ=0 (3)
Скалярное произведение троек С и Х. СХ= C1Х1 + С2Х2 + С3Х3 =0
Замечание : Рассмотрим 3мерное линейное пространство L3. Исключим из него нулевой вектор 0. Множество L3\{0} разобьем по классам эквивалентности так, что векторы одного класса коллинеарны между собой. Каждый такой класс назовем проективной точкой, а множество всех классов 2мерным проективным пространством (плоскостью). Множество всех классов, векторы которых принадлежат \{0} назовем одномерной проективной плоскостью (прямой).
В L3 введем координаты. Тогда каждому вектору соответствует строка (Х1,Х2,Х3), а каждому классу эквивалентности из L3\{0} (т.е. проективной ()) класс {(Х1,Х2,Х3)} пропорциональных строк, не содержащий нулевой строки.
Мы пришли к определению проективной плоскости.
2.2. Свойства проективной плоскости.
Докажем несколько простых теорем о взаимном расположении () и прямых на проективной плоскости.
Теорема 1: Через две различные () проходит единственная прямая.
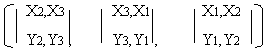 Доказательство: 1) Существование. Пусть Х= {(Х1,Х2,Х3)} и У={(Y1,Y2,Y3)} две различные (). Определим прямую следующим образом:
Доказательство: 1) Существование. Пусть Х= {(Х1,Х2,Х3)} и У={(Y1,Y2,Y3)} две различные (). Определим прямую следующим образом:
C= Х*Y то есть С =
так как CХ = (Х*Y)Х = |Х,Y,Х| = 0
CY = (Х*Y)Y = |Х,Y,Y| = 0
и по свойству определителей, то () Х и Y принадлежат прямой С.
2) Единственность. Если прямая С={(C1,C2,C3)} содержит () Х и Y, то любой представитель (C1,C2,C3) класса С удовлетворяет системе уравнений.
![]() C1Х1 + C2Х2 + C3Х3 =0
C1Х1 + C2Х2 + C3Х3 =0
C1Y1 + C2Y2 + C3Y3 =0 (5)
$ бесконечное множество ненулевых решений этой системы (нулевое решение не определяет прямую). При этом для » решения (С1,С2,С3) справедливо равенство:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Y2,Y3 , Y3,Y1 , Y1,Y2
Т.е. решения системы (5) образуют единственный класс ненулевых троек. Этот класс определяет единственную прямую С. ч.т.д.
Теорема 2: Две различные прямые имеют единственную общую точку.
Доказательство: Пусть, С={(С1,С2,С3)}, m={(m 1,m 2,m 3)} две различные прямые. Найдем () Х ={(Х1,Х2,Х3)}, лежащую на этих прямых. Достаточно повторить доказательство предыдущей теоремы, заменив Х на С, Y на m , С на Х. Получим, что единственная общая точка Х определяется равенством
Х=С*m (6). ч.т.д.
Теорема 3: Для того, чтобы три () Х,Y,Z лежали на одной прямой, необходимо и достаточно, чтобы
![]()
![]()
![]()
![]()
|X,Y,Z|=0 (7), то есть Y1 Y2 Y3 =0
Z1 Z2 Z3
Доказательство: 1)Необходимость. Пусть () X,Y,Z лежат на одной прямой С. если хотя бы две из них совпадают, то равенство (7) следует из определения смешенного произведения и свойств определителя. Пусть эти () различны. Пользуясь теоремой 1, можно записать C=X*Y. Так как ()Z лежит на прямой C, то CZ=0 Þ (X*Y)Z=|X,Y,Z|=0
2)Достаточность. Пусть выполняется равенство (7). Рассмотрим произведение C=X*Y. Равенство (7) можно записать в виде (X*Y)Z=0, то есть CZ=0 Þ()z лежит на прямой C проходящей через () X и Y. Равенство (7) не зависит от выбора представителей точек.
Теорема доказана.
Теорема 4: Для того, чтобы три прямые c, m, n проходили через одну () необходимо и достаточно, чтобы
|c,m,n|=0 (8)
Для троек действительных чисел понятие линейной зависимости и линейной независимости определяется так же, как и для векторов. Пусть тройки x,…, x линейно зависимы. Легко проверить, что » другие тройки x,…, x, принадлежащие тем же классам, тоже линейно зависимы. Поэтому классы троек (точки) линейно зависимы, если линейно зависимы какиенибудь представители этих классов.
Из теорем 3 и 4 следуют две теоремы.
Теорема 5: Для того, чтобы три () лежали на одной прямой, необходимо и достаточно, чтобы они были линейно зависимы.
Теорема 6: Для того, чтобы три прямые проходили через одну (), необходимо и достаточно, чтобы они были линейно зависимы.
2.3. Теорема Дезарга.
На проективной действительной плоскости имеет место теорема Дезарга.
Теорема Дезарга : Если прямые проходящие через соответствующие вершины двух трехвершинников пересекаются в одной точке, то точки пересечения соответствующих сторон этих трехвершинников лежат на одной прямой.
P=ABÇA’B’, Q=ACÇA’C’, R=BCÇB’C’, AA’ÇBB’ÇCC’=Q
P,Q,R лежат на одной прямой.
![]()
![]()
![]()
![]()




  |
А(1,0,0), В(0,1,0), С(0,0,1), О(1,1,1)
Координаты ()А’ есть линейная комбинация координат ()А и ()О, так как А¹А’, то а’=aА + dq
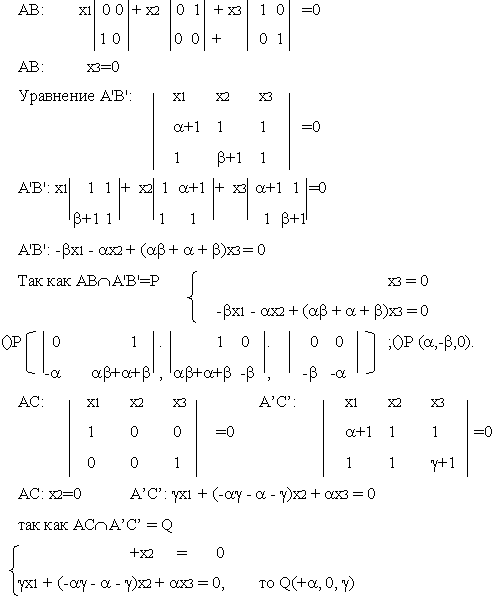  |
Можно положить d=1. Тогда получаем А’=aА +q. Тоже самое относится и к другим вершинам трехвершинника A’B’C’. Поэтому А'(a+1,1,1), В'(1,b+1,1), С'(1,1,g+1) уравнение прямой АВ:
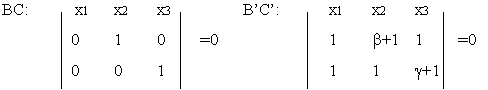
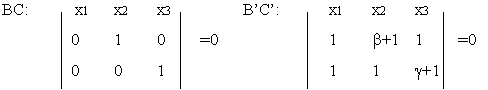
так как R= BCÇB’C’
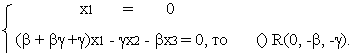
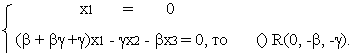
С помощью условия коллинеарности трех () убедимся, что () P,Q,R лежат на одной прямой.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
a 0 g = a b 0 =0
0 b g 0 b g
Условие коллинеарности выполнено, следовательно, P,Q,RÎ одной прямой.
Теорема доказана.
Глава 3. Аксиоматическое построение проективной плоскости.
3.1. Аксиоматика аффинной плоскости.
Начнем с некоторых наиболее простых фактов обычной плоской геометрии, которые мы применим в качестве аксиом при синтетическом построении теории.
Определение : Аффинной плоскостью называют множество элементов, именуемых точками и систему его подмножеств, именуемых прямыми, причем должны выполнятся три формулируемые ниже аксиомы А1А3.
А1: Для » двух различных точек Р и Q$ единственная прямая, проходящая через них.
Две прямые называются параллельными, если они совпадают или не имеют общих точек.
А2: Для » заданной прямой l и точки Р $ одна и только одна проходящая через Р прямая m : m || l
А3: $ три неколлинеарные точки (Точки Р1,Р2,…Рn называются коллинеарными, если $ прямая l , что все эти точки ей принадлежат).
Пример: Евклидова плоскость Е2 удовлетворяет аксиомам А1А3, то есть является аффинной плоскостью.
Пример: Аффинная плоскость имеет, по крайней мере, четыре различных точки; плоскость состоящая ровно из четырех () существует.
Действительно в силу А3 на плоскости есть три неколлинеарные точки; обозначим их через P ,Q,R. Согласно А2, $ прямая l , проходящая через Р и параллельной прямой QR, соединяющей Q и R (эта прямая $ по А1). Точно так же доказывается $ прямой
m || P Q, проходящей через R.
Покажем теперь, что l || m .
же S¹R. Таким образом, четвертая () S необходимо должна существовать и наше первое утверждение доказано.
  |
Теперь рассмотрим прямые P R и QS. Они могут пересекаться, но они могут и не пересекаться это не противоречит аксиомам.
В этом случае мы получаем аффинную плоскость, содержащую ровно четыре () P ,Q,R,S и шесть прямых P Q,РR,P S,QR,QS,RS.
Аксиомы А1А3 здесь выполняются, таким образом, мы получим аффинную плоскость ![]()
![]()
3.2. Аксиоматика проективной плоскости.
Определение : Проективной плоскостью S называют множество, элементами которого именуются точками, и набор его подмножеств, именуемых прямыми, если при этом выполняются следующие четыре аксиомы.
П1.Через две различные точки P и Q плоскости S можно провести единственную прямую.
П2. » две прямые пересекаются по меньшей мере в одной точки.
П3. $ три неколлинеарные точки.
П4. Прямая содержит, по меньшей мере, три точки.
3.3. Модели проективной плоскости.
1)Рассмотренная ранее расширенная евклидовая плоскость есть модель проективной плоскости.
Доказательство: Проверим выполнение четырех аксиом П1П4.
П1. Пусть P и QÎ![]()
![]()
1. Если Р и Q собственные (), то через них можно провести только одну прямую.
2. Если Р собственная точка p, а Q несобственная точка, то по аксиоме А2 $ прямая m , такая, что РÎm и m || l , так , что QÎ пополнению прямой m до прямой из p. Прямая m единственная прямая p, проходящая через Р и Q.
3. Если Р и Q несобственные (), то через них проходит единственная несобственная прямая.
П2. Пусть заданы прямые l и m .
1.Если l и m несобственные прямые и l || m , то они пересекаются в некоторой точке. Если l || m , то они пересекаются в несобственной точке Р¥.
2.Если l собственная прямая, а m несобственная прямая, то они пересекаются в несобственной точке Р¥.
П3. Непосредственно следует из А3. Необходимо только проверить, что если Р и Q и R неколлинеарны в А, то они не будут коллинеарны в p. Действительно, в p$ только одна (несобсвтенная) прямая, не принадлежащая А, но () Р,Q,R ей не принадлежат.
П4. Каждая прямая плоскости А содержит хотя бы две (). Но в p каждая прямая содержит еще и несобственную точку, поэтому она содержит не менее трех точек.
2) Пополняя аффинную плоскость А из четырех (), мы получим проективную плоскость S1 из семи точек.
Докажем это: Проверим выполнение четырех аксиом П1П4.
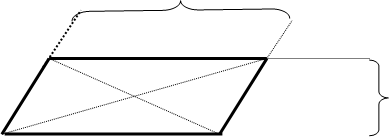  |
||
Определим () пересечения прямых АВÇCD=N ¥, BCÇAD=M ¥, АCÇBC=P ¥N ¥, P ¥, M ¥Î одной несобственной прямой.
П1. Через две различные () плоскости можно провести единственную прямую.
Если А,В собственные (), то через них можно провести только одну прямую из А. () А,В Î несобственной прямой, поэтому и в S1 через них можно провести единственную прямую.
Рассмотрим А собственная () и N ¥ несобственная (). Через эти точки проходит единственная прямая, так как () N ¥ определена как пересечение прямых АВ и CDÞN ¥ÎАВ.
Пусть имеем не собственные точки, через них проходит несобственная прямая S1 и она единственная.
П2. » две прямые пересекаются по меньшей мере в одной точке.
Справедливость аксиомы П2 следует из определения S1.
П3. $ три неколлинеарные точки.
Непосредственно следует из построения аффинной плоскости А. А мы дополнили точками N ¥, P ¥, M ¥ (несобственными, которые принадлежат одной несобственной прямой). И поэтому точки не коллинеарные в А будут неколлинеарные в S1.
П4. Каждая прямая плоскости А содержит хотя бы две точки. В S1 каждая прямая содержит несобственную точку. Следовательно прямая в S1 содержит не менее трех точек.
Все аксиомы проективной плоскости выполняются, следовательно, S1 проективная плоскость.
3) Связка прямых евклидова трехмерного пространства модель проективной плоскости, построенной на аксиомах П1П4.
3) Действительная проективная плоскость (множество упорядоченных троек действительных чисел, одновременно не равных нулю), рассмотренная ранее, удовлетворяет аксиомам П1П4.
3.4. Теорема Дезарга.
Одним из важных результатов проективной геометрии является теорема Дезарга, которая утверждает следующее:
П5 (теорема Дезарга)


  |
P =ABÇA’B’ AA’ÇBB’ÇCC’=0
Q=ACÇA’C’
R=BCÇB’C’
P ,Q,R лежат на одной прямой.
В рамках теории, которую мы строим, не совсем правильно называть это утверждение “теоремой”, потому что нельзя доказать, исходя только из аксиом П1П4. Примем это утверждение за аксиому П5. Хотя при первом и втором способе построения проективной плоскости это утверждение выступает как теорема.
Покажем, что П5 не есть следствие П1П4, а именно, построим геометрию, удовлетворяющую аксиомам П1П4, но не удовлетворяющую П5.
Определение : Конфигурацией называют множество элементов, именуемых точками, и набор его подмножеств, именуемых прямыми, если при этом выполняется аксиома.
К1. Две различные () принадлежат не более чем одной прямой.
Отсюда следует, что две различные прямые имеют не более одной общей точки
Примеры: Любая аффинная и » проективная плоскость являются конфигурациями. Набор 10 точек и 10 прямых теоремы Дезарга тоже конфигурация.
Пусть p0 некоторая конфигурация. Мы определим свободную проективную плоскость П, порожденную p0.
Пусть p1 новая конфигурация, определенная следующим образом. Точками p1 являются точки p0. Прямыми p1 являются все прямые p0; кроме того, каждая пара точек Р1, Р2Îp0 не принадлежащая прямой из p0, задает новую прямую
í Р1, Р2ý из p1. Тогда p1 обладает следующим свойством;

 (6 оценок, среднее: 4,67 из 5)
(6 оценок, среднее: 4,67 из 5)