Учебная работа № 1952. Курс лекций по теории вероятностей
Раздел 1. Классическая вероятностная схема
1.1 Основные формулы комбинаторики
В данном разделе мы займемся подсчетом числа «шансов». О числе шансов говорят, когда возможно несколько различных результатов какоголибо действия (извлечение карты из колоды, подбрасывание кубика или монетки, двух кубиков и т.д.). Число шансов — это число таких возможных результатов, или, иначе говоря, число способов проделать это действие.
Теорема о перемножении шансов
Теорема 1 . Пусть имеется, k групп элементов, причем i я группа содержит ni элементов, 1<= i <= k . Выберем из каждой группы по одному элементу. Тогда общее число N способов, которыми можно произвести такой выбор, равняется
![]()
Замечание 1 . В теореме 1 считается, что даже если все элементы в i й группе неразличимы, выбрать один из них можно ni способами.
Замечание 2. Результат выбора, описанного в теореме 1 , представим в виде набора (а1 , а 2 ,…, а k ) в котором а i — выбранный из i й группы элемент. Тогда общее число различных наборов (а1 , а 2 ,…, а k ) также равняется
![]()
![]()
![]()
Доказательство теоремы 1.


Но столько же пар можно составить и с любым другим элементом первой группы. Тогда всего пар, в которых первый элемент выбран из первой группы, а второй — из второй, существует ровно ![]()
![]()
![]()
Иначе говоря, есть ![]()
![]()
![]()
Но столько же троек можно составить и с любой другой парой ( j , l ). Тогда всего троек, в которых первый элемент выбран из первой группы, второй — из второй, а третий — из третьей, существует ровно ![]()
![]()
Продолжая рассуждения, методом математической индукции заключаем справедливость утверждения теоремы.
Урны и шарики
Есть урна, (то есть ящик), содержащая n занумерованных объектов, которые мы без ограничения общности будем считать шариками. Мы выбираем из этой урны k шариков. Нас интересует, сколькими способами можно выбрать k шариков из n , или сколько различных результатов (то есть наборов, состоящих из k шариков) получится.
На этот вопрос нельзя дать однозначный ответ, пока мы не определимся
· с тем, как организован выбор (скажем, можно ли шарики возвращать в урну), и
· с тем, что понимается под различными результатами выбора.
Рассмотрим следующие возможные схемы выбора:
1. Выбор с возвращением: каждый выбранный шарик возвращается в урну, то есть каждый из k шариков выбирается из полной урны. В полученном наборе, состоящем из k номеров шариков, могут встречаться одни и те же номера (выборка с повторениями ).
2. Выбор без возвращения: выбранные шарики в урну не возвращаются, и в полученном наборе не могут встречаться одни и те же номера (выборка без повторений ).
И в том, и в другом случае результатом выбора является набор из k номеров шариков. Удобно считать, что шарики всегда выбираются последовательно, по одному (с возвращением или без).
Условимся, какие результаты мы будем считать различными .
Есть ровно две возможности.
1. Выбор с учетом порядка: два набора номеров шариков считаются различными, если они отличаются составом или порядком номеров. Так, при выборе трех шариков из урны, содержащей 5 шариков, наборы (1,2,5), (2,5,1) (4,4,5) различны, если производится выбор с учетом порядка.
2. Выбор без учета порядка: два набора номеров шариков считаются различными, если они отличаются составом. Наборы, отличающиеся лишь порядком следования номеров, считаются одинаковыми. Так, в примере выше первые два набора (1,2,5), (2,5,1) есть один и тот же результат выбора, а набор (4,4,5) — другой результат выбора.
Подсчитаем теперь, сколько же возможно различных результатов при каждой из четырех схем (выбор с возвращением и без, и в каждом из этих случаев учитываем ли мы порядок или нет).
Урновая схема: выбор без возвращения, с учетом порядка
Теорема 2 . Общее количество выборок в схеме выбора k элементов из n без возвращения и с учетом порядка определяется формулой
и называется числом размещений из n элементов по k элементов .
Доказательство . Первый шарик можно выбрать n способами. При каждом из этих способов второй шарик можно выбрать n 1 способом, и т.д. Последний k й шарик можно выбрать ( n k +1) способом. По теореме 1 , общее число способов выбора равно
![]()
![]()
что и требовалось доказать.
Следствие 1. Число возможных перестановок множества из n элементов есть n !
Доказательство очевидно, если заметить, что перестановка есть не что иное, как результат выбора без возвращения и с учетом порядка всех n элементов из n . Так что общее число перестановок равно
Урновая схема: выбор без возвращения и без учета порядка
Теорема 3. Общее количество выборок в схеме выбора k элементов из n без возвращения и без учета порядка определяется формулой
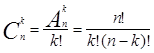 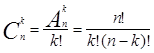 |
и называется числом сочетаний из n элементов по k элементов .
Доказательство . Заметим, что, согласно следствию 1 , из каждой выборки данного состава (состоящей из k элементов) можно образовать k ! выборок, отличающихся друг от друга только порядком элементов.
То есть число выборок, различающихся еще и порядком, в k ! раз больше, чем число выборок, различающихся только составом. Поделив ![]()
![]()
Урновая схема: выбор с возвращением и с учетом порядка
Теорема 4 . Общее количество выборок в схеме выбора k элементов из n с возвращением и с учетом порядка определяется формулой
Доказательство . Первый шарик можно выбрать n способами. При каждом из этих способов второй шарик можно выбрать также n способами, и так k раз.
Урновая схема: выбор с возвращением и без учета порядка
Рассмотрим урну с двумя шариками и перечислим результаты выбора двух шариков из этой урны при выборе с возвращением:
| С учетом порядка | Без учета порядка |
|
(1, 1) (2, 2) (1, 2) (2, 1) |
(1, 1) (2, 2) (1, 2) |
Заметим, что в схеме «без учета порядка» получилось 3 различных результата в отличие от четырех в схеме «с учетом порядка». (число 4 возникает и согласно теореме 4 ); и что никаким делением на «число какихнибудь перестановок» число 3 из 4 получить не удастся.
Теорема 5 . Общее количество выборок в схеме выбора k элементов из n с возвращением и без учета порядка определяется формулой
Доказательство . Рассмотрим подробно, чем отличаются друг от друга два разных результата такой схемы выбора. Нам не важен порядок номеров, то есть мы учитываем только, сколько раз в нашем наборе из k номеров шариков появился шарик номер 1, шарик номер 2, … , шарик номер n . То есть результат выбора можно представить набором чисел k 1 , k 2 , … kn , в котором ki — число появлений шарика номер i в выборке, и k 1 + k 2 + …+ kn .= k . При этом два результата эксперимента различны, если соответствующие им наборы k 1 , k 2 , …, kn не совпадают.
Представим себе другой эксперимент, имеющий точно такие же результаты (и, следовательно, их столько же). Есть n ящиков, в которых размещается k шариков. Нас интересует только количество шариков в каждом ящике. То есть, результатом эксперимента снова является набор чисел k 1 , k 2 , … kn , в котором ki — число шариков в ящике с номером i , и k 1 + k 2 + … + kn .= k . Числа ki попрежнему принимают натуральные значения или равны 0.
А теперь изобразим результат такого размещения в виде схемы, в которой вертикальные линии обозначают перегородки между ящиками, а кружки — находящиеся в ящиках шарики:
Мы видим результат размещения 9 шариков по 7 ящикам. Здесь 1й ящик содержит 3 шарика, 2й и 6й ящики пусты, 3й ящик содержит 1 шарик, и в 4м и 5м ящиках есть по 2 шарика. Переложим один шарик из первого ящика во второй и изобразим таким же образом еще один результат размещения:
![]()
![]()
И еще один:
Видим, что все размещения можно получить, меняя между собой шарики и перегородки, или расставляя k шариков на n 1+ k месте. Число n 1+ k получается так: у n ящиков есть ровно n +1 перегородка, считая крайние, или n 1 перегородка, если не считать крайние, которые двигать нельзя. И есть k шариков. Перебрав все возможные способы расставить k шариков на этих n 1+ k местах (и ставя на оставшиеся места перегородки), переберем все нужные размещения.
Но способов расставить k шариков на n 1+ k местах ровно ![]()
![]()
![]()
![]()
1.2 Основные понятия элементарной теории вероятностей
Предмет теории вероятностей. Статистическая устойчивость.
Теория вероятностей изучает закономерности, возникающие в случайных экспериментах (явлениях). Случайным называют эксперимент, результат которого нельзя предсказать заранее. Невозможность предсказать заранее — основное, что отличает случайное явление от детерминированного .
Не все случайные явления (эксперименты) можно изучать методами теории вероятностей, а лишь те, которые могут быть воспроизведены в одних и тех же условиях и обладают (непонятно как проверяемым заранее) свойством «статистической устойчивости : «если А — некоторое событие, могущее произойти или не произойти в результате эксперимента, то доля n ( A )/ n числа экспериментов, в которых данное событие произошло, имеет тенденцию стабилизироваться с ростом общего числа экспериментов n , приближаясь к некоторому числу P ( A ) . Это число служит объективной характеристикой «степени возможности» событию А произойти.
В дальнейшем мы будем говорить лишь о случайных экспериментах, обладающих данными свойствами, а свойство статистической устойчивости докажем в утверждении, известном как закон больших чисел Я.Бернулли.
Пространство элементарных исходов. Операции над событиями
Определение 1 . Пространством элементарных исходов Ω («омега») называется множество, содержащее все возможные результаты данного случайного эксперимента, из которых в эксперименте происходит ровно один. Элементы этого множества называют элементарными исходами и обозначают буквой ω («омега») с индексами или без.
Определение 2 . Событиями мы будем называть подмножества множества Ω . Говорят, что в результате эксперимента произошло событие А Í Ω , если в эксперименте произошел один из элементарных исходов, входящих в множество А .
Замечание 3 . Вообще говоря, можно назвать событиями не обязательно все подмножества множества Ω , а лишь множества из некоторого набора подмножеств. О смысле такого ограничения мы поговорим позднее.
Пример 1 . Один раз подбрасывается одна игральная кость (кубик). Самый разумный способ задать пространство элементарных исходов таков: Ω = {1,2,3,4,5,6} , элементарные исходы здесь соответствуют числу выпавших очков.
Примеры событий: A = {1,2} — выпало одно или два очка; A = {1,3,5} — выпало нечетное число очков.
Пример 2 . Два раза подбрасывается одна игральная кость (кубик). Или, что, то же самое, один раз подбрасываются две игральные кости. Как мы увидим в дальнейшем, здесь самый разумный способ задать пространство элементарных исходов — считать результатом эксперимента упорядоченную пару чисел (i, j), в которой 1 £ i, j £ 6 и i число очков выпавших первый раз, j – число очков, выпавших второй раз. Ω = {(i, j) , где 1 £ i, j £ 6}
Примеры событий:
A = {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6)} — при первом подбрасывании выпало одно очко;
A = {(1,1),(2,2), (3,3), (4,4), (5,5), (6,6)} — при двух подбрасываниях выпало одинаковое число очков.
Пример 3 . На поверхность стола бросается монета. Результатом эксперимента можно считать координату центра монеты (а если нам не безразличен угол поворота монеты, то можно добавить и величину этого угла). Пространство элементарных исходов — множество точек стола (во втором случае — множество пар {x, φ} , где x — координата точки стола и φ Î[0, 2 π ] — угол поворота). Число элементарных исходов такого эксперимента несчетно.
Пример 4 . Монета подбрасывается до тех пор, пока не выпадет вверх гербом. Пространство элементарных исходов состоит из бесконечного, но счетного числа исходов:
Ω = {г, рг, ррг, рррг, ррррг, рррррг, …} , где р и г обозначают выпадение решки и герба при одном подбрасывании, соответственно.
Пример 5 . Приведем пример неправильно выбранного пространства элементарных событий. Пусть при бросания игральной кости Ч = {четное число очков}, Т = {число очков, кратное трем}. Тогда Ω = {Ч, Т, 1, 5} составляет все исходы эксперимента, однако исходы Ч и Т могут наступать одновременно.
Определение 3 .
1. Достоверным называется событие, которое обязательно происходит в результате эксперимента, то есть единственное событие, включающее все без исключения элементарные исходы — событие Ω .
2. Невозможным называется событие которое не может произойти в результате эксперимента, то есть событие, не содержащее ни одного элементарного исхода («пустое множество» Æ). Заметим, что всегда ÆÎΩ .
Определение 4 . Пусть А иВ — события.
1. Объединением А U В событий А иВ называется событие, состоящее в том, что произошло либо А , либо В , либо оба события одновременно. На языке теории множеств А U В есть множество, содержащее как элементарные исходы, входящие в А , так и элементарные исходы, входящие в В .
2. Пересечением А ∩ В событий А иВ называется событие, состоящее в том, что произошли оба события А иВ одновременно. То есть А ∩ В есть множество, содержащее элементарные исходы, входящие одновременно в А и в В .
3. Дополнением А \ В события А доВ называется событие, состоящее в том, что произошло событие А , но не произошло В . То есть А \ В есть множество, содержащее элементарные исходы, входящие в А , но не входящие в В .
4. Противоположным (или дополнительным ) к событию А называется событие ![]()
![]()
![]()
![]()
Определение 5 .
1. События А иВ называются несовместными , если А ∩ В = Æ.
2. События А1 , А2 , … А n называются попарно несовместными , если для любых i ≠ j , 1 £i , j £n , события А i и А j несовместны.
3. Говорят, что событие А влечет событие В , и пишут А ÍВ , если всегда, как только происходит событие А , происходит и событие В . На языке теории множеств это означает, что любой элементарный исход, входящий в А , одновременно входит и в событие В .
Вероятность на дискретном пространстве элементарных исходов
Предположим, что мы имеем дело с дискретным пространством элементарных исходов, то есть пространством, состоящим из конечного или счетного числа элементов:
Ω = {ω1, ω2 , … ω n , … }.
Определение 6. Поставим каждому элементарному исходу ω i ÎΩ в соответствие число p (ω i ) Î [0,1] так, что
Назовем число p (ω i ) вероятностью элементарного исхода ω i . Вероятностью события А Í Ω называется число
равное сумме вероятностей элементарных исходов, входящих в множество А .
Замечание 4 . Позднее, познакомившись с аксиоматикой теории вероятностей, мы зададим вероятности событий непосредственно, а не через вероятности элементарных исходов. Тем более, что сложением вероятностей элементарных исходов можно получить лишь вероятность события, состоящего не более чем из счетного числа элементарных исходов (иначе само понятие суммирования не определено). Но на дискретном пространстве элементарных исходов определить вероятности событий так, как это сделано в определении 6, всегда возможно.
Перечислим очевидные в случае дискретного пространства элементарных исходов свойства вероятности, которые мы скоро докажем сразу в общем случае.
1. 0 £ Р(А) £ 1 ;
2. Р( Ω) = 1 ;
3. Р( Æ) = 0 ;
4. Р( Ō) = 1 Р( О) ;
5. если А иВ несовместны, то Р(А U В) = Р(А) + Р(В) ;
6. в общем же случае Р(А U В) = Р(А) + Р(В) Р(А ∩ В) ;
7. если А Í В , то Р(А) £ Р(В) .
Классическое определение вероятности
Предположим, что мы имеем дело с пространством элементарных исходов, состоящим из конечного числа N элементов: Ω = {ω1, ω2 , … ω N } . Более того, предположим, что из какихлибо соображений мы можем считать элементарные исходы равновозможными. Тогда вероятность любого из них принимается равной 1/ N .
Эти соображения чаще всего не имеют отношения к математической модели и основаны на какойлибо симметрии в эксперименте (симметричная монета, хорошо перемешанная колода карт, правильная кость). Либо мы можем заранее считать исходы эксперимента равновозможными, но тогда рано или поздно все равно возникнет вопрос о соответствии такой математической модели реальному эксперименту.
Если событие А = { ![]()
![]()

 (6 оценок, среднее: 4,67 из 5)
(6 оценок, среднее: 4,67 из 5)