Учебная работа № 1842. Три кризиса в развитии математики

Учебная работа № 1842. Три кризиса в развитии математики

ÐÅÖÅÍÇÈß

íà äèïëîìíóþ ðàáîòó ñòóäåíòà V êóðñà
ôèçèêîìàòåìàòè÷åñêîãî ôàêóëüòåòà ÀÃÏÈ

Áîëüøàêîâà À. À. íà òåìó:
“Òðè êðèçèñà â ðàçâèòèè ìàòåìàòèêè”

Ðàçâèòèå ìàòåìàòèêè íå îäíàæäû ïðèâîäèëî â ïðîøëîì ê íåîáõîäèìîñòè îñìûñëåíèÿ è ïåðåñòðîéêè å¸ îñíîâ. Äèïëîìíàÿ ðàáîòà Áîëüøàêîâà À. À. ïîñâÿùåíà îáçîðó òðåõ ïåðèîäîâ èíòåíñèâíûõ ïîèñêîâ ïóòåé ïðåîäîëåíèÿ íàêîïèâøèõñÿ âíóòðåííèõ ïðîòèâîðå÷èé: àíòè÷íûé ïåðèîä, ïåðèîä îáîñíîâàíèÿ àíàëèçà è òåîðåòèêîìíîæåñòâåííûé ïåðèîä.

 ðàáîòå ïðèâîäèòñÿ ìíîãî èíòåðåñíûõ èñòîðè÷åñêèõ ñâåäåíèé. Ïîêàçàíû íåïðîñòûå ïóòè ôîðìèðîâàíèÿ íåêîòîðûõ îñíîâíûõ ìàòåìàòè÷åñêèõ ïîíÿòèé.

Àâòîð ïîêàçûâàåò ãëóáîêîå ïðîíèêíîâåíèå â òåìó è õîðîøåå âëàäåíèå ìàòåðèàëîì. Äèïëîìíàÿ ðàáîòà Áîëüøàêîâà À. À. çàñëóæèâàåò âûñîêîé îöåíêè.

Çàâåäóþùèé êàôåäðîé

ìàòåìàòè÷åñêîãî àíàëèçà,

êàíäèäàò ôèçèêîìàòåìàòè÷åñêèõ
íàóê

Çàõàðîâ Ñ. À.

Ìèíèñòåðñòâî îáðàçîâàíèÿ Ðîññèéñêîé Ôåäåðàöèè

Àñòðàõàíñêèé ïåäàãîãè÷åñêèé èíñòèòóò èì. Ñ. Ì. Êèðîâà

Òðè êðèçèñà
â ðàçâèòèè ìàòåìàòèêè

ÄÈÏËÎÌÍÀß ÐÀÁÎÒÀ

студента физикоматематического
факультета

Научный руководитель
Ованесов Н. Г.

Àñòðàõàíü · 96

Îãëàâëåíèå

Ââåäåíèå

I. Ñïîñîáû îáîñíîâàíèÿ ìàòåìàòèêè â äðåâíåé Ãðåöèè îò Ïèôàãîðà äî Åâêëèäà.

1. Ìàòåìàòèêà ïèôàãîðåéöåâ

2. Ïðîáëåìà áåñêîíå÷íîñòè â äðåâíåãðå÷åñêîé ôèëîñîôèè è ìàòåìàòèêå

3. Òðè çíàìåíèòûõ çàäà÷è äðåâíîñòè

4. Ïðåîäîëåíèå êðèçèñà îñíîâ äðåâíåãðå÷åñêîé ìàòåìàòèêè

II. Ñïîñîáû îáîñíîâàíèÿ ìàòåìàòèêè â XVIII è â ïåðâîé ïîëîâèíå XIX âåêà

1. Îñîáåííîñòè ñïîñîáîâ îáîñíîâàíèÿ ìàòåìàòèêè â êîíöå XVII è â XVIII âåêå

2. Ðàçðàáîòêà ñïîñîáîâ îáîñíîâàíèÿ ìàòåìàòèêè â ïîñëåäíåé ÷åòâåðòè XVIII è ïåðâîé ïîëîâèíå XIX âåêà

III. Ñïîñîáû îáîñíîâàíèÿ ìàòåìàòèêè â ïîñëåäíåé ÷åòâåðòè XIX âåêà è íà÷àëà XX âåêà

1. Òåîðèÿ ìíîæåñòâ. Îñíîâíûå ïîíÿòèÿ ó÷åíèÿ î ìíîæåñòâàõ Ã. Êàíòîðà

2. Òðóäíîñòè ïîñòðîåíèÿ òåîðèè ìíîæåñòâ. Êðèòèêà êîíöåïöèè Ã. Êàíòîðà

3. Ïàðàäîêñû (àíòèíîìèè) òåîðèè ìíîæåñòâ

4. Àêñèîìàòè÷åñêèå ïîñòðîåíèÿ òåîðèè ìíîæåñòâ ïî Öåðìåëî

5. Ïðîáëåìà ñóùåñòâîâàíèÿ â ìàòåìàòèêå

Ñïèñîê ëèòåðàòóðû.

Ñîçäàíèå íîâûõ è äàëüíåéøåå ðàçâèòèå ñóùåñòâóþùèõ ìàòåìàòè÷åñêèõ òåîðèé ñâÿçàíî îáû÷íî ñ óòî÷íåíèåì (îáîáùå­íèåì) èõ èñõîäíûõ îñíîâíûõ ïîíÿòèé è ïîñûëîê è îñíîâàííûõ íà íèõ ìåòîäîâ. Ìàòåìàòèêè íåðåäêî âñòðå÷àëèñü ñ òðóäíîñòÿìè, ïðåîäîëåòü êîòîðûå èì óäàâàëîñü òîëüêî ïîñëå ïðîäîëæèòåëüíûõ ïîèñêîâ. Ýòè òðóäíîñòè ðîñòà ìàòåìàòèêè — òðóäíîñòè å¸ îáîñíîâàíèÿ: îíè áûëè, åñòü è áóäóò â äàëüíåéøåì.

Òðóäíîñòè îáîñíîâàíèÿ ìàòåìàòèêè èãðàþò íàèáîëåå çíà÷èòåëüíóþ ðîëü â ðàçâèòèè ìàòåìàòèêè òîãäà, êîãäà âîçíèêàåò íåîáõîäèìîñòü â êîðåííîé ïåðåðàáîòêå îñíîâ è ìåòîäîëîãèè âñåõ (èëè äîñòàòî÷íî áîëüøîãî ÷èñëà) ìàòåìàòè÷åñêèõ òåîðèé.  ýòèõ ñëó÷àÿõ ãîâîðÿò î êðèçèñå îñíîâ ìàòåìàòèêè. Èçâåñòíû òðè òàêèõ êðèçèñà.

Âïåðâûå êðèçèñ îñíîâ íàóê âîçíèê â ìàòåìàòèêå â äðåâíåé Ãðåöèè, â íà÷àëå å¸ ôîðìèðîâàíèÿ êàê íàó÷íîé ñèñòåìû. Âòîðîé èìåë ìåñòî â êîíöå XVII è â XVIII âåêå. Òðåòèé âîçíèê â êîíöå XIX âåêà, îí íå ïðåîäîëåí è â íàøå âðåìÿ è îêàçûâàåò âëèÿíèå íà ðàçâèòèå ñîâðåìåííîé ìàòåìàòèêè.

Ìû ðàññìîòðèì ñóùíîñòü ýòèõ êðèçèñîâ ìàòåìàòèêè, èìåÿ â âèäó ïðåèìóùåñòâåííî ïîäòâåðæäåíèå âûâîäîâ, ñäåëàííûõ ðàíåå î çàêîíîìåðíîñòÿõ ðàçâèòèÿ ìàòåìàòèêè êàê òåîðèè.

I. Способы обоснования математики в
древней Греции от Пифагора до Евклида.

1. Математика пифагорейцев

Ìàòåìàòèêà êàê òåîðèÿ ïîëó÷èëà ðàçâèòèå â øêîëå Ïèôàãîðà (571–479 ãã. äî í. ý.).

Ãëàâíîé çàñëóãîé ïèôàãîðåéöåâ â îáëàñòè íàóêè ÿâëÿåòñÿ ñóùåñòâåííîå ðàçâèòèå ìàòåìàòèêè êàê ïî ñîäåðæàíèþ, òàê è ïî ôîðìå. Ïî ñîäåðæàíèþ — îòêðûòèå íîâûõ ìàòåìàòè÷åñêèõ ôàêòîâ. Ïî ôîðìå — ïîñòðîåíèå ãåîìåòðèè è àðèôìåòèêè êàê òåîðåòè÷åñêèõ, äîêàçàòåëüíûõ íàóê, èçó÷àþùèõ ñâîéñòâà îòâëå÷åííûõ ïîíÿòèé î ÷èñëàõ è ãåîìåòðè÷åñêèõ ôîðìàõ.

Äåäóêòèâíîå ïîñòðîåíèå ãåîìåòðèè ÿâèëîñü ìîùíûì ñòèìóëîì å¸ äàëüíåéøåãî ðîñòà.

Ïèôàãîðåéöû ðàçâèëè è îáîñíîâàëè ïëàíèìåòðèþ ïðÿìîëè­íåéíûõ ôèãóð: ó÷åíèå î ïàðàëëåëüíûõ ëèíèÿõ, òðåóãîëüíèêàõ, ÷åòûðåõóãîëüíèêàõ, ïðàâèëüíûõ ìíîãîóãîëüíèêàõ. Ïîëó÷èëà ðàçâèòèå ýëåìåíòàðíàÿ òåîðèÿ îêðóæíîñòè è êðóãà. Íàëè÷èå ó ïèôàãîðåéöåâ ó÷åíèÿ î ïàðàëåëüíûõ ëèíèÿõ ãîâîðèò î òîì, ÷òî îíè âëàäåëè ìåòîäîì äîêàçàòåëüñòâà îò ïðîòèâíîãî è âïåðâûå äîêàçàëè òåîðåìó î ñóììå óãëîâ òðåóãîëüíèêà. Âåðøèíîé äîñòèæåíèé ïèôàãîðåéöåâ â ïëàíèìåòðèè ÿâëÿåòñÿ äîêàçàòåëüñòâî òåîðåìû Ïèôàãîðà. Ïîñëåäíÿÿ çà ìíîãî ñòîëåòèé ðàíüøå áûëà ñôîðìóëèðîâàíà âàâèëîíñêèìè, êèòàéñêèìè è èíäèéñêèìè ó÷åíûìè, îäíàêî å¸ äîêàçàòåëüñòâî èì íå áûëî èçâåñòíî.

Óñïåõè ïèôàãîðåéöåâ â ñòåðåîìåòðèè áûëè çíà÷èòåëüíûìè. Îíè çàíèìàëèñü èçó÷åíèåì ñâîéñòâ øàðà, îòêðûëè ïîñòðîåíèå ÷åòûðåõ ïðàâèëüíûõ ìíîãîóãîëüíèêîâ — òåòðàýäðà, êóáà, îêòàýäðà è äîäåêàýäðà (èêîñàýäð èññëåäîâàë âïîñëåäñòâèè Ãåýòåò).

Îäíàêî îíè íå ñìîãëè îáîñíîâàòü óòâåðæäåíèÿ, îòíîñÿùèåñÿ ê îáúåìàì òåë (ïèðàìèäû, êîíóñà, öèëèíäðà è øàðà), õîòÿ, êîíå÷íî, ýòè óòâåðæäåíèÿ áûëè óñòàíîâëåíû ýìïèðè÷åñêè ìíîãî âåêîâ ðàíüøå. Íå çíàëè ïèôàãîðåéöû è îòíîøåíèÿ ïîâåðõíîñòè øàðà ê áîëüøîìó êðóãó.  îáëàñòè àðèôìåòèêè ïèôàãîðåéöû èçó÷àëè ñâîéñòâà ÷åòíûõ è íå÷åòíûõ, ïðîñòûõ è ñîñòàâíûõ íàòóðàëüíûõ ÷èñåë, èñêàëè ñîâåðøåííûå ÷èñëà, ò. å. òàêèå, êîòîðûå ðàâíû ñóììå âñåõ ñâîèõ äåëèòåëåé (íàïðèìåð, 6=1+2+3; 28=1+2+4+7+14). Ïî âèäèìîìó, îíè óñòàíîâèëè, ÷òî åñëè ÷èñëî 2^ï –1 ÿâëÿåòñÿ ïðîñòûì, òî ÷èñëî 2^ï–1 ´(2^ï –1) — ñîâåðøåííîå. Ïèôàãîðåéöû çíàëè òàêæå äðîáíûå ÷èñëà è â ýòîé ñâÿçè ðàçðàáîòàëè òåîðèþ àðèôìåòè÷åñêîé è ãåîìåòðè÷åñêîé ïðîïîðöèé. Îíè âëàäåëè ïîíÿòèÿìè ñðåäíåãî àðèôìåòè÷åñêîãî, ñðåäíåãî ãåîìåòðè÷åñ­êîãî è ñðåäíåãî ãàðìîíè÷åñêîãî.

Êàê íè âåëèêè çàñëóãè ïèôàãîðåéöåâ â ðàçâèòèè ñîäåðæàíèÿ è ñèñòåìàòèçàöèè ãåîìåòðèè è àðèôìåòèêè, îäíàêî âñå îíè íå ìîãóò ñðàâíèòüñÿ ñî ñäåëàííûì èìè æå îòêðûòèåì íåñîèçìåðèìûõ âåëè÷èí. Ýòî îòêðûòèå ÿâèëîñü ïîâîðîòíûì ïóíêòîì â èñòîðèè àíòè÷íîé ìàòåìàòèêè.

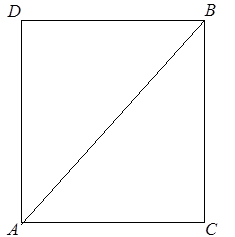
Ïî ïîâîäó ýòîãî îòêðûòèÿ Àðèñòîòåëü ãîâîðèë, ÷òî Ïèôàãîð ïîêàçàë, ÷òî åñëè áû äèàãîíàëü êâàäðàòà áûëà áû ñîèçìåðèìà ñ åãî ñòîðîíîé, òî ÷åòíîå ðàâíÿëîñü áû íå÷åòíîìó.

Ðèñ. 1

Ýòî çàìå÷àíèå Àðèñòîòåëÿ ÿñíî ïîêàçûâàåò, ÷òî ïðè äîêàçàòåëüñòâå íåñîèçìåðèìîñòè äèàãîíàëè êâàäðàòà ñ åãî ñòîðîíîé Ïèôàãîð èñïîëüçîâàë ìåòîä îò ïðîòèâíîãî (ðèñ. 1).

Ïóñòü, äåéñòâèòåëüíî, äèàãîíàëü ÀÂ ñîèçìåðèìà ñî ñòîðîíîé ÀÑ êâàäðàòà ÀÑÂÄ .

Òîãäà 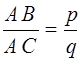, ãäå ð è q — íàòóðàëüíûå ÷èñëà. Äðîáü ìîæíî ñ÷èòàòü íåñîêðàòèìîé (èíà÷å å¸ ìîæíî áûëî áû ñîêðàòèòü); çíà÷èò, ð èëè q áóäåò ÷èñëîì íå÷åòíûì.

Ïðèìåì ÀÑ =1. Ïî òåîðåìå Ïèôàãîðà äîëæíî áûòü:

;

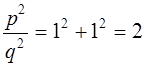Çíà÷èò

,

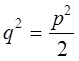ò. å. ð ² äåëèòñÿ íàöåëî íà 2; ñëåäîâàòåëüíî è ð òàêæå äåëèòñÿ íàöåëî íà 2:

ð=2ð ₁ ,

ãäå ð ₁ — íåêîòîðîå íàòóðàëüíîå ÷èñëî.

Àíàëîãè÷íî ïîëó÷àåì:

q=2q ₁ ,

ãäå q ₁ òàêæå íåêîòîðîå íàòóðàëüíîå ÷èñëî.

Èòàê, ð è q — îáà ÷åòíûå ÷èñëà. Ïîñêîëüêó ð èëè q — ÷èñëî íå÷åòíîå, âûõîäèò, ÷òî ÷åòíîå ÷èñëî ðàâíî íå÷åòíîìó ÷èñëó.  êîíöå V âåêà äî í. ý. Ôåîäîð èç Êèðåíû óñòàíîâèë, ÷òî íåñîèçìåðèìîñòü äèàãîíàëè êâàäðàòà ñ åãî ñòîðîíîé íå ÿâëÿåòñÿ èñêëþ÷åíèåì. Îí ïîêàçàë, ÷òî ñòîðîíû êâàäðàòîâ, ïëîùàäè êîòîðûõ ðàâíû 3, 5, 6, …, 17 íåñîèçìåðèìû ñî ñòîðîíîé åäèíè÷íîãî êâàäðàòà. Ïèôàãîð ó÷èë, ÷òî ñóùíîñòü âñåõ âåùåé åñòü ÷èñëî; ÷èñëî — ñàìè âåùè; ãàðìîíèÿ ÷èñåë — ãàðìîíèÿ ñàìèõ âåùåé. Àðèñòîòåëü ãîâîðèë, ÷òî ó ïèôàãîðåéöåâ ÷èñëà ïðèíèìàëèñü çà íà÷àëî è â êà÷åñòâå ìàòåðèè è â êà÷åñòâå [âûðàæåíèÿ äëÿ] èõ ñîñòîÿíèÿ è ñâîéñòâ.

Îòêðûòèå íåñîèçìåðèìûõ âåëè÷èí ñíà÷àëà “âûçâàëî óäèâëåíèå” (Àðèñòîòåëü). Ýòî åñòåñòâåííî: äî îòêðûòèÿ Ïèôàãîðà äðåâíåãðå÷åñêèå ìàòåìàòèêè ñ÷èòàëè, ÷òî ëþáûå äâà îòðåçêà èìåþò îáùóþ ìåðó, õîòÿ, ìîæåò áûòü, è î÷åíü ìàëóþ. Êîãäà, îäíàêî, ïèôàãîðåéöû óáåäèëèñü, ÷òî äîêàçàòåëüñòâî ñóùåñòâî­âàíèÿ íåñîèçìåðèìûõ âåëè÷èí áåçóïðå÷íî, îíè ïîíÿëè, ÷òî èõ ôèëîñîôèÿ îêàçàëàñü â çàòðóäíèòåëüíîì ïîëîæåíèè.

Ïèôàãîðåéöû çíàëè òîëüêî ïîëîæèòåëüíûå öåëûå è äðîáíûå ÷èñëà. Ñëåäóÿ ñâîåé ôèëîñîôñêîé óñòàíîâêå, îíè, ïî ñóòè äåëà, ñ÷èòàëè, ÷òî êàæäàÿ âåùü ìîæåò áûòü îõàðàêòåðèçîâàíà ïîëîæèòåëüíûì öåëûì èëè äðîáíûì ÷èñëîì, êîòîðîå “âûðàæàåò ñóùíîñòü” ýòîé âåùè. Íà äåëå ýòî îçíà÷àëî, ÷òî ãåîìåòðèÿ ñòðîèëàñü íà áàçå àðèôìåòèêè. Îòêðûòèå íåñîèçìåðèìûõ îòðåçêîâ çíàìåíîâàëî ïîýòîìó íà÷àëî êðèçèñà ïèôàãîðåéñêîé ôèëîñîôèè è ìåòîäîëîãè÷åñêèõ îñíîâ ðàçâèâàåìîé èìè ñèñòåìû ìàòåìàòèêè. Ïîñëå îáíàðóæåíèÿ ñóùåñòâîâàíèÿ íåñîèçìåðèìûõ âåëè÷èí ïåðåä ïèôàãîðåéöàìè îòêðûëèñü äâå âîçìîæíîñòè. Ìîæíî áûëî ïîïûòàòüñÿ ðàñøèðèòü ïîíÿòèå ÷èñëà çà ñ÷åò ïðèñîåäèíåíèÿ ê ðàöèîíàëüíûì ÷èñëàì ÷èñåë èððàöèîíàëüíûõ, îõàðàêòåðèçîâàòü íåñîèçìåðèìûå âåëè÷èíû ÷èñëàìè èíîé ïðèðîäû è òàêèì îáðàçîì âîññòàíîâèòü ñèëó ôèëîñîôñêîãî ïðèíöèïà “âñå åñòü ÷èñëî”.

Îäíàêî, ýòîò ïóòü ñòîëü åñòåñòâåííûé è ïðîñòîé ñ ñîâðåìåííîé òî÷êè çðåíèÿ, äëÿ ïèôàãîðåéöåâ áûë çàêðûò.  ýòîì ñëó÷àå íàäî áûëî ïîñòðîèòü äîñòàòî÷íî ñòðîãóþ àðèôìåòè÷åñêóþ òåîðèþ äåéñòâèòåëüíûõ ÷èñåë, ÷òî ïðè óðîâíå ïèôàãîðåéñêîé ìàòåìàòèêè áûëî äåëîì íåâûïîëíèìûì. Ïîýòîìó íàäî áûëî èäòè ïî äðóãîìó ïóòè — ïî ïóòè îïðåäåëåííîãî ïåðåñìîòðà èñõîäíûõ ïðèíöèïîâ, íàïðèìåð ïðèíÿòü, ÷òî ãåîìåòðè÷åñêèå îáúåêòû ÿâëÿþòñÿ âåëè÷èíàìè áîëåå îáùåé ïðèðîäû, ÷åì äðîáíûå è öåëûå ÷èñëà, è ïûòàòüñÿ ñòðîèòü âñþ ìàòåìàòèêó íå íà àðèôìåòè÷åñêîé, à íà ãåîìåòðè÷åñêîé îñíîâå. Èìåííî ýòîò âòîðîé ïóòü è èçáðàëè ïèôàãîðåéöû, à âñëåä çà íèìè áîëüøèíñòâî äðåâíåãðå÷åñêèõ ìàòåìàòèêîâ, âïëîòü äî Àðõèìåäà è Àïîëëîíèÿ.

2. Проблема бесконечности в
древнегреческой философии и математике

 äðåâíåãðå÷åñêîé ôèëîñîôèè ïîíÿòèå áåñêîíå÷íîñòè ïîÿâèëîñü âïåðâûå ó ìàòåðèàëèñòîâ ìèëåòñêîé øêîëû. Àíàêñèìàíäð (610–546 ãã. äî í. ý.), ïåðååìíèê Ôàëåñà, ó÷èë: ìàòåðèÿ áåñêîíå÷íà â ïðîñòðàíñòâå è âî âðåìåíè; âñåëåííàÿ áåñêîíå÷íà, ÷èñëî ìèðîâ áåñê

Учебная работа № 1842. Три кризиса в развитии математики