Учебная работа № 1703. Уравнения математической физики
§ 1.Тема. Некоторые определения и обозначения.
Определение.
Дифференциальным уравнением называется уравнение, содержащее производные неизвестной функции. Если неизвестная функция зависит от одной переменной, то это обыкновенное дифференциальное уравнение, иначе уравнение в частных производных.
Определение.
Наивысший порядок производных неизвестной функции, входящих в уравнение, называется порядком уравнения.
Определение.
Дифференциальное уравнение называется линейным, если производные и сама неизвестная функция входят в уравнение линейным образом.
![]() (1)
(1)
Пусть выбран любой![]() , где
, где ![]() , и его норма:
, и его норма:
 дифференциальный оператор.
дифференциальный оператор.
![]() запись линейного диф. уравнения с помощью диф. оператора. (2)
запись линейного диф. уравнения с помощью диф. оператора. (2)
Определение.
Открытое, связное множество ![]() называется областью.
называется областью.
По умолчанию будем считать область ограниченной.
Через ![]() или
или ![]() будем обозначать границу области.
будем обозначать границу области.
Определение.
![]() (n1)мерное многообразие S в
(n1)мерное многообразие S в ![]() принадлежит классу
принадлежит классу ![]() (
(![]() ), если
), если
для ![]() и
и ![]() такие, что:
такие, что:
![]() , где
, где ![]()
![]() однозначно проектируется на плоскость
однозначно проектируется на плоскость ![]() , при этом:
, при этом:
D проекция данного множества на плоскость ![]()
![]()
![]()
![]()
![]()
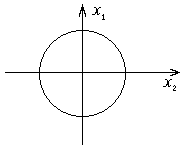

Можно разбить поверхность на части, в каждой части можно одну координату выразить через другие непрерывно дифференцируемой функцией.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Аналогично: ![]()
![]()
§ 2. Классификация линейных уравнений в частных производных второго порядка.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
1.Если ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ex: Уравнение Пуассона
![]()
![]()
2.Если ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ex: ![]()
![]()
Для уравнения Лапласа:
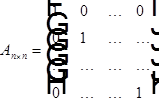
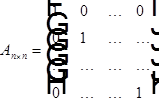
Для волнового уравнения:
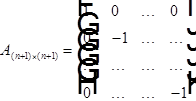
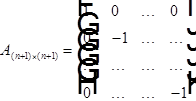
3.Если ![]()
![]()
![]()
![]()
Ex: ![]()
![]()
4.Если ![]()
![]()
Ex: ![]()
![]()
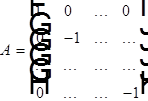
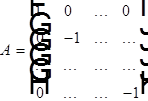
Определение.
Каноническим видом линейного дифференциального уравнения в частных производных называется такой вид, когда матрица A является диагональной.
Приведение к каноническому виду.
1) y=y(x), то:
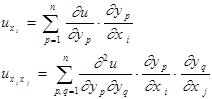
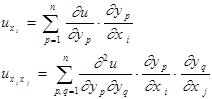
Уравнение (1) в новой системе координат:


Матрица Якоби:


В результате:
|
|
Ex:
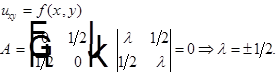
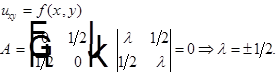
гиперболическое уравнение.
![]()
![]()
Замечание: тип уравнения может быть различный в различных точках.
§ 3.Постановка начальных и краевых задач для уравнений в частных производных.
Задача Коши для волнового уравнения:
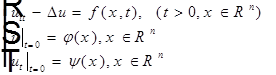
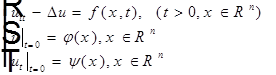
![]()
![]()
Уравнение теплопроводности
![]()
![]()
![]()
![]()
Уравнение Пуассона
![]()
![]()
Определение.
Если малые изменения правой части уравнения приводят к большим изменениям в решении, то задача считается некорректной.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(6)(7.1) первая краевая задача, задача Дирихле.
(6)(7.2) вторая краевая задача, задача Неймана.
(6)(7.3) третья краевая задача.
Волновое уравнение.
![]()
![]()
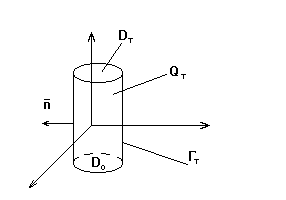

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(8) (9) (10) (11.1) смешанные
(11.2) задачи
(11.3) (краевые задачи)
![]()
![]()
На ![]()
![]()
На боковой поверхности краевые задачи.
Параболическое уравнение.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(12) (13) (14.1) первая, вторая и третья смешанные задачи
(14.2) для уравнения
(14.3) теплопроводности.
(14.1) на границе задана температура;
(14.2) задан тепловой поток;
(14.3) задан теплообмен с окружающей средой.
§ 4. Решение смешанных задач для волнового уравнения методом Фурье (разделением переменных).
Первая смешанная задача.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Собственные значения (5) (6) вещественны, имеют конечную кратность.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
В симметричной матрице собственные вектора, соответствующие разным собственным значениям, попарно ортогональны.
Пусть функции ![]()
![]()
![]()
![]()
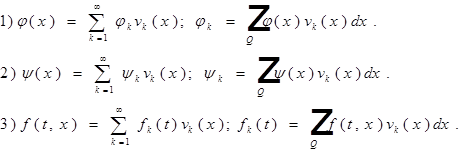
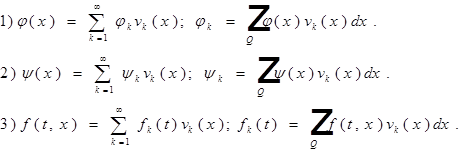
тогда и u(t,x) можно разложить по базису ![]()
![]()
![]()
![]()
Почленно дифференцируем ряд 2 раза:
![]()
![]()
![]()
![]()
Путём разложения решения в ряды по собственным функциям задачи алгебраизуем задачу, получаем счётное число обыкновенных дифференциальных уравнений.




(7) (8) (9) задача.
Решим однородное уравнение для (7):
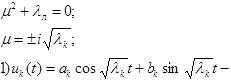
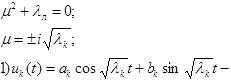
общее решение однородного уравнения (7)
![]()
![]()


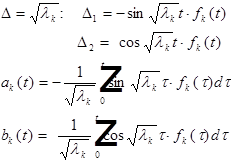
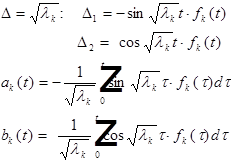
В результате: ![]()
![]()
![]()
![]()
Подставим (8) и (9) в решение:
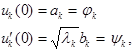
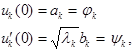
т.е. ![]()
![]()
  |
Замечание: не обоснована сходимость рядов.
§ 5.Решение смешанных задач уравнения теплопроводности методом Фурье (разделения переменных).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
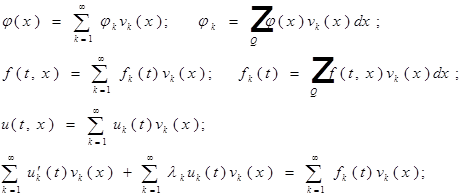
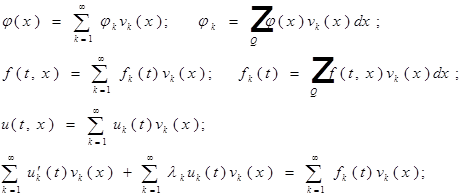
![]()
![]()
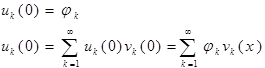
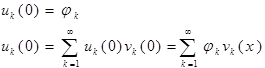
![]()
![]()
![]()
![]()
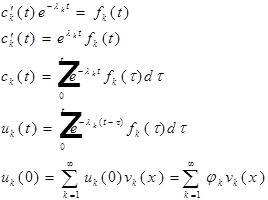
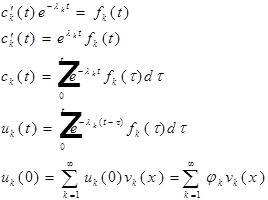
![]()
![]()

 (6 оценок, среднее: 4,67 из 5)
(6 оценок, среднее: 4,67 из 5)