(6 оценок, среднее: 4,67 из 5)
Загрузка...
Учебная работа № 1595. Основная теорема алгебры
Всякий многочлен с любыми комплексными коэффициентами , степень которого не меньше единицы имеет хотя бы один корень, в общем случае комплексный.
План доказательства .
Лемма №1 . Многочлен f(x) является непрерывной функцией комплексного переменного x .
Лемма №2 . Если данн многочлен n ой степени, n>0,
f(x)=a0 xn +a1 xn1 +…+an
с произвольными комплексными коэффициентами и если k любое положительное действительное число, то для достаточно больших по модулю значений
|an xn |>k|axn1 +an xn2 +….+a0 |
Лемма №3 . 
Лемма №4 .(Лемма Даламбера).
Лемма №5.
Если действительная функция комплексного переменного f(x) непрерывна в замкнутом круге Е, то она ограничена.
Лемма №6.
Действительная функция комплексного переменного f(x) непрерывная в замкнутом круге Е достигает своего минимума и максимума.
Доказательство основной теоремы .
Лемма №1.
Надо доказать, что 
|f(x0 +x)f(x0 ) |<e .
Докажем Лемму №1 сначала для многочлена без свободного члена и при x0 =0
Если A=max(|a0 |,|a1 |,…,|a n1 |) и 
(1)
то |f(x)|=|a0 xn +…+an1 x| 
 |
,
 |
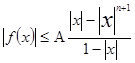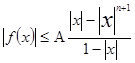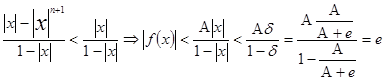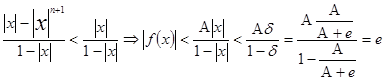т.к |x |<б , и из (1) б <1, то
т.к. a0 =0 то f(0)=0 
Что и требовалось доказать.
Теперь докажем непрерывность любого многочлена.
f(x0 +x)=a0 (x0 +x)n +…+an
pаскрывая все скобки по формуле бинома и собирая вместе члены с
одинаковыми степенями x получим
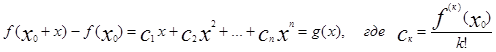
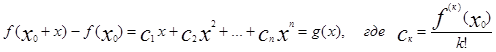
Многочлен g(x)это многочлен от x при x0 =0 и а0 =0 
|f(x0 +x)f(x)|=|g(x)|<e
Лемма доказана.
Лемма №2
Если дан многочлен n ой степени, n>0,
f(x)=a0 xn +a1 xn1 +…+an
с произвольными комплексными коэффициентами и если k любое положительное действительное число, то для достаточно больших по модулю значений x верно неравенство:
|a0 xn |>k|a1 xn1 +a2 xn2 +….+an | (2)
Доказательсво.
Пусть А=max(
), тогда
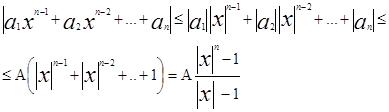
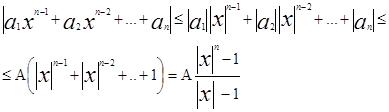
пологая |x| >1, получим
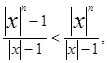
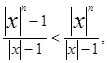
откуда
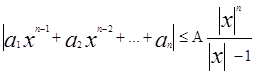
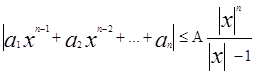
следовательно неравенство (2) будет выполняться если |x|>1 и
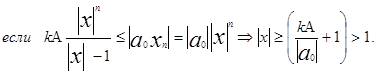
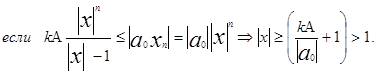
Лемма №2 доказана.
Лемма №3 .
Доказательство.
(3)
применим лемму 2: при k=2 существует такое N1 , что при |x|> N1
|a0 xn |>2|a1 xn1 +a2 xn2 +….+an |
откуда
|a1 xn1 +a2 xn2 +….+an |<|a0 xn |/2
тогда из (3)
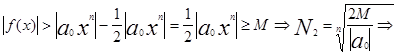
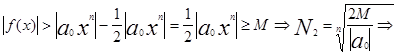
при |x|>N=max(N1 ,N2 ) |f(x)|>M что и тебовалось доказать.
Лемма №3(Лемма Даламбера).
Если при x=x0 многочлен f(x) степени n ,
не обращаеться в нуль, то существует такое приращение h, в общем случае комплексное, что
|f(x0 +h)|<|f(x)|
Доказательство.
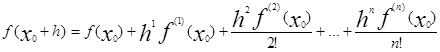
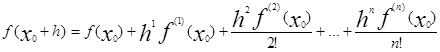
По условию f(x0 ) не равно нулю, случайно может быть так, что x0 является корнем f’(x),..,f(k1) (x). Пусть kя производная будет первой, не имеющей x0 своим корнем. Такое k существует т.к.
f(n) ( x0 )=n!a0
Таким образом
 |
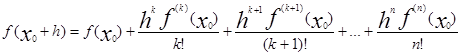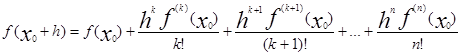Т.к f(x0 ) не равно нулю то поделим обе части уравнения на f(x0 )
и обозначим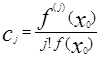 
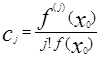
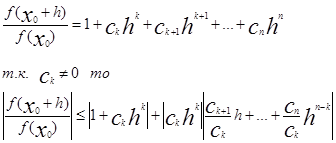
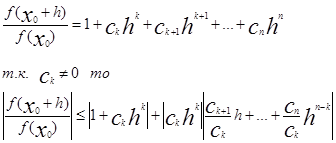
Теперь будем выбирать h. Причем будем отдельно выбирать его модуль и его аргумент.
По лемме№1: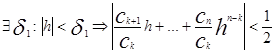 
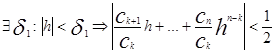
С другой стороны при
(4)
Пусть |h|<min(б1 , б2 ), тогда
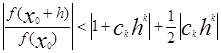
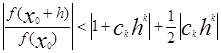
Теперь выберем аргумент h так, чтобы ck hk было действительным отрицательным числом.
При таком выборе ck hk =| ck hk | следовательно учитывая (4) получим
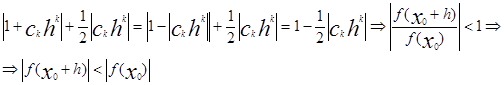
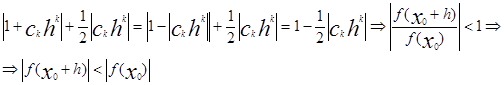
Что доказывает лемму Даламбера.
Лемма №5.
Если действительная функция комплексного переменного f(x) непрерывна в замкнутом круге Е, то она ограничена.
Доказательство.
Предположим, что это не верно тогда
получена бесконечная ограниченная последовательность xn ,
из нее можно выбрать сходящуюся подпоследовательность 
, пусть ее предел равенx0 . Так как круг Е замкнут, то x0 пренадлежит Е. Тогда так как f(x) непрерывна
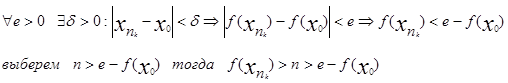
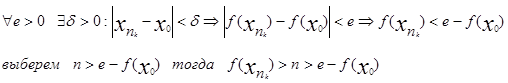
получено противоречие, следовательно неверно, предположение о неограничености f(x) .
Лемма №6.
Действительная функция комплексного переменногоf(x) непрерывная в замкнутом круге Е достигает своего минимума и
максимума.
Доказательство.
Докажем это утверждение для максимума.
Так как f(x) непрерывна в Е, то она ограничена и следовательно существует M =sup{ f(x)} . Рассмотрим функцию 
.
Если f(x) не достигает своего максимума, то M> f(x) следовательно M f(x)>0 , следовательно g(x) непрерывна в Е.
Полученое противоречит тому, что M =sup{ f(x)} . Следовательно функция достигает свего максимума. Аналогично доказывается достижение минимума.
Доказательство основной теоремы.
Пусть дан многочлен f(x), очевидно что если an свободный член, то f(0)= an . Теперь применим лемму№3: возьмем М=|f(0)| =|an | тогда существует такое N, что при |x|>N |f(x)|>M. Теперь возьмем круг Е ограниченный окружностью с центром в нуле и радиусом N, включая границы круга. Так как (по лемме №1) многочлен f(x)непрерывен, то и |f(x)|непрерывен внутри замкнутого круга Е, следовательно(по лемме №6), существует такая точка x0 , что для всех x из E выполняется неравенство |f(x)|>=|f(x0 )|. x0 является точкой минимума для |f(x)| внутри E. Т.к для любого x:|x|>N |f(x)|>M>|f(0)|>|f(x0 )| точка x0 является точкой минимуа |f(x)| на всей комплексной плоскости.
|f(x0 )|=0 т.к по лемме Даламбера если |f(x0 )|¹0 то x0 не точка минимума для |f(x)|Þ x0 корень многочлена f(x).
Теорема доказана.