Учебная работа № 1425. Собственные значения.
1. ВВЕДЕНИЕ
Целый ряд инженерных задач сводится к рассмотрению систем уравнений, имеющих единственное решение лишь в том случае, если известно значение некоторого входящего в них параметра. Этот особый параметр называется характеристическим, или собственным, значением системы. С задачами на собственные значения инженер сталкивается в различных ситуациях. Так, для тензоров напряжений собственные значения определяют главные нормальные напряжения, а собственными векторами задаются направления, связанные с этими значениями. При динамическом анализе механических систем собственные значения соответствуют собственным частотам колебаний, а собственные векторы характеризуют моды этих колебаний. При расчете конструкций собственные значения позволяют определять критические нагрузки, превышение которых приводит к потере устойчивости.
Выбор наиболее эффективного метода определения собственных значений или собственных векторов для данной инженерной задачи зависит от ряда факторов, таких, как тип уравнений, число искомых собственных значений и их характер. Алгоритмы решения задач на собственные значения делятся на две группы. Итерационные методы очень удобны и хорошо приспособлены для определения наименьшего и наибольшего собственных значений. Методы преобразований подобия несколько сложней, зато позволяют определить все собственные значения и собственные векторы.
В данной работе будут рассмотрены наиболее распространенные методы решения задач на собственные значения. Однако сначала приведем некоторые основные сведения из теории матричного и векторного исчислений, на которых базируются методы определения собственных значений.
2. НЕКОТОРЫЕ ОСНОВНЫЕ СВЕДЕНИЯ, НЕОБХОДИМЫЕ ПРИ РЕШЕНИИ ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
В общем виде задача на собственные значения формулируется следующим образом:
AX =lX,
где A — матрица размерности n х n. Требуется найти n скалярных значений l и собственные векторы X, соответствующие каждому из собственных значений.
Основные определения матричного исчисления
1. Матрица A называется симметричной, если
аij = аij, где i, j = 1, 2, . . ., n.
Отсюда следует симметрия относительно диагонали
аkk, где k == 1, 2, . . ., n.
Матрица
| 1 | 4 | 5 |
| 4 | 3 | 7 |
| 5 | 7 | 2 |
является примером симметричной.
2. Матрица A называется трехдиагональной, если все ее элементы, кроме элементов главной и примыкающих к ней диагоналей, равны нулю. В общем случае трехдиагональная матрица имеет вид
| * | * | 0 | |||
| * | * | * | |||
| * | * | * | |||
| . | . | . | . | . | . |
| * | * | * | |||
| 0 | * | * | * | ||
| * | * |
Важность трехдиагональной формы обусловлена тем, что некоторые методы преобразований подобия позволяют привести произвольную матрицу к этому частному виду.
3. Матрица A называется ортогональной, если
АТА = Е,
где Ат—транспонированная матрица A, а Е—единичная матрица. Очевидно, матрица, обратная ортогональной, эквивалентна транспонированной.
4. Матрицы А и В называются подобными, если существует такая несингулярная матрица Р, что справедливо соотношение
В = Р1АР.
Основные свойства собственных значений.
1. Все п собственных значений симметричной матрицы размерности пХп, состоящей из действительных чисел, действительные. Это полезно помнить, так как матрицы, встречающиеся в инженерных расчетах, часто бывают симметричными.
2. Если собственные значения матрицы различны, то ее собственные векторы ортогональны. Совокупность п линейно независимых собственных векторов образует базис рассматриваемого пространства. Следовательно, для совокупности линейно независимых собственных векторов
Xi, где i == 1,. . ., n,
любой произвольный вектор в том же пространстве можно выразить через собственные векторы. Таким образом,
n
Y = S aiXi.
i=1
3. Если две матрицы подобны, то их собственные значения совпадают. Из подобия матриц A и В следует, что
В = Р1АР.
Так как
АХ = lХ,
то
Р1АХ = lР1Х.
Если принять Х == РY, то
Р1АРY = lY,
а
ВY == lY.
Таким образом, матрицы A и В не только имеют одинаковые собственные значения, но и их собственные векторы связаны соотношением
Х = Р Y.
4. Умножив собственный вектор матрицы на скаляр, получим собственный вектор той же матрицы. Обычно все собственные векторы нормируют, разделив каждый элемент собственного вектора либо на его наибольший элемент, либо на сумму квадратов всех других элементов.
3 . ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ.
Пожалуй, наиболее очевидным способом решения задачи на собственные значения является их определение из системы уравнений
(A lE) Х == 0,
которая имеет ненулевое решение лишь в случае, если det(A lE)=0. Раскрыв определитель, получим многочлен пй степени относительно l, корни которого и будут собственными значениями матрицы. Для определения корней можно воспользоваться любым из методов, описанных в гл. 2. К сожалению, в задачах на собственные значения часто встречаются кратные корни. Так как итерационные методы, в этих случаях не гарантируют получение решения, то для определения собственных значений следует пользоваться другими итерационными методами.
Определение наибольшего собственного значения методом итераций
На рис. 1 показана блоксхема простейшего итерационного метода отыскания наибольшего собственного значения системы
AХ = lХ.
Процедура начинается с пробного нормированного вектора X(0). Этот вектор умножается слева на матрицу A, и результат приравнивается произведению постоянной (собственное значение) и нормированному вектору X(0).. Если вектор X(0) совпадает с вектором X(0), то счет прекращается. В противном случае новый нормированный вектор используется в качестве исходного и вся процедура повторяется. Если процесс сходится, то постоянный множитель соответствует истинному наибольшему собственному значению, а нормированный вектор — соответствующему собственному вектору. Быстрота сходимости этого итерационного процесса зависит от того насколько удачно выбран начальный вектор. Если он близок к истинному собственному вектору, то итерации сходятся очень быстро. На быстроту сходимости влияет также и отношение величин двух наибольших собственных значений. Если это отношение близко к единице, то сходимость оказывается медленной.
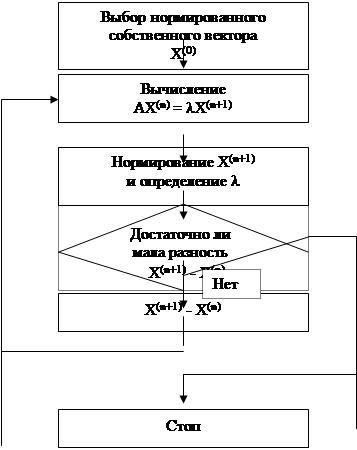 |
Рис. 1. Блоксхема алгоритма иитерационного метода решения задач на собственные значения.
Пример 1
Исследуем трехосное напряженное состояние элемента тела, представленного на рисунке 2. Матрица напряжений для него имеет вид
| 10 | 5 | 6 | |
| 5 | 20 | 4 | * 106 Н/м2 |
| 4 | 30 |
![]()
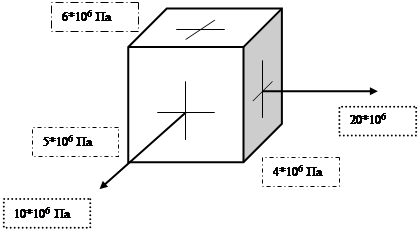 |
Рисунок 2.Трехосное напряженное состояние элемента тела.
Если исходить из того, что разрушение произойдет при максимальном напряжении, то необходимо знать величину наибольшего главного напряжения, которое соответствует наибольшему собственному значению матрицы напряжений. Для нахождения этого напряжения воспользуемся методом итерации Ниже приведена программа для ЭВМ, с помощью которой итерационная процедура осуществляется до тех пор, пока разность между собственными значениями, вычисленными в последовательных итерациях, не станет менее 0,01%. В программе использованы две подпрограммы — GMPRD из пакета программ для научных исследований фирмы IВМ, служащая для перемножения матриц и NORML, нормирующая собственные векторы по наибольшему элементу.
{**********************************************************************}
Программа определения собственных значений Программа позволяет определить наибольшее главное напряжение (собственное значение) для данного трехосного напряженного состояния. Применяется метод итераций. Счет прекращается, когда изменение собственного значения становится менее 0,01 процента или число итераций превышает 50.
{**********************************************************************}
DIMENSION S(3,3),X(3),R(3)
S(1,1) = 10.E06
S(1,2) = 5.ЕО6
S(2,1) = S(1,2)
S(1,3) = 6.E06
S(3,1) = S(1,3)
S(2,2) = 20.E06
S(2,3) = 4.E06
S(3,2) = S(2,3)
S(3,3) =З0.Е06
X(1) = 1.
Х(2) = 0.0
Х(3) = 0.0
XOLD = 0.0
I = 0
WRITE(6 100)
WRITE(6 101)
WRITE(6 102)
WRITE(6 100)
WRITE(6 104) I,X(1),X(2),X(3)
DO 1 1=1,50
CALL GMPRD (S, X, R, 3, 3, 1)
DO 2 J=1,3
2 X(J) = R(J)
CALL NORML(XLAM,X)
WRITE(6,103) I,XLAM,X(1),X(2),X(3)
IF(ABS((XOLDXLAM)/XLAM).LE.0.0001) GO TO 3
XOLD = XLAM
3 WRITE(6,100)
100 FORMAT (1X 54C»’))
FORMAT (2X ‘ITERATION’, ЗХ ‘ITERATION’, 11X,‘EIGENVECTOR’)
FORMAT (3X ‘NUMBER», 6X ,'(N/M**2)’, 5X, ‘X(1)’,
6X,’X(2)’,6X,’X(3)’)
103 FORMAT (1X,I5,7X,E12.5,3F10.5)
104 FORMAT (1X,I5,19X,3F10.5)
STOP
END
{**********************************************************************}
SUBROUTINE NORML(XL,X)
DIMENSION X(3)
{**********************************************************************}
Подпрограмма norml.
Эта подпрограмма находит наибольший из трех элементов собственного вектора и нормирует собственный вектор по этому наибольшему элементу.
{**********************************************************************}
# FIND THE LARGEST ELEMENT
XBIG = X(1)
IF(X(2).GT.XBIG)XBIG=X(2)
IF(X(3).GT.XBIG)XBIG=X(3)
# Нормирование по XBIG
X(l) = X(1)/XBIG
X(2) = X(2)/XBIG
X(3) = X(3)/XBIG
XL = XBIG
RETURN
END
{**********************************************************************}
Результат работы программы получаем в виде:
|
Номер Итерации |
Собственное Значение ( N / M ** 2 ) |
Собственный вектор | ||
| X (1) | X (2) | X (3) | ||
| 0. | 1.00000 | 0. | 0. | |
| 0.10000 Е 08 | 1,00000 | 0.50000 | 0.60000 | |
| 0.26000Е 08 | 0.61923 | 0.66923 | 1.00000 | |
| 0.36392Е 08 | 0.42697 | 0.56278 | 1.00000 | |
| 0.34813Е 08 | 0.37583 | 0.49954 | 1.00000 | |
| 0.34253Е 08 | 0.35781 | 0.46331 | 1.00000 | |
| 0.34000Е 08 | 0.34984 | 0.44280 | 1.00000 | |
| 0.33870Е 08 | 0.34580 | 0.43121 | 1.00000 | |
| 0.33800Е 08 | 0.34362 | 0.42466 | 1.00000 | |
| 0.33760Е 08 | 0,34240 | 0.42094 | 1.00000 | |
| 0.33738Е 08 | 0.34171 | 0.41884 | 1.00000 | |
| 0.33726Е 08 | 0.34132 | 0.41765 | 1.00000 | |
| 0.33719Е 08 | 0,34110 | 0.41697 | 1.00000 | |
| 0.33714Е 08 | 0.34093 | 0.41658 | 1.00000 | |
| 0.33712Е 08 | 0.34091 | 0.41636 | 1.00000 | |
Отметим, что для достижения требуемой точности потребовалось 14 итераций.
Определение наименьшего собственного значения методом итераций
В некоторых случаях целесообразно искать наименьшее, а не наибольшее собственное значение. Это можно сделать, предварительно умножив исходную систему на матрицу, обратную A:
А1АX=lА1X.
Если обе части этого соотношения умножим на 1/l, то получим
1/lХ = A1X.
Ясно, что это уже иная задача на собственное значение, для которой оно равно 1/l, а рассматриваемой матрицей является A1. Максимум 1/l, достигается при наименьшем l. Таким образом, описанная выше итерационная процедура может быть использована для определения наименьшего собственного значения новой системы.
Определение промежуточных собственных значений методом итераций
Найдя наибольшее собственное значение, можно определить следующее за ним по величине, заменив исходную матрицу матрицей, содержащей лишь оставшиеся собственные значения. Используем для этого метод, называемый методом исчерпывания. Для исходной симметричной матрицы A с известным наибольшим собственным значением l1 и собственным вектором X1 можно воспользоваться принципом ортогональности собственных векторов, т. е. записать
ХiT Хj =0 при i<>j и ХiT Хj =1 при i=j.
Если образовать новую матрицу A* в соответствии с формулой
A* =Al1Х1 Х1T,
то ее собственные значения и собственные векторы будут связаны соотношением
А*Xi =liXi.
Из приведенного выше выражения для матрицы A* следует, что
A* Хi = AХi lХ1 Х1TXi.
Здесь при i = 1 свойство ортогональности позволяет привести правую часть к виду
A Х1 l1 Х1.
Но по определению собственных значений матрицы A это выражение должно равняться нулю. Следовательно, собственное значение l1 матрицы A* равно нулю, а все другие ее собственные значения совпадают с собственными значениями матрицы A. Таким образом, матрица A* имеет собственные значения 0, l2, l3,. . ., ln и соответствующие собственные векторы Х1, Х2, Хз,. . . …. Хn. В результате выполненных преобразований наибольшее собственное значение l1 было изъято, и теперь, чтобы найти следующее наибольшее собственное значение l2, можно применить к матрице A* обычный итерационный метод. Определив l2 и Х2, повторим весь процесс, используя новую матрицу A**, полученную с помощью A*, l2 и Х2. Хотя на первый взгляд кажется, что этот процесс должен быстро привести к цели, он имеет существенные недостатки. При выполнении каждого шага погрешности в определении собственных векторов будут сказываться на точности определения следующего собственного вектора и вызывать накопление ошибок. Поэтому описанный метод вряд ли применим для нахождения более чем трех собственных значений, начиная с наибольшего или наименьшего. Если требуется получить большее число собственных значений, следует пользоваться методами преобразования подобия.
4. ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ МЕТОДАМИ ПРЕОБРАЗОВАНИЙ ПОДОБИЯ
Метод преобразований подобия применяется с целью получить из исходной матрицы новую с теми же собственными значениями, но более простого вида. Очевидно, самым лучшим упрощением было бы приведение матрицы к чисто диагональному виду, так как в этом случае собственные значения просто соответствовали бы элементам матрицы, стоящим на главной диагонали. К сожалению, большая часть методов преобразования не позволяет этого сделать, и приходится довольствоваться приведением матрицы к трехдиагональной форме.
Метод Якоби
Метод Якоби позволяет привести матрицу к диагональному виду, последовательно, исключая все элементы, стоящие вне главной диагонали. К сожалению, приведение к строго диагональному виду требует бесконечно большого числа шагов, так как образование нового нулевого элемента на месте одного из элементов матрицы часто ведет к появлению ненулевого элемента там, где ранее был нуль. На практике метод Якоби рассматривают, как итерационную процедуру, которая в принципе позволяет достаточно близко подойти к диагональной форме, чтобы это преобразование можно было считать законченным. В случае симметричной матрицы A действительных чисел преобразование выполняется с помощью ортогональных матриц, полученных в результате вращении в действительной плоскости. Вычисления осуществляются следующим образом. Из исходной матрицы А образуют матрицу A1 == Р1АР1T. При этом ортогональная матрица Р1 выбирается так, чтобы в матрице А1 появился нулевой элемент, стоящий вне главной диагонали. Затем из А1 с помощью второй преобразующей матрицы Р2, образуют новую матрицу A2. При этом Р2, выбирают так, чтобы в A2 появился еще один нулевой внедиагональный элемент. Эту процедуру продолжают, стремясь, чтобы на каждом шаге в нуль обращался наибольший внедиагональный элемент. Преобразующая матрица для осуществления указанной операции на каждом шаге конструируется следующим образом. Если элемент аkl матрицы Ат1 имеет максимальную величину, то Рт соответствует
Pkk = Pll = cos q,
Pkl = Plk = sin q,
Pii = 1 при i <> k, l, Pij = 0 при i <> j.
Матрица Ат будет отличаться от матрицы Am1 только строками и столбцами с номерами k и l. Чтобы элемент аkl(m) был равен нулю, значение q выбирается так, чтобы
2 akl(m1)
tg 2 q = .
akk(m1) – all(m1)
| k | l | |||||||
| 1 | ||||||||
| 1 | ||||||||
| 1 | ||||||||
| 1 | ||||||||
| 1 | ||||||||
| Cos q | . | . | . | . | . | . | sin q | k |
| 1 | ||||||||
| 1 | ||||||||
| Pm = | 1 | |||||||
| 1 | ||||||||
| 1 | ||||||||
| 1 | ||||||||
| sin q | Cos q | l | ||||||
| 1 | ||||||||
| 1 | ||||||||
| 1 | ||||||||
| 1 |
Значения q заключены в интервале
pp
— <= q <= —.
4 4
Пример 2
Пусть требуется найти значения всех главных напряжений для напряженного состояния, показанного на рисунке примера 1. Для этого необходимо найти все собственные значения матрицы напряжений. Такая потребность возникает, если конструктор вместо теории разрушения при максимальном нормальном напряжении намерен пользоваться какойлибо другой теорией разрушения. Чтобы найти все собственные значения, обратимся к методу преобразований Якоби, для реализации которого воспользуемся подпрограммой Е1GЕМ из пакета программ для научных исследований фирмы IВМ, предназначенной для симметричных матриц. Так как матрица симметрична, то она содержит лишь шесть различных элементов. Для экономии памяти подпрограмма ЕIGЕМ использует матрицу 3Х3 в компактной форме, при которой требуется только шесть ячеек памяти. Программа для решения данной задачи имеет вид:
{**********************************************************************}
Программа определение всех главных напряжении трехосной матрицы напряжений.
В программе использовано подпрограмма ЕIGЕМ из пакета программ для научных исследований фирмы IВМ
{**********************************************************************}
DIMENSION S<6),R(?) С
# Задание матрицы в компактной форме
S(1) = 10 Е06
S(2) = 5 Е06
S(3) = 20 Е06
S(4) = 6 Е06
S(5) = 4 Е06
S(6) = 30 Е06
# Определение всех собственных значений методом Якоби
CALL EIGEN(S,R,3,0)
# Печать собственные значении
WRITE(6,100)
WRITE(6,101) S(1),S(3),3(6)
100 FORMAT(1Х,’ТНЕ EIGENVALUES ARE»)
101 FORMAT(1X,E15.8)
STOP
END
Результат работы программы получаем в виде:
Собственные значения равны
0.33709179E 08
0.19149061E 08
0.71417603E 07
Метод Гивенса для симметричных матриц
Метод Гивенса основан на преобразовании подобия, аналогичном применяемому в методе Якоби. Однако в этом случае алгоритм построен таким образом, что вновь образованные нулевые элементы при всех последующих преобразованиях сохраняются. Поэтому метод Гивенса требует выполнения конечного числа преобразований и по сравнению с методом Якоби связан с меньшими затратами машинного времени. Его единственный недостаток состоит в том, что симметричная матрица приводится не к диагональному, а к трехдиагональному виду. Ниже будет показано, что такая форма матрицы может быть весьма полезной и оправдывает усилия, затраченные на ее получение.
В случае матрицы размерности п х п метод Гивенса требует п — 2 основных шагов, на каждом из которых выполняется ряд преобразований, число которых зависит от числа нулей, которое хотят получить в данном столбце или строке. На k м шаге обращают в нули элементы, стоящие вне трех диагоналей kй строки и k го столбца, сохраняя в то же время нулевые элементы, полученные на предыдущих шагах. Таким образом, перед началом k го шага преобразованная матрица является трехдиагональной, если ограничиться рассмотрением ее первых k — 1 строк и столбцов. По мере преобразований симметричная матрица размерности 5х5 приобретает следующие формы:
| * | * | * | * | * | ||
| * | * | * | * | * | ||
| A0= | * | * | * | * | * | исходная матрица, |
| * | * | * | * | * | ||
| * | * | * | * | * |
| * | * | 0 | 0 | 0 | ||
| * | * | * | * | * | ||
| A1= | 0 | * | * | * | * | после первого основного шага, |
| 0 | * | * | * | * | состоящего из трех преобразований, | |
| 0 | * | * | * | * |
| * | * | 0 | 0 | 0 | ||
| * | * | * | 0 | 0 | ||
| A2= | 0 | * | * | * | * | после второго основного шага, |
| 0 | 0 | * | * | * | состоящего из двух преобразований, | |
| 0 | 0 | * | * | * |
| * | * | 0 | 0 | 0 | ||
| * | * | * | 0 | 0 | после третьего основного шага, | |
| A3= | 0 | * | * | * | 0 | состоящего из одного преобразования. |
| 0 | 0 | * | * | * | Теперь матрица имеет трехдиагональный вид. | |
| 0 | 0 | 0 | * | * |
На каждом основном шаге изменяются лишь те элементы матрицы аij, которые расположены в ее правой нижней (заштрихованной) части. Таким образом на kм шаге преобразуется только матрица порядка (п — k + 1), занимающая правый нижний угол исходной матрицы. Ясно, что на каждой следующей стадии выполняется меньшее число преобразований, чем на предыдущей. Всего для приведения матрицы к трехдиагональному виду требуется выполнить (n2 — Зп + 2)/2 преобразований.
Наш опыт применения метода Гивенса показывает, что можно при выполнении одного шага преобразований обратить в нуль сразу все элементы целой строки и столбца, стоящие вне трех диагоналей матрицы. Метод, позволяющий выполнить такое преобразование, предложил Хаусхолдер .
Метод Хаусхолдера для симметричных матриц
Метод Хаусхолдера позволяет привести матрицу к трехдиагональному виду, выполнив почти вдвое меньше вычислений по сравнению с другими методами. Это обусловлено тем, что при его применении становятся нулевыми сразу все элементы строк и столбцов, стоящие вне трех диагоналей матрицы. Метод Хаусхолдера позволяет получить требуемый результат быстрее, чем метод Гивенса, так как связан с выполнением меньшего числа, хотя и более сложных преобразований. Это его свойство особенно ярко проявляется применительно к большим матрицам. Хотя в методе Хаусхолдера вместо плоских вращении используются эрмитовы ортогональные преобразования матриц, трехдиагональная форма матрицы, которую получают этим методом, имеет те же собственные значения, что и трехдиагональная матрица, получаемая методом Гивенса. При использовании метода Хаусхолдера на п — 2 основных шагах выполняются следующие преобразования:
Аk = РkAk1Рk, k=1, 2, …, п2,
где Aо == А.
Каждая преобразующая матрица имеет вид
uk ukT
Pk = E ,
2Kk2
где
ui,k = 0 при i = 1, 2, …, k,
ui,k = ak,i при i = k+2, …, n,
uk+1,k = ak,k+1 ± Sk.
Здесь
![]()
![]() n 1/2
n 1/2
Sk = S a2k,i
i=k+1
2K2k = S2k ± ak, k+1 Sk.
В этих уравнениях берется знак, соответствующий элементу ak,k+1. Это позволяет сделать значение иk+1,k максимальным. Отметим, что методами Гивенса и Хаусхолдера можно пользоваться и в случае несимметричных матриц, приводя их, правда, не к трехдиагональному, а другому частному виду треугольной матрицы известной как матрица Гессенберга:
| * | * | 0 | 0 | 0 | 0 |
| * | * | * | 0 | 0 | 0 |
| * | * | * | * | 0 | 0 |
| * | * | * | * | * | 0 |
| * | * | * | * | * | * |
| * | * | * | * | * | * |
5. ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ СИММЕТРИЧНОЙ ТРЕХДИАГОНАЛЬНОЙ МАТРИЦЫ
Приведя симметричную матрицу к трехдиагональному виду методом Гивенса или Хаусхолдера, необходимо найти ее собственные значения. Чтобы ясней были достоинства трехдиагональной формы, сформулируем задачу о собственных значениях в виде
dеt(А—lE) = 0,
где А — симметричная трехдиагональная матрица. Раcкрыв выражение в скобках, получим
| a1 l | b2 | 0 |
| b1 | a2 l | = 0 |
| bn | ||
| 0 | bn | an l |
Произвольный определитель порядка п можно выразить через п миноров порядка п — 1, каждый из которых в свою очередь выражается через п — 1 миноров порядка п — 2. Удобство трехдиагональной формы в том, что на каждом шаге все миноры, кроме двух, оказываются равными нулю. В результате исходный определитель представляется последовательностью полиномов
fm(l) = (am l) fm1 (l) – b2 m fm2(l).
Приняв
f0 (l) = 1 и f1 (l) = a1 l при r = 2, …. п,
получим совокупность полиномов, известную как последовательность Штурма и обладающую тем свойством, что корни полинома fj (l) располагаются между корнями полинома fj+1 (l). Поэтому для f1 (l) = a1— l можно утверждать, что значение lК = а1 заключено между корнями полинома f2 (l) == (a2 — l) (a1 — l) —b22. Это облегчает итерационное определение корней полинома, так как если известны границы интервалов, в которых лежат значения корней полинома, то их можно найти методом половинного деления. Так последовательно находят корни всех полиномов, и последний из них fn (l) дает все искомые п собственные значения. Эту процедуру можно проиллюстрировать графически (см. рис. 3).
Последовательность Штурма обладает еще и таким свойством: для любого значения b, при котором fn (b) <> 0, число собственных значений матрицы A, больших b, равно числу изменений знака последовательности
1, f1 (b), f2 (b), … , (1)n fn (b).
Если целое число, равное числу изменений знака, обозначить через V(b), то число собственных значений в интервале действительных чисел [b, с] будет равно V(b)—V(c).
|
|
 |
|
|
|
 |
|
|
………………………………………………………………………………………………………..
|
|
 |
|
|
Рис. 3. Итерационное определение корней полинома
6. ДРУГИЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ
В этом разделе мы рассмотрим два метода определения собственных значений, имеющие большое практическое значение. Оба разработаны в последние 20 лет и наиболее эффективны в тех случаях, когда требуется найти все собственные значения произвольной матрицы действительных или комплексных чисел. В обоих используются преобразования, позволяющие получить последовательность подобных матриц, сходящуюся к матрице блочной треугольной формы:
| X1 | * | … | … | * | * | * |
| x2 | * | … | … | * | * | * |
| x3 | … | … | * | * | * | |
| … | … | * | * | * | ||
| … | * | * | * | |||
| … | * | * | ||||
| 0 | … | * | ||||
| * |
где блоки Хm, представляют собой матрицы размерности 2 х 2, расположенные на главной диагонали. Собственные значения блоков Хm, являются в то же время собственными значениями исходной матрицы размерности п x п. Такая форма удобна, так как детерминант второго порядка блоков Хm позволяет определять комплексные собственные значения, не вводя комплексных элементов в окончательную матрицу. Если все собственные значения исходной матрицы действительные, то в окончательном виде она будет треугольной, причем собственные значения будут расположены на диагонали.
Метод LR
Этот метод первоначально был разработан Рутисхаузером в 1958 г. Метод основан на представлении матрицы A в виде произведения
А = LR,
где L — левая треугольная матрица с единичными диагональными элементами, а R — правая треугольная. Применяя преобразование подобия L1 AR, видим, что,
A2 = L1 A R = L1 (RL)L = R L.
Следовательно,
Am1 = Lm1 Rm1,
Am = R m1 Lm1.
Этот процесс повторяется до тех пор, пока Ls не превратится в единичную матрицу Е, а Rs не приобретет квазидиагональную форму. Хотя этот метод очень удобен, он не всегда устойчив. Поэтому предпочтение часто отдают другому методу.
Метод QR
Метод QR. предложен Фрэнсисом в 1961 г. Соответствующий ему алгоритм определяется соотношением
Am = Q m Rm.
где Qm — ортогональная матрица, а Rm — верхняя треугольная матрица. При использовании метода последовательно получаем
Am+1 = Q mT Am Q m = Q mT Q m Rm Q m = Rm Q m.
В пределе последовательность матриц А стремится к квазидиагональной форме. Этот метод сложнее предыдущего и требует больших затрат машинного времени. Однако его устойчивость,обусловленная использованием ортогональных преобразующих матриц, обеспечила ему прочную репутацию лучшего метода решения задач самой общей формы.
Пример 3
Пусть требуется найти все собственные значения произвольной матрицы размерности 6 x 6
| 2,3 | 4,3 | 5,6 | 3,2 | 1,4 | 2,2 |
| 1,4 | 2,4 | 5,7 | 8,4 | 3,4 | 5,2 |
| 2,5 | 6,5 | 4,2 | 7,1 | 4,7 | 9,3 |
| 3,8 | 5,7 | 2,9 | 1,6 | 2,5 | 7,9 |
| 2,4 | 5,4 | 3,7 | 6,2 | 3,9 | 1,8 |
| 1,8 | 1,7 | 3,9 | 4,6 | 5,7 | 5,9 |
Сделаем это в два приема, приведя сначала матрицу с помощью преобразования подобия к виду Гсссенберга, затем с помощью разновидности метода QRнайдем собственные значения. В приведенной ниже программе использованы две подпрограммы из пакета программ для научных исследований фирмы IВМ. Подпрограмма НSВС преобразует матрицу размерности 6 x 6 к форме Гессенберга, а подпрограмма АТЕIG позволяет найти собственные значения.
{**********************************************************************}
Программа определение всех собственных значений произвольной матрицы размерности 6х5. Используются подпрограммы НSВС и АТЕIG из пакета программ для научных исследований фирмы IBM
{**********************************************************************}
DIMENSION A(6,6),RR(6),RI(6),IANA(6)
READ(5,100)((A(I,J),J=1,6),I=1,6)
WRITE(6,104)
104 FORMAT(///lX,’THE ORIGINAL MATRIX IS AS FOLLOWS’)
WRITE(6,103)
103 FORMAT(1X,65(»))
WRITE(6,101)((A(I,J),J=1,6),I=1,6)
WRITE(6,103)
FORMAT(6(1X,F10.5))
100 FORMAT(6F10.5)
CALL HSBG(6,A,6)
WRITE(6,105)
105 FORMAT(///1X,’THE MATRIX W HESSENBUR5 FORM IS’) WRITE(6,103)
WRITE(6,101)((A(I,J),J=1,6),I=1,6)
WRITE(6,103)
CALL ATEIG(6,A,RR,RI,IANA,6)
WRITE(6,106)
FORHAT(///1X,’THE EIGENVALUES ARE AS FOLLOUS’)
WRITE(6,107)
107 FORMAT (1X, 23(‘‘),/,4X,’REAL’,12X,’IMAG’,/,23(‘‘))
WRITE(6,102)(RR(I),PKI),I=1,6)
WRITE(6,108)
108 FORMAT(1X,23(‘‘))
FORMAT<2(2X,F10.5)»
STOP
END
Результат получаем в виде
Исходная матрица имеет вид
| 2.30000 | 4.30000 | 5.60000 | 3.20000 | 1,40000 | 2.20000 |
| 1.40000 | 2.40000 | 5.70000 | 8.40000 | 3.40000 | 5.20000 |
| 2.50000 | 6.50000 | 4.20000 | 7.10000 | 4.70000 | 9.30000 |
| 3.80000 | 5.70000 | 2.90000 | 1.60000 | 2.50000 | 7.90000 |
| 2.40000 | 5.40000 | 3.70000 | 6.20000 | 3.90000 | 1.80000 |
| 1.80000 | 1.70000 | 3.90000 | 4.60000 | 5.70000 | 5.90000 |
Матрица в форме Гессенберга.
| 1.13162 | 3.20402 0, | 0.05631 | 3.88246 | 1.40000 | 2.20000 |
| 0.75823 | 0.07468 0, | 0.48742 | 6.97388 | 5.37А35 | 10.36283 |
| 0. | 1.13783 2, | 2.63803 | 10.18618 | 7.15297 | 17.06242 |
| 0. | 0. | 3.35891 | 7. 50550 | 7.09754 | 13.92154 |
| 0. | 0. | 0. | 13.36279 | 10.58947 | 16.78421 |
| 0. | 0. | 0. | 0. | 5.70000 | 5.90000 |
Собственные значения
Действит. Миним.
| 25.52757 | 0. |
| 5.63130 | 0. |
| 0.88433 | 3.44455 |
| 0.88433 | 3.44455 |
| 0.68247 | 1.56596 |
| 0.68247 | 1.56596 |
7. ВЫБОР АЛГОРИТМА РЕШЕНИЯ ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
Выбор подходящего алгоритма для решения той или иной задачи на собственные значения определяется типом собственных значений, типом матрицы и числом искомых собственных значений. Чем сложнее задача, тем меньше число алгоритмов, из которых можно выбирать. Таблица 1 позволяет облегчить этот выбор. Обычно пакеты математического обеспечения ЭВМ содержат подпрограммы, в которых используются все эти алгоритмы или некоторые из них. Одним из эффективных способов использования имеющегося математического обеспечения является одновременное применение двух подпрограмм, позволяющее совместить их лучшие качества. Например, имея матрицу общего вида, можно методом Хаусхолдера свести ее к виду Гессенберга, а затем с помощью алгоритма QR найти собственные значения. При этом будут использованы как быстрота, обеспечиваемая методом Хаусхолдера, так и универсальность алгоритма QR.
Таблица 1 Выбор алгоритма решения задачи на собственные значения
|
Название алгоритма |
Применяется для |
Результат |
Рекомендуется для отыскания собственных значений |
Примечание |
||
| Наибольшего или наименьшего | Всех <=6 | Всех >=6 | ||||
| Определитель (итерация) | Матриц общего вида | Собственные значения | * | Требует нахождения корней полинома общего вида | ||
|
Итерация (итерация) |
То же |
Собственные значения и собственные векторы |
* |
* |
* |
Обеспечивает наилучшую точность для наибольшего и наименьшего собственных значений |
| Метод Якоби (преобразование) | Симметричных матриц | Диагональная форма матрицы |
* |
* |
Теоретически требует бесконечного числа шагов | |
|
Метод Гивенса (преобразование) |
То же |
Трехдииональльная форма матрицы |
* |
* |
Требует знания корней простого полинома | |
| Несимметричных матриц | Форма Гессенберга |
* |
* |
Требует применения дополнительного метода | ||
| Метод Хаусхолдера (преобразование) | Симметричных матриц | Трехдиагональная форма матрицы |
* |
* |
Требует знания корней простого полинома | |
| Метод Хаусхолдера (преобразование) | Несимметричных матриц | Форма Гессенберга | * | * | Требует применения дополнительного метода | |
| Метод LR (преобразование) | Матриц общего вида | Квазидиагональная форма матрицы |
* |
* |
Бывает неустойчив | |
| Метод QR (преобразование) |
То же |
То же |
* |
* |
Лучший метод, обладающий наибольшей общностью | |

 (6 оценок, среднее: 4,67 из 5)
(6 оценок, среднее: 4,67 из 5)