(6 оценок, среднее: 4,67 из 5)
Загрузка...
Учебная работа № 1420. Математическое ожидание и дисперсия для интервальных и пропорциональных шкал. Доверительные интервалы
.
С.В. Усатиков, кандидат физмат наук, доцент; С.П. Грушевский, кандидат физмат наук, доцент; М.М. Кириченко, кандидат социологических наук
Рассмотрим случай, когда в проводимом эксперименте числовая шкала имеет единицу измерения, т.е. про полученные числовые величины всегда можно сказать, насколько одно больше другого. Например, х это число ошибок, допущенных при какомлибо тестировании, или число правильных ответов. Обозначим х1,…,хк деления этой шкалы, а n1,…,nk частоты или число попаданий случайной величины х на каждое из этих делений. Например, в тестировании: шкала х1=0 правильных ответов, …, хк=к1 правильных ответов; n1 тестируемых не дали ни одного правильного ответа, …, nk тестируемых дали к1 правильных ответов.
Математическим ожиданием или просто средним называется число mx, вычисляемое по следующему правилу:
mx= 
(n1x1+…..+nkxk),
где n=n1+…+nk общее число испытаний
Дисперсией называется число , 
вычисляемое по следующему правилу:
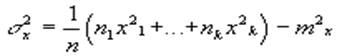чаще используется число 
, которое называется стандартным отклонением.
Например, группу из n=11 учащихся опросили и получили следующее число правильных ответов:
| Шкала Xi | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| Частоты ni | 0 | 1 | 0 | 1 | 1 | 2 | 2 | 2 | 1 | 0 | 1 | 0 |
Здесь 9 правильных ответов дал только один человек, 10 ни одного, 13 правильных ответов дали 2 человека и т.п. Тогда:
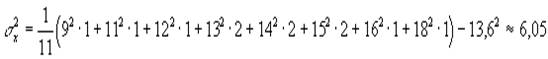или 
Таким образом, mx является обобщенным показателем достигнутого группой уровня в среднем, в виде одного числа, как меры центральной тенденции. Число же s x показывает, насколько испытуемые в группе отличаются по уровню развития изучаемого признака. Чем больше s x, тем больше различия у испытуемых, тем более разнородна по составу группа. Наоборот, чем меньше s x , тем однороднее группа и тем ближе по своему уровню испытуемые.
Дисперсия весьма важный для исследователяпрактика показатель. Анализируя ту или иную сторону учебновоспитательного процесса, необходимо сравнивать большие наборы средних арифметических. Скажем, если опрос проводили в пяти классах параллели, а анкета содержала 15 вопросов с интервальной шкалой, каковой приписывались балльные значения, то общее число значений средних арифметических достигает 75. При этом самый опытный исследователь может запутаться в расчетах и пропустить какуюлибо зависимость (или же обнаружить ее там, где она никогда не существовала). Это делать довольно легко, так как средняя арифметическая, как мера центральной тенденции, обладает рядом весьма капризных свойств. Понять их помогает приводимая ниже таблица.
“Удовлетворяют ли Вас результаты проведенной аттестации ?”
| Позиция вопроса | Да, в полной мере | В общем да, за исключением нескольких моментов | Скорее всего нет | Совершенно не удовлетворяет | Трудно сказать |
| Балльное значение, приписанное позиции | +2 | +1 | 1 | 2 | 0 |
| Выборка 1 | 20% | 20% | 20% | 20% | 20% |
| Выборка 2 | 0% | 50% | 50% | 0% | 0% |
| Выборка 3 | 0% | 0% | 0% | 0% | 100% |
| Выборка 4 | 10% | 10% | 10% | 10% | 60% |
Если мы рассчитаем результаты этих четырех опросов, то получим, что во всех случаях mx=0. Разумеется, вероятность получить столь явно расходящиеся, как в нашей таблице, распределения, равна нулю в практике возможны лишь какиелибо приблеженные варианы. Но наш пример носит чисто иллюстративный характер. Он позволяет понять почему в большинстве случаев исследователь, приводя значения mx по серии групп опрошенных, указывает и на размер дисперсии. В нашем примере при полном равенстве mх значения дисперсии будут разлисчаться очень сильно от минимума в выборке 3 (дисперсия отсутствует вообще) до максимума в выборке 1.
Справедливости ради надо отметить, что неудобства причиняемые исследователю средним арифметическим, как мерой центральной тенденции, носят не только математический, но также и логический характер. Последнее обстоятельство не совсем относится к сути данной проблемы, но мы считаем необходимым о нем упомянуть, так как с ошибками такого рода сталкиваться приходится довольно часто. Проблема связана с тем, что ни в одной анкете не возможно дать вопросы, хотя бы приблизительно равные по степени сложности. На вопрос “Укажите Ваш разряд: 10,11,12,…15 (обведите кружком)” ответят практически все и ответы на 100% будут совпадать с действительностью. Вопрос о взаимоотношениях с администрацией вызовет большие сложности в заполнее и большее число уклонений от ответа. А оценить, например, преимущества методик школы Монтессори смогут весьма не многие, (да и с теми, кто такую оценку произвел, надо еще разобраться, используя “вопросыфильтры” и “вопросыловушки” не затесались ли туда те, чья информированность о Монтессори ограничивается газетной заметкой). Поэтому всегда возникает вопрос включать ли в знаменатель формулы среднего арифметического тех, кто избрал вариант “Затрудняюсь ответить, не знаю” или нет ?
Расхождения могут быть весьма значительными. Например, если группа учителей оценивает какуюлибо сторону педагогического процесса следующим образом:
| “отличную” | “хорошую” |