Учебная работа № 1338. Теория игр и принятие решений
В зависимости от условий внешней среды и степени информативности лица принимающего решение (ЛПР) производится следующая классификация задач принятия решений:
а) в условиях риска;
б) в условиях неопределённости;
в) в условиях конфликта или противодействия (активного противника).
Теория полезности и принятия решений.
Принятие решений в условиях риска.
Критерий ожидаемого значения.
Использование критерия ожидаемого значения обусловлено стремлением максимизировать ожидаемую прибыль (или минимизировать ожидаемые затраты). Использование ожидаемых величин предполагает возможность многократного решения одной и той же задачи, пока не будут получены достаточно точные расчётные формулы. Математически это выглядит так: пусть Х– случайная величина с математическим ожиданием MX и дисперсией DX. Если x1 ,x2 ,…,xn – значения случайной величины (с.в.) X, то среднее арифметическое их (выборочное среднее) значений ![]() имеет дисперсию
имеет дисперсию ![]() . Таким образом, когда n®¥
. Таким образом, когда n®¥
![]() ® 0 и
® 0 и ![]() ®MX.
®MX.
Другими словами при достаточно большом объёме выборки разница между средним арифметическим и математическим ожиданием стремится к нулю (так называемая предельная теорема теории вероятности). Следовательно, использование критерия ожидаемое значение справедливо только в случае, когда одно и тоже решение приходится применять достаточно большое число раз. Верно и обратное: ориентация на ожидания будет приводить к неверным результатам, для решений, которые приходится принимать небольшое число раз.
Пример 1. Требуется принять решение о том, когда необходимо проводить профилактический ремонт ПЭВМ, чтобы минимизировать потери изза неисправности. В случае если ремонт будет производится слишком часто, затраты на обслуживание будут большими при малых потерях изза случайных поломок.
Так как невозможно предсказать заранее, когда возникнет неисправность, необходимо найти вероятность того, что ПЭВМ выйдет из строя в период времени t. В этом и состоит элемент ”риска”.
Математически это выглядит так: ПЭВМ ремонтируется индивидуально, если она остановилась изза поломки. Через T интервалов времени выполняется профилактический ремонт всех n ПЭВМ. Необходимо определить оптимальное значение Т, при котором минимизируются общие затраты на ремонт неисправных ПЭВМ и проведение профилактического ремонта в расчёте на один интервал времени.
Пусть рt – вероятность выхода из строя одной ПЭВМ в момент t, а nt – случайная величина, равная числу всех вышедших из строя ПЭВМ в тот же момент. Пусть далее С1 – затраты на ремонт неисправной ПЭВМ и С2 – затраты на профилактический ремонт одной машины.
Применение критерия ожидаемого значения в данном случае оправдано, если ПЭВМ работают в течение большого периода времени. При этом ожидаемые затраты на один интервал составят
ОЗ = 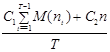 ,
,
где M(nt ) – математическое ожидание числа вышедших из строя ПЭВМ в момент t. Так как nt имеет биномиальное распределение с параметрами (n, pt ), то M(nt ) = npt . Таким образом
ОЗ = 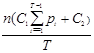
Необходимые условия оптимальности T* имеют вид:
ОЗ (T* 1) ³ ОЗ (T* ),
ОЗ (T* +1) ³ ОЗ (T* ).
Следовательно, начиная с малого значения T, вычисляют ОЗ(T), пока не будут удовлетворены необходимые условия оптимальности.
Пусть С1 = 100; С2 = 10; n = 50. Значения pt имеют вид:
| T | рt | ОЗ(Т) | |
| 1 | 0.05 | 0 | |
| 2 | 0.07 | 0.05 | 375 |
| 3 | 0.10 | 0.12 | 366.7 |
| 4 | 0.13 | 0.22 | 400 |
| 5 | 0.18 | 0.35 | 450 |
T* ® 3 , ОЗ(Т* ) ® 366.7
Следовательно профилактический ремонт необходимо делать через T* =3 интервала времени.
Критерий “ожидаемое значение – дисперсия”
Критерий ожидаемого значения можно модифицировать так, что его можно будет применить и для редко повторяющихся ситуаций .
Если х – с. в. с дисперсией DX, то среднее арифметическое ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Пример 2. Применим критерий “ожидаемое значение – дисперсия” для примера 1. Для этого необходимо найти дисперсию затрат за один интервал времени, т.е. дисперсию
зТ =

Т.к. nt , t =![]()
![]()
D(зТ ) = D(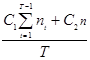
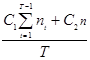
![]()
![]()
![]()
![]()
![]()
![]()
![]()
= ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
где С2 n = const.
Из примера 1 следует, что
М(зТ ) = М(з(Т)).
Следовательно искомым критерием будет минимум выражения
М(з(Т)) + к D(зТ ).
Замечание. Константу “к” можно рассматривать как уровень не склонности к риску, т.к. “к” определяет “степень возможности” дисперсии Д(зТ ) по отношению к математическому ожиданию. Например, если предприниматель, особенно остро реагирует на большие отрицательные отклонения прибыли вниз от М(з(Т)), то он может выбрать “к” много больше 1. Это придаёт больший вес дисперсии и приводит к решению, уменьшающему вероятность больших потерь прибыли.
При к =1 получаем задачу
![]()
![]()
![]()
![]()
По данным из примера 1 можно составить следующую таблицу
| Т | pt | pt 2 | М(з(Т))+D(з(Т)) | ||
| 1 | 0.05 | 0.0025 | 0 | 0 | 500.00 |
| 2 | 0.07 | 0.0049 | 0.05 | 0.0025 | 6312.50 |
| 3 | 0.10 | 0.0100 | 0.12 | 0.0074 | 6622.22 |
| 4 | 0.13 | 0.0169 | 0.22 | 0.0174 | 6731.25 |
| 5 | 0.18 | 0.0324 | 0.35 | 0.0343 | 6764.00 |
Из таблицы видно, что профилактический ремонт необходимо делать в течение каждого интервала Т* =1.
Критерий предельного уровня.
Критерий предельного уровня не дает оптимального решения, максимизирующего, например, прибыль или минимизирующего затраты. Скорее он соответствует определению приемлемого способа действий.
Пример 3. Предположим, что величина спроса x в единицу времени (интенсивность спроса) на некоторый товар задаётся непрерывной функцией распределения f(x). Если запасы в начальный момент невелики, в дальнейшем возможен дефицит товара. В противном случае к концу рассматриваемого периода запасы нереализованного товара могут оказаться очень большими. В обоих случаях возможны потери.
Т.к. определить потери от дефицита очень трудно, ЛПР может установить необходимый уровень запасов таким образом, чтобы величина ожидаемого дефицита не превышала А1 единиц, а величина ожидаемых излишков не превышала А2 единиц. Иными словами, пусть I– искомый уровень запасов. Тогда
ожидаемый дефицит = ![]()
![]()
ожидаемые излишки =![]()
![]()
При произвольном выборе А1 и А2 указанные условия могут оказаться противоречивыми. В этом случае необходимо ослабить одно из ограничений, чтобы обеспечить допустимость.
Пусть, например,
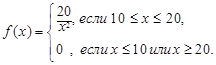
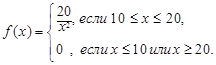
![]()
![]()
Тогда
![]()
![]()

 (5 оценок, среднее: 4,60 из 5)
(5 оценок, среднее: 4,60 из 5)