Учебная работа № 1208. Матричные операции в вейвлетном базисе

Учебная работа № 1208. Матричные операции в вейвлетном базисе

Курсовая работа студентки 3 курса Громовой Марии Михайловны

Белорусский государственный университет

Факультет прикладной математики и информатики

Кафедра математической физики

Минск 2003

Вейвлетпреобразование сигналов (wavelet transform), теория которого оформилась в начале 90х годов, является не менее общим по областям своих применений, чем классическое преобразование Фурье. Принцип ортогонального разложения по компактным волнам состоит в возможности независимого анализа функции на разных масштабах ее изменения. Вейвлетпредставление сигналов (функций времени) является промежуточным между полностью спектральным и полностью временным представлениями.

Компактные волны относительно независимо были предложены в квантовой физике, физике электромагнитных явлений, математике, электронике и сейсмогеологии. Междисциплинарные исследования привели к новым приложениям данных методов, в частности, в сжатии образов для архивов и телекоммуникаций, в исследованиях турбулентности, в физиологии зрительной системы, в анализе радарных сигналов и предсказании землетрясений. К сожалению, объем русскоязычной научной литературы по тематике вейвлетпреобразований (да и нейронных сетей) относительно невелик.

Базовая идея восходит к временам 200летней давности и принадлежит Фурье: аппроксимировать сложную функцию взвешенной суммой простых функций, каждая из которых, в свою очередь, получается из одной функциипрототипа. Эта функцияпрототип выполняет роль строительного блока, а искомая аппроксимация получается комбинированием одинаковых по структуре блоков. При этом, если «хорошая» аппроксимация получается при использовании небольшого числа блоков, то тем самым достигается значительное уплотнение информации. В качестве таких блоков Фурье использовал синусоиды с различными периодами.

Что прежде всего отличает вейвлетанализ от анализа Фурье? Основным недостатком Фурьепреобразования является его «глобальная» чувствительность к «локальным» скачкам и пикам функции. При этом модификация коэффициентов Фурье (например, обрезание высоких гармоник с целью фильтрации шума) вносит одинаковые изменения в поведение сигнала на всей области определения. Это особенность оказывается полезной для стационарных сигналов, свойства которых в целом мало меняются со временем.

При исследовании же нестационарных сигналов требуется использование некоторых локализованных во времени компактных волн, коэффициенты разложения по которым сохраняют информацию о дрейфе параметров аппроксимируемой функции. Первые попытки построения таких систем функций сводились к сегментированию сигнала на фрагменты («окна») с применением разложения Фурье для этих фрагментов. Соответствующее преобразование оконное преобразование Фурье было предложено в 194647 годах Jean Ville и, независимо, Dennis Gabor. В 195070х годах разными авторами было опубликовано много модификаций временичастотных представлений сигналов.

В конце 70х инженергеофизик Морли (Jean Morlet) столкнулся с проблемой анализа сигналов, которые характеризовались высокочастотной компонентой в течение короткого промежутка времени и низкочастотными колебаниями при рассмотрении больших временных масштабов. Оконные преобразования позволяли проанализировать либо высокие частоты в коротком окне времени, либо низкочастотную компоненту, но не оба колебания одновременно. В результате был предложен подход, в котором для различных диапазонов частот использовались временные окна различной длительности. Оконные функции получались в результате растяжениясжатия и смещения по времени гаусиана. Morlet назвал эти базисные функции вейвлетами (wavelets) компактными волнами. В дальнейшем благодаря работам Мейера (Yves Meyer), Добеши (Ingrid Daubechies), Койфмана (Ronald Coifman), Маллы (Stephane Mallat) и других теория вейвлетов приобрела свое современное состояние.

Среди российских ученых, работавших в области теории вейвлетов, необходимо отметить С.Б. Стечкина, И.Я. Новикова, В.И. Бердышева.

1. Многомасштабный анализ и вейвлеты

Определение 1. Многомасштабный анализ (multiresolutional analysis) – разложение гильбертова пространства L² (R^d ), d³1, в последовательность замкнутых подпространств

, (1.1)

обладающих следующими свойствами:

1. , и полно в L² (R^d ),

2. Для любого fÎ L² (R^d ), для любого jÎ Z, f(x)ÎV_j тогда и только тогда, когда

f(2x) ÎV_j1 ,

3. Для любого fÎ L² (R^d ), для любого kÎ Z^d , f(x)ÎV₀ тогда и только тогда, когда f(xk)ÎV₀ ,

4. Существует масштабирующая (scaling) функция jÎV₀ , что {j(xk)}_kÎZ ^d образует

базис Ритца в V₀ .

Для ортонормальных базисов можно переписать свойство 4 в виде:

4’. Существует масштабирующая функция jÎV₀ , что {j(xk)}_kÎZ ^d образует ортонормальный базис в V₀ .

Определим подпространство W_j как ортогональное дополнение к V_j в V_j1 ,

, (1.2)

и представим пространство L² (R^d ) в виде прямой суммы

(1.3)

Выбирая масштаб n, можем заменить последовательность (1.1) следующей последовательностью:

(1.4)

и получить

(1.5)

Если имеем конечное число масштабов, то, не нарушая общности, можно положить j=0 и рассматривать

, V₀ Î L² (R^d ) (1.6)

вместо (1.4). В числовой реализации подпространство V₀ конечномерно.

Функция j так называемая масштабирующая (скейлинг) функция. С ее помощью можно определить функцию y вейвлет такую, что набор {y(xk)}_kÎZ образует ортонормальный базис в W₀ . Тогда

, m=0..M1. (1.7)

Из свойства 4’ непосредственно следует, что, вопервых, функция j может быть представлена в виде линейной комбинации базисных функций пространства V₁ . Так как функции {j_j,k (x)=2^j/2 j(2^j xk)}_kÎZ образуют ортонормальный базис в V_j , то имеем

. (1.8)

Вообще говоря, сумма в выражении (1.8) не обязана быть конечной. Можно переписать (1.8) в виде

, (1.9)

где

, (1.10)

а 2pпериодическая функция m₀ определяется следующим образом:

. (1.11)

Вовторых, ортогональность {j(xk)}_kÎZ подразумевает, что

(1.12)

и значит

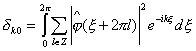(1.13)

и . (1.14)

Используя (1.9), получаем

(1.15)

и, рассматривая сумму в (1.15) по четным и нечетным индексам, имеем

. (1.16)

Используя 2pпериодичность функции m₀ и (1.14), после замены x/2 на x, получаем необходимое условие

(1.17)

для коэффициентов h_k в (1.11). Заметив, что

(1.18)

и определив функцию y следующим образом:

, (1.19)

где

, k=0,…,L1 , (1.20)

или преобразование Фурье для y

, (1.21)

где

, (1.22)

можно показать, что при каждом фиксированном масштабе jÎZ вейвлеты

{y_j,k (x)=2^j/2 y(2^j xk)}_kÎZ образуют ортонормальный базис пространства W_j .

Равенство (1.17) определяет пару квадратурных зеркальных фильтров (quadrature mirror filters, QMF) H и G, где и . Коэффициенты QMF H и G вычисляются с помощью решения системы алгебраических уравнений. Число L коэффициентов фильтра в (1.11) и (1.22) связано с числом исчезающих моментов М, и всегда четно.

Выбранный фильтр Н полностью определяет функции j и y и, таким образом, многомасштабный анализ. Кроме того, в правильно построенных алгоритмах значения функций j и y почти никогда не вычисляются. Благодаря рекурсивному определению вейвлетного базиса, все операции проводятся с квадратурными зеркальными фильтрами H и G, даже если в них используются величины, связаные с j и y.

2. Быстрое вейвлетпреобразование

После того, как вычислены коэффициенты h_k и g_k , т.е. выбран определенный вейвлет, можно проводить вейвлетпреобразование сигнала f(x), поскольку задан ортонормальный базис (y_j,k, j _j,k ). Любая функция f(x)ÎL² (R) полностью характеризуется ее вейвлеткоэффициентами разложения по этому базису и потому может быть представлена формулой

. (2.1)

Зададим все пределы суммирования в формуле (2.1). Функцию f(x) можно рассматривать на любом nм уровне разрешения j_n . Тогда разделение между ее усредненными значениями на этом уровне и флуктуациями вокруг них выглядят как

. (2.4)

На бесконечном интервале первая сумма может быть опущена, и в результате получается «чистое» вейвлетразложение.

Коэффициенты s_j,k и d_j,k содердат информацию о составе сигнала на разных масштабах и вычисляются по формулам:

, (2.2)

. (2.3)

Однако при этом компьютерные расчеты занимают довольно длительное время, т.к. при вычислении приходится проводить O(N² ) операций, где N – число имеющихся значений функции. Опишем более быстрый алгоритм.

В реальных ситуациях с оцифрованным сигналом мы всегда имеем дело с конечным набором цифр (точек). Поэтому всегда существует наилучший уровень разрешения, когда каждый интервал содержит по одному числу. Соответственно и суммирование по k будет идти в конечных пределах. Удобно изменить шкалу разрешения (или шкалу f), приписав значение j=0 этому наилучшему уровню разрешения. В этом случае легко вычислить вейвлеткоэффициенты для более усредненных уровней j³1. Многомасштабный анализ приводит естественным путем к иерархической и быстрой схеме вычисления вейвлеткоэффициентов заданной функции.

В общем случае итерационные формулы быстрого вейвлетпреобразования имеют вид:

, (2.4)

(2.5)

с

. (2.6)

Эти уравнения обеспечивают быстрые (или пирамидальные) алгоритмы вычисления вейвлеткоэффициентов, поскольку требуют только O(N) операций для своего завершения. Начав с s_0,k , мы вычислим все другие вейвлеткоэффициенты, если параметры вейвлета h_m и g_m известны. Явный вид вейвлета при этом не используется. Простая форма полученных итерационных уравнений служит единственным оправданием введения множителя в функциональное уравнение (1.8). В принципе, коэффициенты h_m и g_m можно было бы перенормировать. Однако, уравнения (2.4), (2.5) используются на практике значительно чаще других, и поэтому эту нормировку не изменяют. Любые дополнительные сомножители в них могут привести лишь к усложнению численных расчетов.

Остающиеся проблемы связаны с начальными данными. Если известен явный вид функции f(x), то коэффициенты s_0,k можно вычислить, используя формулу (2.6). Но ситуация отличается от этой, если доступны только дискретные значения f(x). Чтобы достичь высокой точности, хорошо бы задать очень малые интервалы (плотную решетку), но это зачастую недоступно изза конечности интервалов сбора информации. В таком случае простейшее принимаемое решение состоит в непосредственном использовании величин f(k) из доступного набора данных в виде коэффициентов s_0,k и применении быстрого вейвлетпреобразования с использованием формул (2.4), (2.5). Это безопасная операция, т.к. пирамидальный алгоритм обеспечивает полную реконструкцию сигнала, а коэффициенты s_0,k по сути представляют собой локальные средние значения сигнала, взвешенные со скейлингфункцией.

В общем случае можно выбрать

. (2.7)

Рассмотренная ситуация отвечает условию s_0,k =f(k), что соответствует c_m =d_0m .

Обратное быстрое вейвлетпреобразование позволяет реконструировать функцию по значениям ее вейвлеткоэффициентов.

3. Двумерные вейвлеты

Многомасштабный анализ можно проводить и с многомерными функциями. Существует два способа обобщить его на двумерный случай, но чаще используется построение, заданное тензорными произведениями.

Тривиальный путь построения двумерного ортонормального базиса исходя из одномерного ортонормального вейвлетбазиса y_j,k (x)=2^j/2 y(2^j xk) состоит в том, чтобы путем тензорного произведения образовать соответствующие функции из двух одномерных базисов:

. (3.1)

В этом базисе две переменных x₁ и x₂ сжимаются поразному.

Больший интерес для многих приложений имеет другая конструкция, в которой масштабирование полученного ортонормального вейлетбазиса происходит по обеим переменным одинаковым образом и двумерные вейвлеты задаются следующим выражением:

Учебная работа № 1208. Матричные операции в вейвлетном базисе