Учебная работа № 1335. Некоторые главы мат. анализа
Некоторые главы мат анализа
ГЛАВА 1 РЯДЫ И ИНТЕГРАЛ ФУРЬЕ
Основные сведения
Функция f (x ), определенная на всей числовой оси называется периодической , если существует такое число ![]() , что при любом значении х выполняется равенство
, что при любом значении х выполняется равенство ![]() . Число Т называется периодом функции.
. Число Т называется периодом функции.
Отметим некоторые с в о й с т в а этой функции:
1) Сумма, разность, произведение и частное периодических функций периода Т есть периодическая функция периода Т .
2) Если функция f (x ) период Т , то функция f (ax )имеет период ![]() .
.
3) Если f (x ) периодическая функция периода Т , то равны любые два интеграла от этой функции, взятые по промежуткам длины Т (при этом интеграл существует), т. е. при любых a и b справедливо равенство 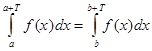 .
.
Тригонометрический ряд. Ряд Фурье
Если f (x ) разлагается на отрезке ![]() в равномерно сходящийся тригонометрический ряд:
в равномерно сходящийся тригонометрический ряд:
![]()
![]()
,то это разложение единственное и коэффициенты определяются по формулам:
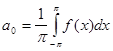
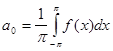
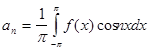
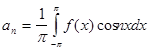
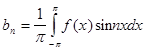
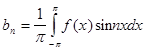
Тригонометрический ряд (1) рассмотренного вида с коэффициентами называется тригонометрическим рядом Фурье , а ![]()
![]()
Достаточные признаки разложимости функции в ряд Фурье
Точка ![]()
![]()
![]()
![]()
![]()
ТЕОРЕМА 1 (Дирихле). Если ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ТЕОРЕМА 2. Если f (x ) периодическая функция с периодом ![]()
![]()
![]()
![]()
![]()
![]()
Ряды Фурье для четных и нечетных функций
Пусть f (x ) четная функция с периодом 2L , удовлетворяющая условию f (x ) = f (x ) .
Тогда для коэффициентов ее ряда Фурье находим формулы:
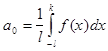
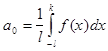
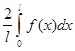
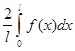
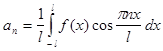
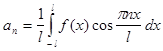
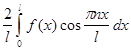
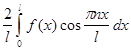
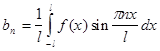
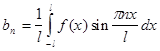
![]()
![]()
![]()
Таким образом, в ряде Фурье для четной функции отсутствуют члены с синусами, и ряд Фурье для четной функции с периодом 2L выглядит так:
![]()
![]()
Пусть теперь f (x ) нечетная функция с периодом 2L , удовлетворяющая условию f (x ) = f (x ).
Тогда для коэффициентов ее ряда Фурье находим формулы:
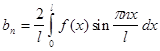
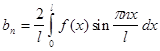
Таким образом, в ряде Фурье для нечетной функции отсутствует свободный член и члены с косинусами, и ряд Фурье для нечетной функции с периодом 2L выглядит так:
![]()
![]()
Если функция f (x ) разлагается в тригонометрический ряд Фурье на промежутке![]()
![]()
![]()
![]()
![]()
, где![]()
![]()
![]()
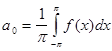
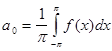
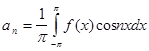
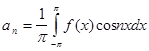
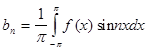
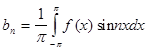
Если f (x ) разлагается в тригонометрический ряд Фурье на [0,L ], то доопределив заданную функцию f (x ) соответствующим образом на [L, 0]; далее периодически продолжив на (T =2L ), получим новую функцию, которую разлагаем в тригонометрический ряд Фурье.
Для разложения в ряд Фурье непериодической функции, заданной на конечном произвольном промежутке [a ,b ], надо : доопределить на [b ,a +2L ] и периодически продолжить, либо доопределить на [b 2L ,a ] и периодически продолжить.
Ряд Фурье по любой ортогональной системе функций
Последовательность функций ![]()
![]()
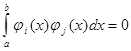
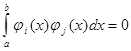
![]()
![]()
Система называется ортогональной и нормированной (ортонормированной) на отрезке [a,b],
если выполняется условие
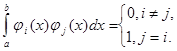
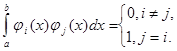
Пусть теперь f (x ) любая функция непрерывная на отрезке [a ,b ]. Рядом Фурье такой функции f (x ) на отрезке [a ,b ] по ортогональной системе называется ряд:
![]()
![]()
коэффициенты которого определяются равенством:
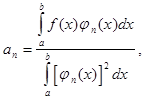
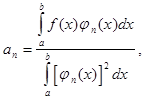
Если ортогональная система функций на отрезке [a ,b ] ортонормированная, то в этом случаи
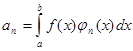
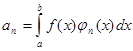
Пусть теперь f (x ) любая функция, непрерывная или имеющая конечное число точек разрыва первого рода на отрезке [a ,b ]. Рядом Фурье такой функции f (x ) на томже отрезке
по ортогональной системе называется ряд:
![]()
![]()
Если ряд Фурье функции f (x ) по системе (1) сходится к функции f (x ) в каждой ее точке непрерывности, принадлежащей отрезку [a ,b ]. В этом случае говорят что f (x ) на отрезке [a ,b ] разлагается в ряд по ортогональной системе (1).
Комплексная форма ряда Фурье
Выражение ![]()
![]()
![]()
![]()
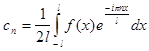
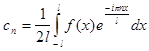
![]()
![]()
Переход от ряда Фурье в комплексной форме к ряду в действительной форме и обратно осуществляется с помощью формул:
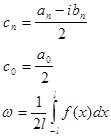
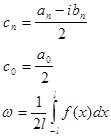
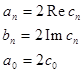
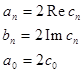
Задача о колебании струны
Пусть в состоянии равновесия натянута струна длинной l с концами x= 0 и x =l . Предположим, что струна выведена из состояния равновесия и совершает свободные колебания. Будем рассматривать малые колебания струны, происходящие в вертикальной плоскости.
При сделанных выше допущениях можно показать, что функция u (x,t ) , характеризующая положение струны в каждый момент времени t, удовлетворяет уравнению
![]()
![]()
Наша з а д а ч а найти функцию u (x,t ) , график которой дает форму струны в любой момент времени t , т. е. найти решение уравнения (1) при граничных:
![]()
![]()
и начальных условиях:
![]()
![]()
Сначала будем искать решения уравнения (1), удовлетворяющие граничным условиям(2). Нетрудно увидеть, что u (x ,t )![]()
![]()
![]()
![]()
![]()
![]()
Подстановка выражения (4) в уравнение (1) дает:
![]()
![]()
Из которого наша задача сводится к отысканию решений уравнений:
![]()
![]()
Используя это условие X (0)=0, X (l )=0, докажем, что ![]()
![]()
a) Пусть ![]()
![]()
![]()
![]()
![]()
![]()
откуда ![]()
![]()
![]()
![]()
б) Пусть ![]()
![]()
![]()
![]()
![]()
![]()
получим ![]()
![]()
![]()
![]()
в) ![]()
![]()
![]()
![]()
![]()
![]()
Уравнения имеют корни :
![]()
![]()
получим:
![]()
![]()
![]()
![]()
где ![]()
![]()
![]()
![]()
откуда ![]()
![]()
![]()
![]()
![]()
![]()
Учитывая это, можно записать:
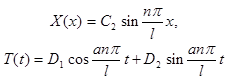
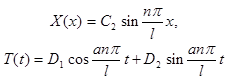
и, следовательно
![]()
![]()
но так как A и B разные для различных значений n то имеем
![]()
![]()
где ![]()
![]()
![]()
![]()
Итак, подчиним функцию u (x,t ) начальным условиям, т. е. подберем ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Эти равенства являются соответственно разложениями функций ![]()
![]()
![]()
![]()
![]()
![]()
где
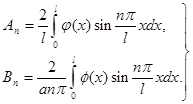
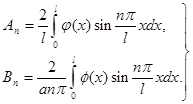
Интеграл Фурье
Достаточные условия представимости функции в интеграл Фурье.
Для того, чтобы f (x ) была представлена интегралом Фурье во всех точках непрерывности и правильных точках разрыва, достаточно:
1) абсолютной интегрируемости на ![]()
![]()
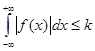
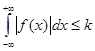
2) на любом конечном отрезке [L , L ] функция была бы кусочногладкой
3) в точках разрыва функции, ее интеграл Фурье определяется полусуммой левого и правого пределов в этих точках, а в точках непрерывности к самой функции f (x )
Интегралом Фурье функции f(x) называется интеграл вида:
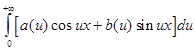
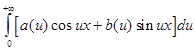
, где 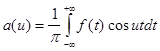
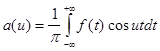
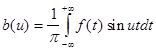
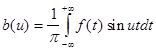
Интеграл Фурье для четной и нечетной функции
Пусть f (x )четная функция, удовлетворяющая условиям представимости интегралом Фурье.
Учитывая, что 

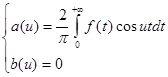
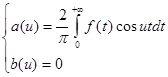
Таким образом, интеграл Фурье четной функции f (x ) запишется так:
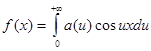
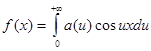
где a (u ) определяется равенством (3).
Рассуждая аналогично, получим, для нечетной функции f (x ) :
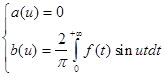
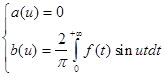
и, следовательно, интеграл Фурье нечетной функции имеет вид:
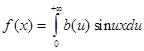
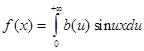
где b (u ) определяется равенством (4).
Комплексная форма интеграла Фурье
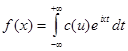
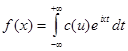
где
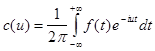
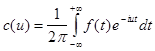
Выражение в форме (5) является комплексной формой интеграла Фурье для функции f (x ).
Если в формуле (5) заменить c (u ) его выражением, то получим:
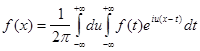
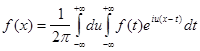
Фуpье в комплексной форме. Переход от интеграла Фурье в комплексной форме к интегралу
в действительной форме и обратно осуществим с помощью формул:
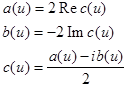
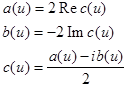
Формулы дискретного преобразования Фурье
Обратное преобразование Фурье.
![]()
![]()
![]()
![]()
где n =1,2,… , k =1,2,…
Дискретным преобразованием Фурье называется N мерный вектор ![]()
![]()
![]()
![]()
при этом, ![]()
![]()
Разложение четной функции в ряд
Данную выше функцию сделаем четной(см. теорию), и рассмотрим ее на промежутке от 0 до ![]()
![]()
![]()
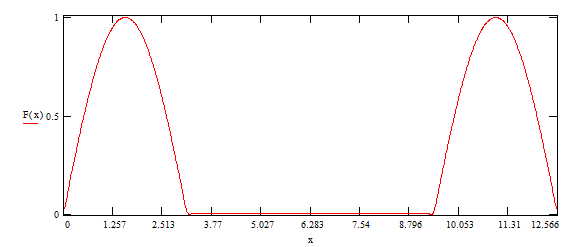

Рис.2
поэтому разложение по косинусу имеет вид:
![]()
![]()
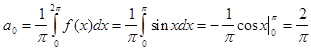
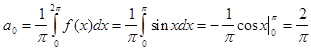
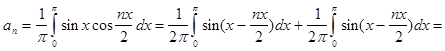
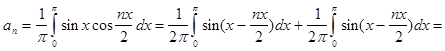
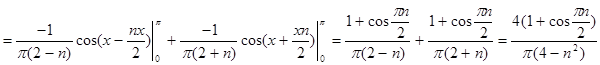
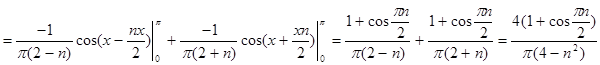
Из разложения видим что при n =2 дробь теряет смысл поэтому отдельно рассмотрим разложения первого и второго коэффициента суммы:
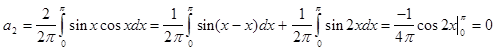
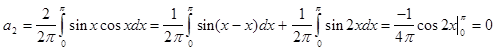
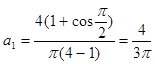
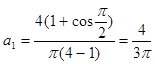
На основе данного разложения запишем функцию в виде ряда:
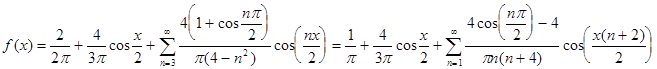
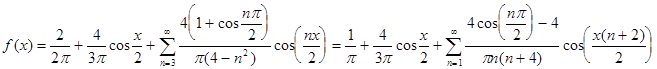
и вообще
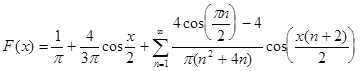
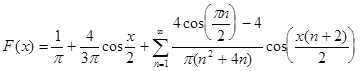
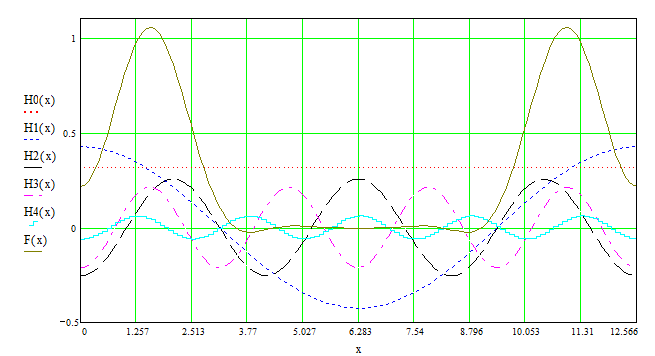
Найдем первые пять гармоник для найденного ряда:
1ая гармоника ![]()
![]()


2ая гармоника ![]()
![]()
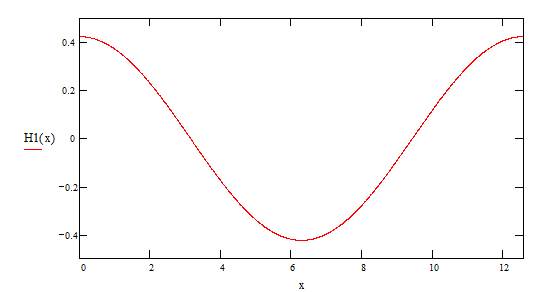

3я гармоника ![]()
![]()
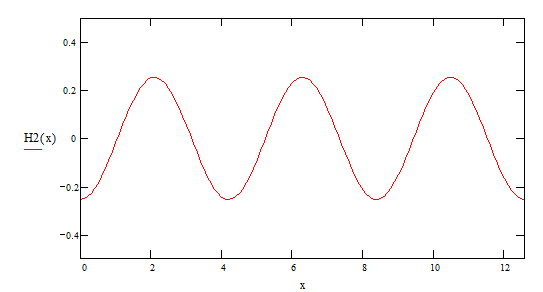

4ая гармоника ![]()
![]()
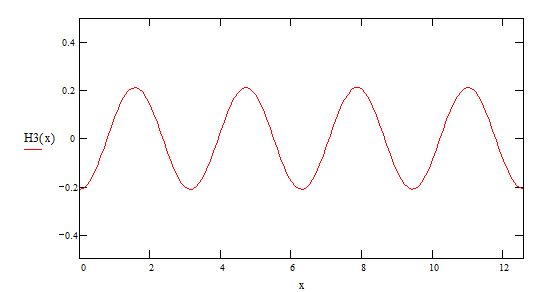

5ая гармоника ![]()
![]()
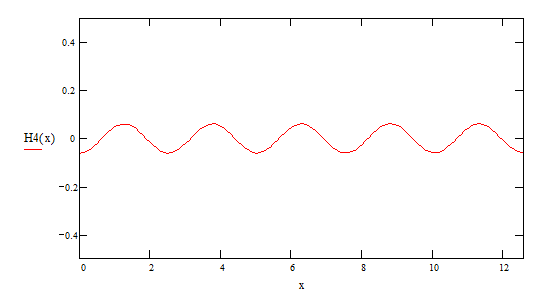

А теперь рассмотрим сумму этих гармоник F(x):

Комплексная форма ряда по косинусам
Для рассматриваемого ряда получаем коэффициенты (см. гл.1)
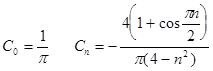
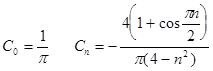
но при ![]()
![]()
![]()
![]()
![]()
![]()
и случай когда n =2:
![]()
![]()
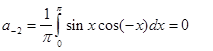
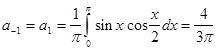
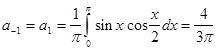
И вообще комплексная форма:
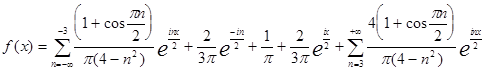
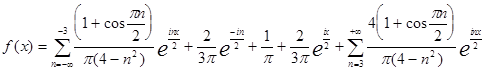
или
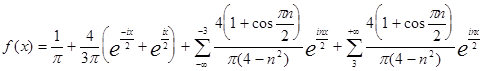
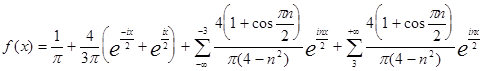
или
![]()
![]()


Разложение нечетной функции в ряд
Аналогичным образом поступаем с данной функцией F(x), продлевая ее как нечетную, и рассматриваем на промежутке от 0 до ![]()
![]()
![]()
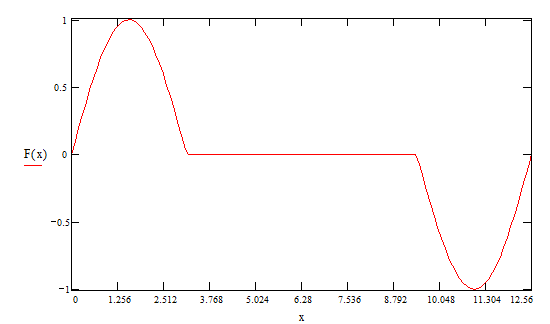

Рис.3
поэтому разложение по синусам имеет вид:
![]()
![]()
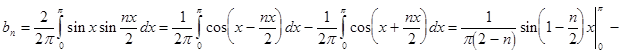
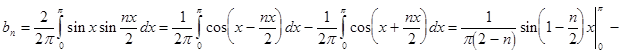
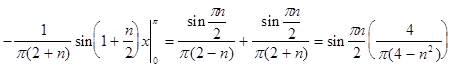
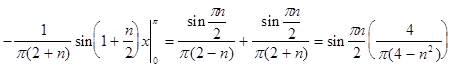
Из данного разложения видно, что при n =2 произведение неопределенно (можно не учесть часть суммы), поэтому рассмотрим два отдельных случая.
При n =1:
![]()
![]()
и при n =2:
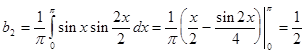
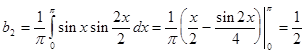
Учитывая данные коэффициенты имеем разложения в виде
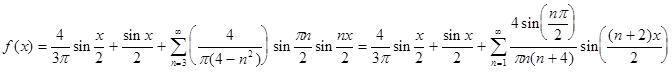
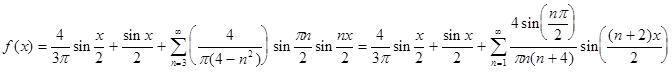
и вообще
![]()
![]()
Найдем первые пять гармоник для данного разложения:
1ая гармоника ![]()
![]()
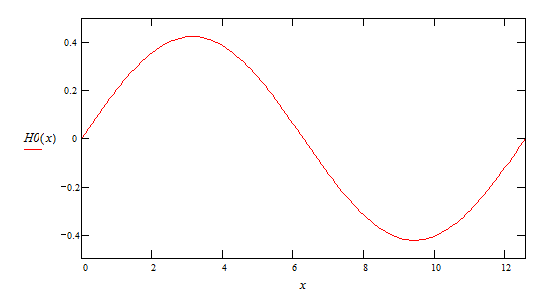

2ая гармоника ![]()
![]()
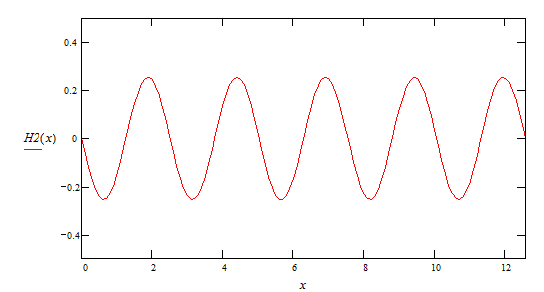

3ая гармоника ![]()
![]()
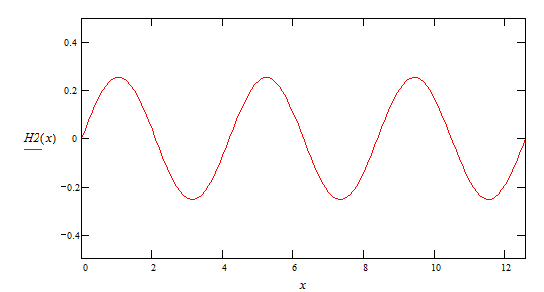

4ая гармоника ![]()
![]()
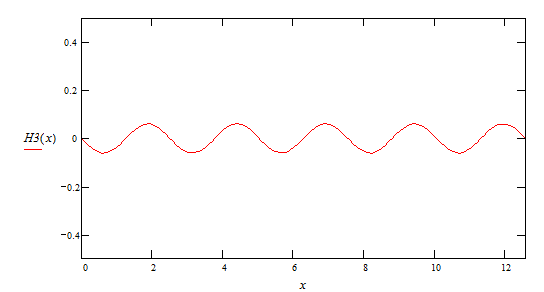

5ая гармоника ![]()
![]()
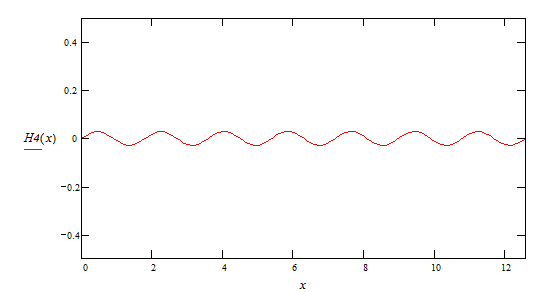

И просуммировав выше перечисленные гармоники получим график функции F (x )
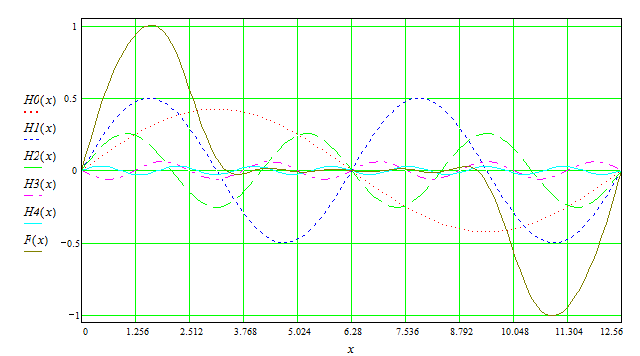

На основании главы 2, разложение функции в тригонометрический ряд(рис.1), разложение в ряд по косинусам(рис.2), разложение по синусам(рис.3), можно заключить, что данная функция разложима в тригонометрический ряд и это разложение единственное. И проанализировав суммы первых пяти гармоник по каждому разложению можно сказать, что наиболее быстрее к заданному графику достигается при разложении по синусам.
Комплексная форма ряда по синусам
Основываясь на теорию (см. гл.1) для ряда получаем:
![]()
![]()
![]()
![]()
![]()
![]()
тогда комплексный ряд имеет вид:
![]()
![]()
![]()
![]()
![]()
![]()
ГЛАВА 3 ПРЕДСТАВЛЕНИЕ ФУНКЦИИ ИНТЕГРАЛОМ ФУРЬЕ
Проверка условий представимости
Данную ранее функцию (см. гл. 2) доопределим на всей прямой от ![]()
![]()
![]()
![]()
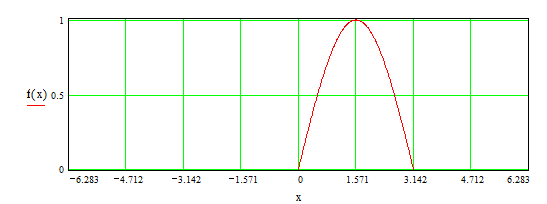

Рис.4
а) f(x)определенна на R;
б) f(x) возрастает на ![]()
![]()
![]()
![]()
f(x) = const на ![]()
![]()
![]()
![]()
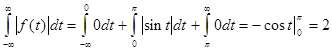
![]()
![]()
Интеграл Фурье
В соответствии с теорией (см. гл. 1) найдем a (u ) и b (u ):
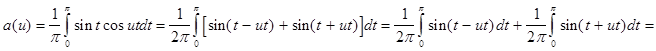
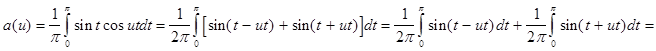
![]()
![]()
![]()
![]()
![]()
![]()
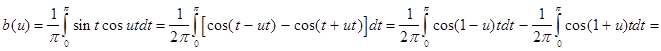
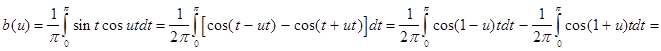
![]()
![]()
![]()
![]()
И в конечном варианте интеграл Фурье будет выглядеть так:
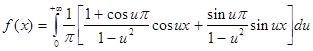
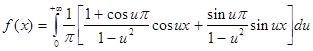
Интеграл Фурье в комплексной форме
Теперь представим интеграл Фурье в комплексной форме. На основе выше полученных разложений имеем:
![]()
![]()
![]()
![]()
а теперь получим интеграл в комплексной форме:
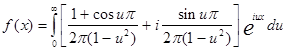
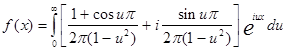
ГЛАВА 4 ПРЕДСТАВЛЕНИЕ ФУНКЦИИ ПОЛИНОМОМ ЛЕЖАНДРА
Основные сведения
Функцию можно разложить в ортонормированной системе пространства X=[1,1] , причем полиномы получим, если проинтегрируем выражение:
![]()
![]()
Соответственно получим для n=0,1,2,3,4,5, … :
![]()
![]()
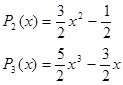
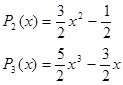
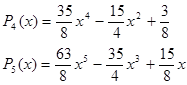
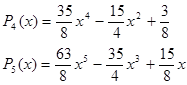
. . . . . . . . . .
Для представления функции полиномом Лежандра необходимо разложить ее в ряд:
![]()
![]()
где 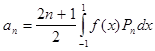
Преобразование функции
Наша первоначальная функция имеет вид (см. рис. 1):
![]()
![]()
т. к. она расположена на промежутке от 0 до ![]()
![]()
Замена:
![]()
![]()
и тогда F(t) примет вид
![]()
![]()
или
![]()
![]()
Вычисление коэффициентов ряда
Исходя из выше изложенной формулы для коэффициентов находим:
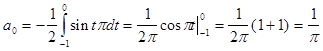
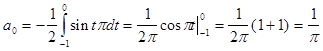
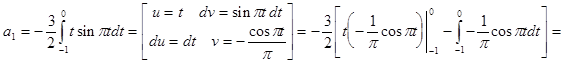
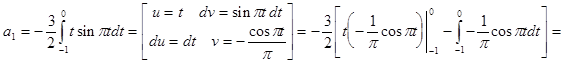
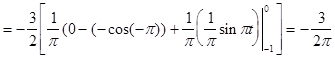
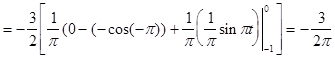
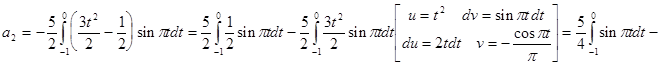
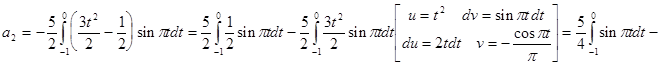
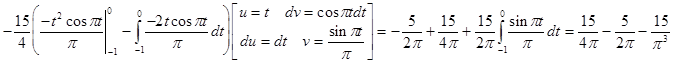
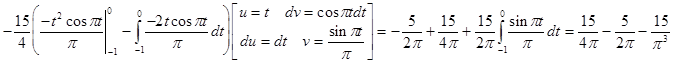
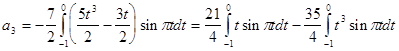
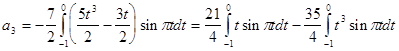
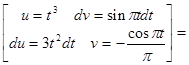
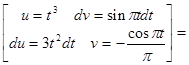
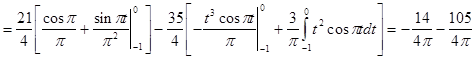
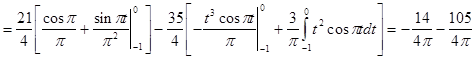
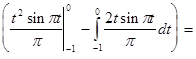
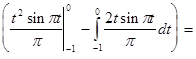
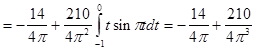
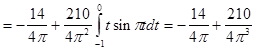
Далее вычисление коэффициентов осложнено, поэтому произведем вычисление на компьютере в системе MathCad и за одно проверим уже найденные:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
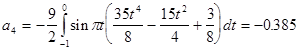
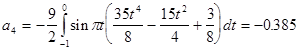
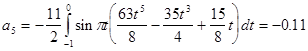
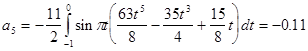
Рассмотрим процесс стремления суммы полинома прибавляя поочередно ![]()
![]()
![]()
![]()

![]()
![]()
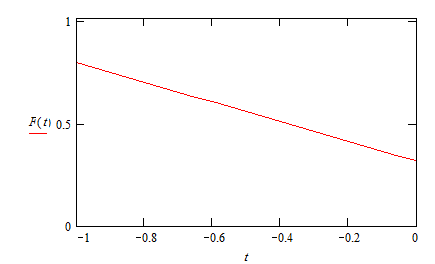

![]()
![]()
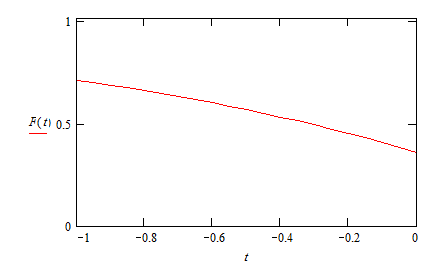

![]()
![]()
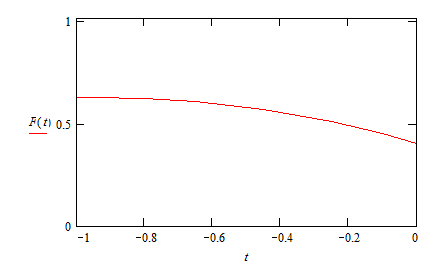

![]()
![]()
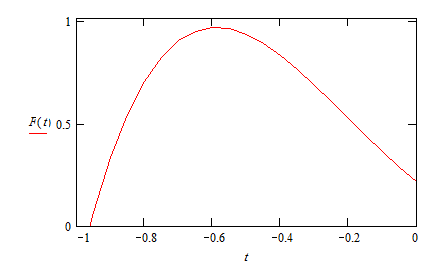

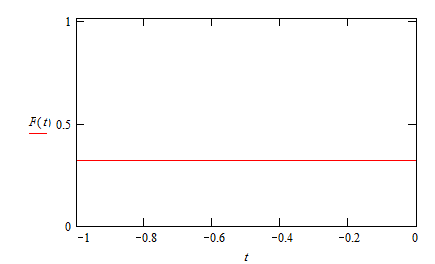
А теперь рассмотрим график суммы пяти полиномов F (t ) на промежутки от 1 до 0 (рис.5):
![]()
![]()
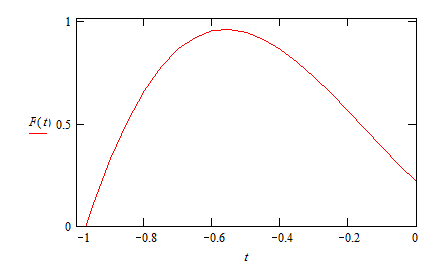

Рис. 5
т.к. очевидно, что на промежутке от 0 до 1 будет нуль.
Вывод:
На основе расчетов гл.2 и гл.4 можно заключить, что наиболее быстрое стремление из данных разложений к заданной функции достигается при разложении функции в ряд.
ГЛАВА 5 ДИСКРЕТНЫЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
Прямое преобразование
Для того, чтобы произвести прямое преобразование, необходимо задать данную функцию (гл. 1, рис. 1) таблично. Поэтому разбиваем отрезок от 0 до ![]()
![]()
![]()
![]()
В нашем случае ![]()
![]()
![]()
![]()
для нашего случая ![]()
![]()
Составим табличную функцию:
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 0.785 | 1.571 | 2.356 | 3.142 | 3.927 | 4.712 | 5.498 | |
| 0 | 0.707 | 1 | 0.707 | 0 | 0 | 0 | 0 |
Табл. 1
Прямым дискретным преобразованием Фурье вектора ![]()
![]()
![]()
![]()
![]()
![]()
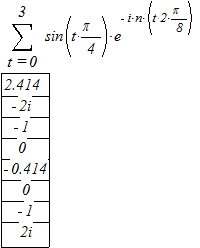
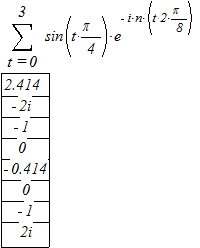
Сумму находим только до 3 слагаемого, т.к. очевидно, что от 4 до 7 к сумме суммируется 0 (т.к. значения функции из таблицы равны нулю).
Составим таблицу по прямому дискретному преобразованию:
зная, ![]()
![]()
![]()
![]()
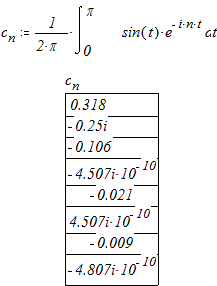
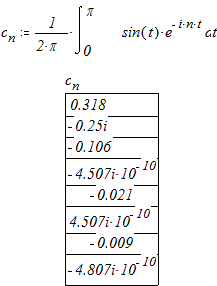
![]()
![]()
![]()
![]()
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 2,4 | 2 | 1 | 0 | 0.4 | 0 | 1 | 2 | |
| 0.318 | 0.25 | 0.106 | 0 | 0.021 | 0 | 0.009 | 0 |
Табл. 2
Амплитудный спектр ![]()
![]()
![]()
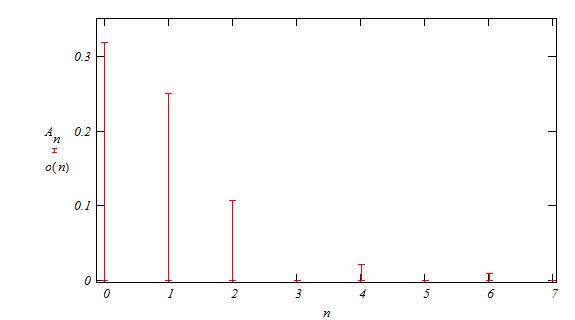

Обратное преобразование
Обратимся к теории гл.1. Обратное преобразование есть функция :
![]()
![]()
В нашем случаи это:
![]()
![]()


А теперь найдем модули ![]()
![]()
![]()
![]()
![]()
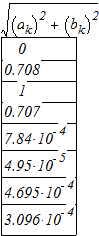
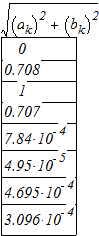
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 0.785 | 1.571 | 2.356 | 3.142 | 3.927 | 4.712 | 5.498 | |
| 0 | 0.707 | 1 | 0.707 | 0 | 0 | 0 | 0 | |
| 0 | 0.708 | 1 | 0.707 | 8e4 | 5e5 | 5e4 | 3e4 |
Табл. 3
Из приведенной таблицы видно, что ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Построим графики используя табл.3, где ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
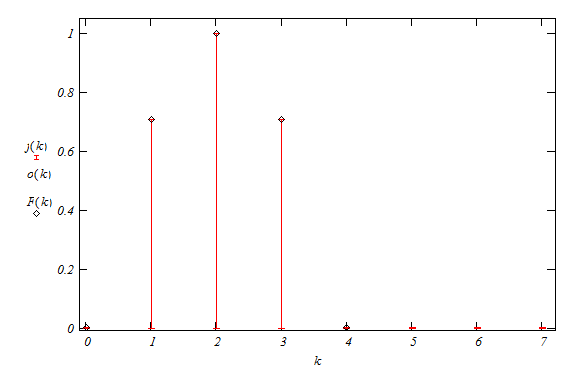

Рис. 6
Вывод:
На основе проделанных расчетов можно заключить, что заданная функция представима в виде тригонометрического ряда Фурье, а также интеграла Фурье, полинома Лежандра и дискретных преобразований Фурье. О последнем можно сказать, что спектр (рис. 6) прямого и обратного преобразований совпадают с рассматриваемой функцией и расчеты проведены правильно.
Этап I
1 Постановка задачи
Дана основная (рис. 1.1а) и резервная (рис. 1.1б) схемы. Рассмотреть два способа повышение надежности основной схемы до уровня 0.95
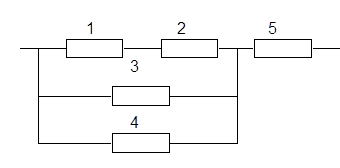
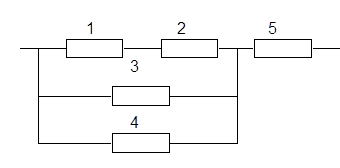
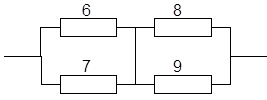
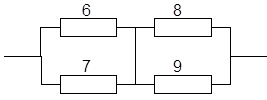
а) б)
Рис. 1.1
Первый способ
каждому элементу основной схемы подключаются параллельно по N резервных элементов имеющих надежность в два раза меньше, чем надежность элемента к которому подключают.
Второй способ
подключить к основной схеме параллельно по N резервной схеме.
| № элемента | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Надежность |
0.6 | 0.6 | 0.6 | 0.3 | 0.7 | 0.4 | 0.3 | 0.5 | 0.1 |
| Надеж.(резер.) |
0.3 | 0.3 | 0.3 | 0.15 | 0.35 |
2 Теоретическая часть
Ввиду важности операций сложения и умножения над событиями дадим их определение:
Суммой двух событий А и В называется событие С, состоящее в выполнении события А или события В , или обоих событий вместе.
Суммой нескольких событий называется событие, состоящее в выполнении хотя бы одного из этих событий.
Произведением двух событий А и В называется событие D , состоящее в совместном выполнении события А и события В .
Произведением нескольких событий называется событие, состоящее в совместном выполнении всех этих событий.
А к с и о м ы т е о р и и в е р о я т н о с т е й :
1. Вероятность любого события находится в пределах:
![]()
![]()
2. Если А и В несовместные события ![]()
![]()
![]()
![]()
3. Если имеется счетное множество несовместных событий А1 , А2 , … Аn , … ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Следствие: сумма вероятностей полной группы несовместных событий равна единице , т.е. если
![]()
![]()
![]()
![]()
![]()
![]()
![]()
то
![]()
![]()
Сумма вероятностей противоположных событий ровна единице :
![]()
![]()
Правило умножения вероятностей: вероятность произведения (пересечения, совмещения) двух событий равна вероятности одного из них, умноженной на условную вероятность второго при наличии первого
![]()
![]()
Для независимых событий правило умножения принимает вид:
![]()
![]()
![]()
![]()
Основываясь на теорию выведем некоторые формулы для решения поставленной задачи.
Схема состоит из нескольких n блоков (рис. 2.1), каждый из которых (независимо от других) может выйти из строя. Надежность каждого блока равна p . Безотказная работа всех без исключения блоков необходима для безотказной работы в целом. Найти вероятность безотказной работы всей схемы.
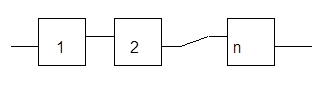
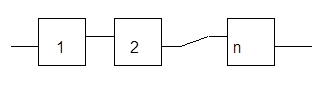
Рис. 2.1
Событие A ={безотказная работа прибора} есть произведение n независимых событий А 1 , А 2 , … Аn , где Ai ={безотказная работа i го блока}. По правилу умножения для независимых событий имеем
![]()
![]()
Схема состоит из 2 блоков (рис. 2.2), каждый из которых (независимо от друг от друга) может выйти из строя. Надежность каждого блока равна p . Найти вероятность безотказной работы всей системы.
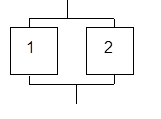
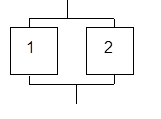
Рис. 2.2
От события В ={система будет работать} перейдем к противоположному:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
По правилу умножения для независимых событий:
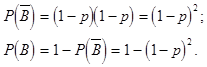
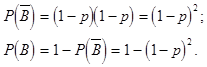
3 Практическая часть
Воспользовавшись выше изложенными формулами рассчитаем надежность основной схемы (рис. 1а), она составит :
![]()
![]()
, а также резервной схемы (рис. 1б) :
![]()
![]()
Рассмотрим первый способ подключения (смотри рис. 3.1), когда подключаем по N элементов до тех пор, пока ![]()
![]()
![]()
![]()
![]()
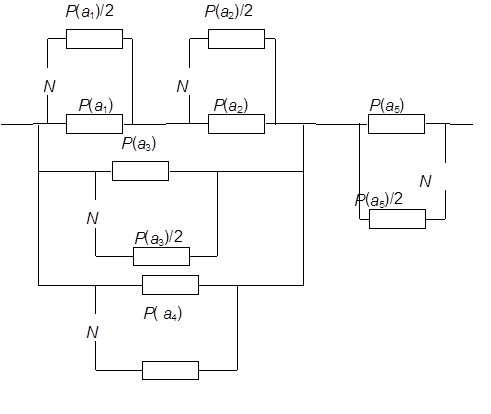
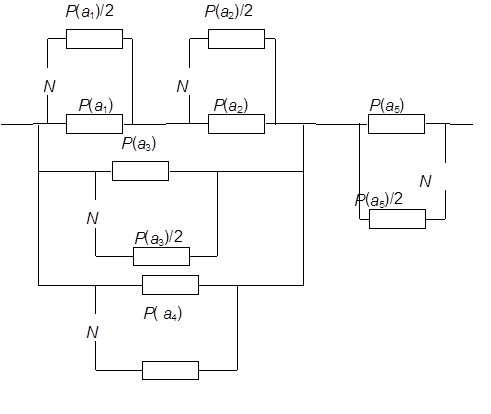
Рис. 3.1
Тогда формула вероятности для схемы на рис. 2 будет выглядеть так :
![]()
![]()
, где
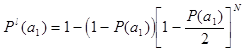
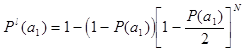
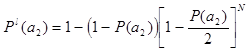
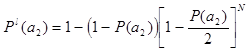
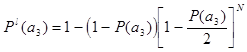
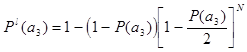
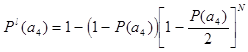
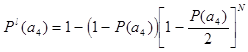
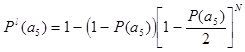
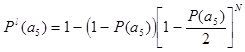
Увеличивая N дополнительных элементов пошагово добиваемся значения ![]()
![]()
![]()
![]()
![]()
Шаг первый, при N =1
![]()
![]()
Шаг второй, при N =2
![]()
![]()
Шаг третий, при N =3
![]()
![]()
Шаг четвертый, при N =4
![]()
![]()
Шаг пятый, при N =5
![]()
![]()
Из рассмотренных вычислений можно заключить, что для достижения заданной вероятности 0.95 необходимо пяти добавочных элементов.
Рассмотрим второй способ подключения к основной резервной схемы (рис. 3) и найдем число N подключений при котором достигается заданная вероятность ![]()
![]()
![]()
![]()
![]()
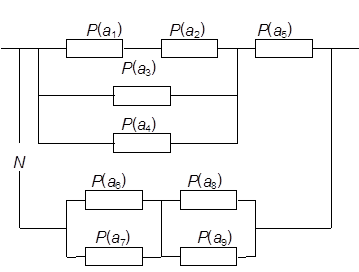
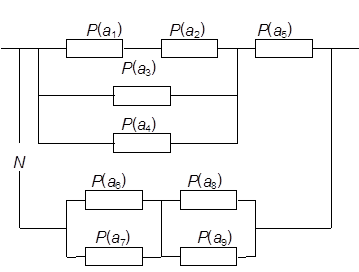
Рис. 3.2
Формула по которой будет вычисляться вероятность схемы на рис. 3 выглядит так :
![]()
![]()
, где
![]()
![]()
, а ![]()
![]()
Увеличивая N дополнительных резервных схем пошагово добиваемся значения ![]()
![]()
![]()
![]()
![]()
При N =1 : ![]()
![]()
При N =2 : ![]()
![]()
При N =3 : ![]()
![]()
При N =4 : ![]()
![]()
При N =5 : ![]()
![]()
При N =6 : ![]()
![]()
Из рассмотренных вычислений можно заключить, что для достижения заданной вероятности 0.95 необходимо шесть резервных схем.
Этап II
1 Постановка задачи
найти неизвестную константу функции f (x );
выписать функцию распределения, построить их графики;
найти математическое ожидание и дисперсию;
найти вероятность попадания в интервал (1;4).
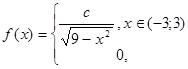
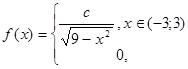
2 Теоретическая часть
Под случайной величиной понимается величина, которая в результате измерения (опыта) со случайным исходом принимает то или иное значение.
Функция распределения случайной величины Х называется вероятность того, что она примет значение меньшее, чем заданное х :
![]()
![]()
Основные свойства функции распределения:
1) F (x ) неубывающая функция своего аргумента, при ![]()
![]()
![]()
![]()
2) ![]()
![]()
3) ![]()
![]()
Плотностью распределения непрерывной случайной величины Х в точке х называется производная ее функции распределения в этой точке. Обозначим ее f (x ) :
![]()
![]()
Выразим функцию распределения F (x ) через плотность распределения f (x ):
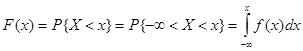
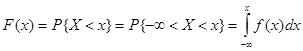
Основные свойства плотности распределения f (x ):
1. Плотность распределения неотрицательная функция ![]()
![]()
2. Интеграл в бесконечных пределах от плотности распределения равен единицы:
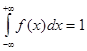
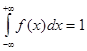
Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных ее значений на вероятности этих значений.
![]()
![]()
Перейдем от дискретной случайной величины Х к непрерывной с плотностью f (x ).
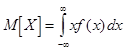
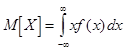
Дисперсия случайной величины есть математическое ожидание квадрата соответствующей центрированной величины:
![]()
![]()
Для непосредственного вычисления дисперсии непрерывной случайной величины служит формула:
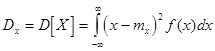
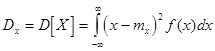
3 Практическая часть
Для нахождения неизвестной константы c применим выше описанное свойство:
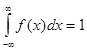
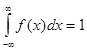
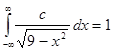
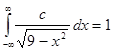
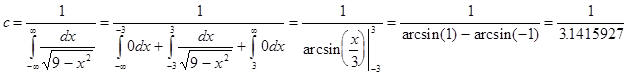
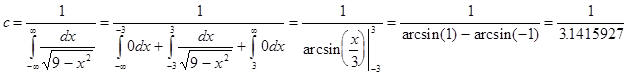

 (5 оценок, среднее: 4,60 из 5)
(5 оценок, среднее: 4,60 из 5)