Учебная работа № 1270. Двойной интеграл в механике и геометрии

Учебная работа № 1270. Двойной интеграл в механике и геометрии

Министерство общего и профессионального образования Р.Ф.

Иркутский государственный технический университет.

Кафедра высшей математики.

Реферат.

Применение двойных интегралов к задачам механики и геометрии.

Выполнила: студентка

группы ТЭ971

Мелкоступова С.С.

Проверил преподаватель

кафедры высшей математики

Седых Е.И.

Иркутск 1998.

Содержание.

1.Объём цилиндрического тела. Двойной интеграл.

2. Вычисление двойных интегралов.

a) примеры.

3.Приложения двойных интегралов к задачам механики.

а) масса плоской пластинки переменной плотности.

б) статические моменты и центр тяжести пластинки.

в) моменты инерции пластинки.

4.Вычисление площадей и объёмов с помощью двойных интегралов.

а) Объём.

б) Вычисление площади плоской области.

5.Вычисление площади поверхности.

а) Примеры.

1.Объём цилиндрического тела. Двойной интеграл.

Цилиндрическим телом называется тело, ограниченное плоскостью Oxy, поверхностью, с которой любая прямая, параллельная оси Oz, пересекается не более чем в одной точке, и цилиндрической поверхностью, образующая которой параллельна оси Oz.

Область D, высекаемая в плоскости Oxy цилиндрической поверхностью, называется основанием цилиндрического тела (см. рис.1). В частных случаях боковая цилиндрическая поверхность может и отсутствовать; примером тому служит тело, ограниченное плоскостью Oxy и верхней полусферой .

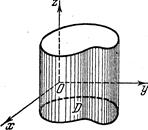
Рис. 1

Обычно тело можно составить из некоторого числа цилиндрических тел и определить искомый объект как сумму объёмов цилиндрических тел, составляющих это тело.

Прежде всего напомним два принципа, из которых мы исходим при определении объёма тела:

1) если разбить тело на части, то его объём будет равен сумме объёмов всех частей;

2) объём прямого цилиндра, т.е. цилиндрического тела, ограниченного плоскостью, параллельной плоскости Oxy, равен площади основания, умноженной на высоту тела.

Пусть есть уравнение поверхности, ограничивающей цилиндрическое тело. Будем считать функцию непрерывной в области D и сначала предположим, что поверхность целиком лежит над плоскостью Oxy, т.е. что всюду в области D.

Рис. 2

Обозначим искомый объем цилиндрического тела через V, Разобьем основание цилиндрического тела область D на неко­торое число n областей произвольной формы; будем называть их частич­ными областями. Пронумеровав частичные области в какомнибудь порядке, обозначим их через а их площади через . Через границу каждой частичной области проведем цилинд­рическую поверхность с образующей, параллельной оси Oz. Эти цилиндри­ческие поверхности разрежут поверх­ность на n кусков, соответствующих n частичным областям. Таким образом, цилиндрическое тело окажется разби­тым на n частичных цилиндрических тел (см.рис.2). Выберем в каждой частичной области произвольную точку и заменим соответствующее частичное цилиндрическое тело прямым цилинд­ром с тем же основанием и высотой, равной . В ре­зультате получим nступенчатое тело, объем которого равен

Принимая объем V данного цилиндрического тела приближенно равным объему построенного nступенчатого тела, будем считать, что V_n тем точнее выражает V, чем больше n и чем меньше каждая из частичных областей. Переходя к пределу при мы будем требовать, чтобы не только площадь каждой частичной области стремилась к нулю, но чтобы стремились к нулю все ее размеры. Если назвать диаметром области наибольшее расстояние между точками ее границы (Например, диаметр прямоугольника равен его диагонали, диаметр эллипса—его большой оси. Для круга приведенное определение диаметра равносильно обычному.), то высказанное требование будет означать, что каждый из диаметров частичных областей должен стремиться к нулю; при этом сами области будут стягиваться в точку (Если известно только, что площадь области стремится к нулю, то эта область может и не стягиваться в точку. Например, площадь прямо­угольника с постоянным основанием и высотой, стремящейся к нулю, стремится к нулю, а прямоугольник стягивается к своему основанию, т. е. к отрезку).

В соответствии со сказанным мы принимаем искомый объем V равным пределу, к которому стремится Vn при стремлении к нулю наибольшего диаметра частичных областей (при этом):

К отысканию предела подобных сумм для функций двух перемен­ных приводят самые разнообразные задачи, а не только задача об объеме.

Рассмотрим этот вопрос в общем виде. Пусть любая функция двух переменных (не обязательно положительная), не­прерывная в некоторой области D, ограниченной замкнутой линией. Разобьем область D на частичные, как указано выше, выберем в каждой частичной области по произвольной точке и составим сумму

(*)

где значение функции в точке ; и , площадь ча­стичной области.

Сумма (*) называется nй интегральной суммой для функции в области D, соответствующей данному разбиению этой области на n частичных областей.

Определение. Двойным интегралом от функции по области D называется предел, к которому стремится n я интегральная сумма ( * ) при стремлении к нулю наибольшего диаметра частичных областей.

­Записывается это так:

Читается: “двойной интеграл от на по области D”. Выражение , показывающее вид суммируемых слагаемых, называется подынтегральным выражением; функция назы­вается подынтегральной функцией, элементом площади, об­ласть D областью интегрирования, наконец, переменные x и у на­зываются переменными интегрирования.

Таким образом, можно сказать, что объем цилиндрического тела, ограниченного плоскостью Oxy, поверхностью и цилиндрической поверхностью с образующей, параллельной оси Oz, выражается двойным интегралом от функции , взятым по области, являющейся основанием цилиндрического тела:

.

Аналогично теореме существования обыкновенного интеграла имеет место следующая теорема.

Теорема существования двойного интеграла.

Если функция непрерывна в области D, ограниченной замкнутой линией , то её n я интегральная сумма стремится к пределу при стремлении к нулю наибольшего диаметра частичных областей . Этот предел , т . е . двойной интеграл , не зависит от способа разбиения области D на частичные области и от выбора в них точек P_i .

Двойной интеграл, разумеется, представляет собой число, зависящее только от подынтегральной функции и области интегрирования и вовсе не зависящее от обозначений переменных интегрирования, такчто, например,

.

Далее мы убедимся а том, что вычисление двойного интеграла может быть произведено посредством двух обыкновенных интегрирований.

2.Вычисление двойных интегралов.

При вычислении двойного интеграла элемент площади нам удобно представить в ином виде. Будем разбивать область интегрирования D в плоскости Oxy на частичные области посредством двух систем координатных линий: x=const, y=const. Этими линиями служат прямые, параллельные соответственно оси Oy и оси Ox, а частичными областями прямоугольники со сторонами, параллельными осям координат. Ясно, что площадь каждой частичной области будет равна произведению соответствующих и . Поэтому элемент площади мы запишем в виде т.е. элемент площади в декартовых координатах является произведением дифференциалов независимых переменных. Мы имеем

. (*)

При вычислении двойного интеграла (*) мы будем опираться на тот факт, что он выражает объём V цилиндрического тела с основанием D, ограниченного поверхностью . Напомним, что мы уже занимались задачей об объёме тела, когда рассматривали применения определённого интеграла к задачам геометрии и получили формулу

(**)

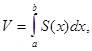
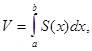
Рис.3

где S(х) площадьпоперечногосечения тела плоскостью, перпендикулярной к оси абсцисс, а и уравнения плоскостей,ограничивающих тело. Применим теперь этуформулу к вычислениюдвойного интеграла

Предположим сначала, что область интегрирова­ния D удовлетворяет сле­дующему условию: любаяпрямая, параллельная оси Ox или Oy, пересекаетграницу области не более чем в двухточках. Соответствующее цилиндрическое тело изоб­ражено нарис.3

Область D заключимвнутрь прямоугольника

стороны которого касаются границы области в точках А, В, С, Е. Интервал [а, b] является ортогональной проекцией области D на ось Ох, а интервал [c, d] ортогональной проекцией облас­ти D на ось Oy. На рис.5 область D показана в плоско­сти Оху.

Точками A и C граница разбивается на две линии: ABC и AEC, каждая из которых пересекается с любой прямой, параллельной оси Oy, в одной точке. Поэтому, их уравнения можно записать в форме, разрешенной относительно y:

(ABC),

(AEC).

Аналогично точками В и Е граница разбивается на линии ВАЕи ВСЕ, уравнения которых можно записать так:

(BAE),

(BCE).

Рис.5

Рассечем рассматриваемое цилиндрическое телопроизвольнойплоскостью, параллельной плоскости Oyz, т.е.x=const, (рис). В сечении мы получим криволинейнуютра­пецию PMNR, площадь которой выражается интеграломот функции , рассматри­ваемой как функция одной пе­ременной у, причем у изменя­ется от ординаты точки P до ординаты точки R. Точка Pесть точка входа прямой х =const (в плоскости Оху ) в область D, а R точка ее выхода из этой области. Из уравнений линий АВС и АЕС следует, что ординаты этих точек при взятом х соот­ветственно равны и .

Следовательно, интеграл

дает выражение для площади плоского сечения PMNR. Ясно, что величина этого интеграла зависит от выбранного значения х; другими словами, площадь рассматриваемого поперечного сечения является некоторой функцией от х, мы обозначим ее через S(х):

Согласно формуле (**) объем всего тела будет равен интег­ралу от S(x) в интервале изменения .( При выводе формулы (**) мы считали, что S(*) есть геометриче­ская площадь поперечного сечения. Поэтому дальнейшие рассуждения справедливы, строго говоря, лишь для случая . Основываясь на уточненном геометрическом смысле двойного интеграла, нетрудно до­казать, на чем мы не будем останавливаться, что получающаяся формула для вычисления двойного интеграла будет верна для любых функций.

Заменяя в этой формуле S(x) её выражением, окончательно получим

или в более удобной форме

(А)

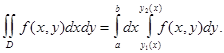
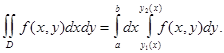
Пределы внутреннего интеграла переменные; они указывают границы изменения переменной интегрирования у при постоянном значении второго аргумента х. Пределы внешнего интеграла постоянны; они указывают границы, в которых может изменяться аргумент х.

Меняя роли х и у, т. е. рассматривая сечения тела плоскостями y=const , мы найдем сначала, что площадь Q(у) такого сечения равна , где у при интегрировании считаетсявеличиной постоянной. Интегрируя затем Q(у) в пределах измене­ния у, т. е. от c до d, мы придем ко второму выражению для двойного интеграла

(Б)

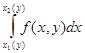
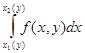
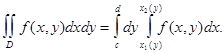
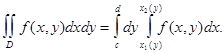
Здесь интегрирование совершается сначала по х, а потом по у.

.Формулы (А) и (Б) показывают, что вычисление двойного ин­теграла сводится к последовательному вычислению двух обыкно­венных определенных интегралов; нужно только помнить, что во внутреннем интеграле одна из переменных принимается при интегрировании за постоянную. Для краткости правые части фор­мул (А) и (Б) называют повторными (или двукратными) интегра­лами, а сам процесс расстановки пределов интегрирования при­ведением двойного интеграла к повторному.

Формулы приведения двойного интеграла к повторному приобре­тают особенно простой вид, когда область D является прямоуголь­ником со сторонами, параллельными осям координат (рис.6). В этом случае становятся постоянными пределы не только внеш­него, но и внутреннего интегралов:

В других случаях для сведения двойного интеграла к повтор­ному необходимо прежде всего построить область интегрирования;лучше всего изобразить эту область прямо в плоскости Оху, как это сделано на рис. Затем нужно установить порядок интегрирования, т. е. наметить, по какой переменной будет про­изводиться внутреннее интегрирование, а по какой внешнее, и расставить пределы интегрирования.

Поясним на примерах, какпроизводится расстановка пределов интегрирования.

а) Примеры.

1) Приведем к повторному двойной интеграл если область D треугольник,

Рис. 6. Рис. 7.

ограниченныйпрямыми y=0,y=x и х=а (рис.7). Если интегрировать сна­чала по у, а потом по х, то внутреннее интегрирование произво­дится от линии у=0 до линии у=х, а внешнее от точки х=0 до точки х=а. Поэтому

Меняя порядок интегрирования, получим

2) Приведем к повторному интеграл если область D ограничена линиями у=0, у=х² и х+у=2.

Область D, а также координаты крайних ее точек показаны на рис. 158. Вид области указывает на то, что удобнее интегрироватьсначала по x, а потом по y:

Если изменим порядок интегрирования, то результат уже не удастся записать в виде одного повторного интеграла, так как линия OBA имеет на разных участках разные уравнения.

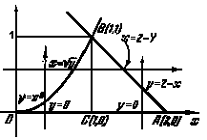
Рис.8

Разбивая область D на две : OBC и CBA, получим

Этот пример показывает, как важно с самого начала продумать порядок интегрирования.

Формулы (А) и (Б) сведения двойного интеграла к повторному справедливы и для случая областей более общего вида. Так, формула (А) применима к области, указанной на рис.9, а формула (Б) к области, изображенной на рис.10. В случае области ещё более общего вида (Рис.11) двойной интеграл следует разбить на сумму интегралов по более простым областям, а затем каждый из них сводить отдельно к повторному, пользуясь формулами (А) и (Б).

Рассмотрим теперь несколько примеров, связанных с вычислением двойных интегралов.

Примеры. 1) Найдём двойной интеграл от функции

по прямоугольной области D

Геометрически I выражает объём четырёхугольной призмы

(рис.12), основанием которой служит прямоугольник D, усечённый плоскостью .

Возьмём повторный интеграл сначала по y, затем по x:

То же самое получим, интегрируя сначала по x, а затем по y:

2) Вычислим двойной интеграл

по области D, ограниченной линиями y=x и y=x² . Область D

изображена на рис.13. Интегрируя сначала по y, а потом по x,

получаем

Правильность результата можно проверить, изменив порядок интегрирования :

Вычислим объём тела, ограниченного цилиндрическими поверхностями и плоскостью z=0 (рис.14,а).

Поверхность, ограничивающая тело сверху, имеет уравнение z=4y² . Область интегрирования D получается в результате пересечения параболы с линией пересечения цилиндра z=4y² и плоскости z=0, т.е. с прямой y=2 (Рис. 14, б). Ввиду симметрии тела относительно плоскости Oyz вычисляем половину искомого объёма :

Следовательно, куб.ед.

4) Вычислим объём V тела, ограниченного поверхностью и плоскостью Oxy.

Заданное тело представляет собой сегмент эллиптического

параболоида, расположенный над плоскостью Оху (рис.15). Параболоид пересекается с плоско­стью Оху по эллипсу

Следовательно, задача состоит в отыскании объема цилиндрического тела, имеющего своим основанием внутренность указанного эллипса и ограниченного параболоидом

В силу симметрии тела относи­тельно плоскостей Oxz и Oyz можно вычислить объем четвертой его части, заключенной в первом координатном угле. Этот объем равен двойному интегралу, распространенному по области, заданной условиями т. е. по четверти эллипса. Интегрируя сначала по у, затем по х, получим

Подстановка даёт

откуда

3.Приложения двойных интегралов к задачам

механики.

а) Масса плоской пластинки переменной плотности.

Рассмотрим тонкую пластинку, расположенную на плос­кости Оху и занимающую область D. Толщину этой пластинки считаем настолько малой, что изменением плотности по толщине ее можно пренебречь.

Поверхностной плотностью такой пластинки в данной точке назы­вается предел отношения массы площадки к ее площади при условии, что площадка стягивается к данной точке.

Определенная таким образом поверхностная плотность будет зависеть только от положения данной точки, т. е. являться функ­цией ее координат:

Если бы плотность была постоянной (), то масса всей пластинки равнялась бы , где S площадь пластинки. Найдем теперь массу неоднородной пластинки, считая, что ее плотность является заданной функцией . Для этого разобьем область, занимаемую пластинкой, на частичные области с площадями (рис. 16). Выбирая в каждой частичной области произвольную точку , будем считать, что плотность во всех точках частичной области постоянна и равна плотнос­ти в выбранной точке. Составим приближенное выражение для массы пластинки в виде интег­ральной суммы

(*)

Для точного выражения массы следует найти предел суммы (*) при условии и каждая частичная область стягивается к точке. Тогда

б) Статические моменты и центр тяжести пластинки.

Перейдём теперь к вычислению статических моментов рассматриваемой пластинки относительно осей координат. Для этого сосредоточим в точках массы соответствующих частич­ных областей и найдем статические моменты полученной сис­темы материальных точек :

Переходя к пределу при обычных условиях и заменяя интегральные суммы интегралами, получим

Находим координаты центра тяжести :

Если пластинка однородна, т.е. то формулы упрощаются :

где S площадь пластинки.

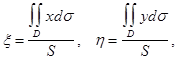
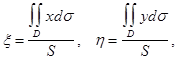
в) Моменты инерции пластинки.

Моментом инерции материальной точки Р с массой m относительно какойлибо оси называется произведение массы на квадрат расстояния точки Р от этой оси.

Метод составления выражений для моментов инерции пластинки относительно осей координат совершенно такой же, какой мы применяли для вычисления статических моментов. Приведем поэтому только окончательные результаты, считая, что :

Отметим еще, что интеграл называется центробежным моментом инерции; он обозначается .

В механике часто рассматривают полярный момент инерции точки, равный произведению массы точки на квадрат ее расстояния до данной точки полюса. Полярный момент инерции пластинки относительно начала координат будет равен

4. Вычисление площадей и объёмов с помощью двойных интегралов.

а) Объём.

Как мы знаем, объем V тела, ограничен­ного поверхностью , где неотрицательная функ­ция, плоскостью и цилиндрической поверхностью, направ­ляющей для которой служит граница области D, а образующие параллельны оси Oz, равен двойному интегралу от функции по области D :

Пример 1. Вычислить объем тела, ограниченного поверхностями x=0, у=0, х+у+ z=1, z =0 (рис. 17).

Рис.17Рис.18

Решение. D заштрихованная на рис. 17 треугольная область в плоскости Оху, ограниченная прямыми x=0, у=0, x+y=1. Расставляя пределы в двойном интеграле, вычислим объем:

Итак, куб. единиц.

Замечание 1 . Если тело, объем которого ищется, ограни­чено сверху поверхностью а снизу—поверхностью , причем проекцией обеих поверхностей на пло­скость Оху является область D, то объем V этого тела равен разности объемов двух “цилиндрических” тел; первое из этих цилиндрических тел имеет нижним основанием область D, а верх­ним поверхность второе тело имеет нижним осно­ванием также область D, а верхним поверхность (рис.18).

Поэтому объём V равен разности двух двойных интегралов :

или

(1)

Легко, далее, доказать, что формула (1) верна не только в том случае, когда и неотрицательны, но и тогда, когда и любые непрерывные функции, удовлетворяющие соотношению

Замечание 2 . Если в области D функция меняет знак, то разбиваем область на две части: 1) область D₁ где 2) область D₂ ,где . Предположим, что области D₁ и D₂ таковы, что двойные интегралы по этим обла­стям существуют. Тогда интеграл по области D₁ будет положи­телен и будет равен объему тела, лежащего выше плоскости Оху. Интеграл по D₂ будет отрицателен и по абсолютной величине равен объему тела, лежащего ниже плоскости Оху, Следовательно, интеграл по D будет выражать раз­ность соответствующих объемов.

б) Вычисление площади плоской области.

Если мы со­ставим интегральную сумму для функции по области D, то эта сумма будет равна площа­ди S,

при любом способе разбиения. Пере­ходя к пределу в правой части равен­ства, получим

Если область D правильная , то площадь выразится двукратным интегралом

Производя интегрирование в скобках, имеем, очевидно, Пример 2. Вычислить площадь области, ограниченной кривыми Рис.19 Решение. Определим точки пересечения данных кривых (Рис.19). В точке пересечения ординаты равны, т.е. , отсюда Мы получили две точки пересечения Следовательно, искомая площадь

5. Вычисление площади поверхности.

Пусть требуется вычислить площадь поверхности, ограниченной линией Г (рис.20); поверхность задана уравнением где функция непрерывна и имеет непрерывные частные производные. Обозначим проекцию линии Г на плоскость Oxy через L. Область на плоскости Oxy, ограниченную линией L, обозначим D.

Разобьём произвольным образом область D на n элементарных площадок В каждой площадке возьмём точку Точке P_i будет соответствовать на поверхности точка Через точку M_i проведём касательную плоскость к поверхности. Уравнение её примет вид

(1)

На этой плоскости выделим такую пло­щадку , которая проектируется на плоскость Оху в виде площадки . Рассмотрим сумму всех площадок

Предел этой суммы, когда наибольший из диаметров пло­щадок стремится к нулю, мы будем называть площадью по­верхности, т. е. по определению положим

(2)

Займемся теперь вычислением площади поверхности. Обозна­чим через угол между касательной плоскостью и плоскостью Оху.

Рис.20 Рис.21

На основании известной формулы аналитической геометрии можно написать (рис.21)

или

(3)

Угол есть в то же время угол между осью Oz и перпендикуляром к плоскости (1). Поэтому на основании уравнения (1) и формулы аналитической геометрии имеем

Следовательно,

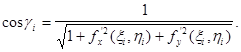
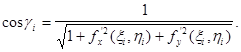
Подставляя это выражение в формулу (2), получим

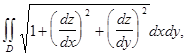
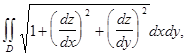
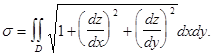
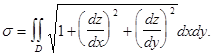
Так как предел интегральной суммы, стоящей в правой части последнего равенства, по определению представляет собой двойной интеграл то окончательно получаем

(4)

Это и есть формула, по которой вычисляется площадь поверхности

Если уравнение поверхности дано в виде или в виде то соответствующие формулы для вычисления поверхности имеют вид

(3^’ )

(3^’’ )

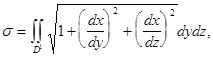
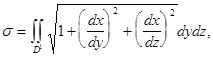
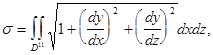
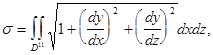
где D^’ и D^’’ области на плоскостях Oyz и Oxz, в которые проектируется данная поверхность.

а) Примеры.

Пример 1. Вычислить поверхность сферы

Решение. Вычислим поверхность верхней половины сферы (рис.22). В этом случае

Следовательно, подынтегральная функция примет вид

Область интегрирования определяется условием . Таким образом, на основании формулы (4) будем иметь

Для вычисления полученного двойного интеграла перейдём к полярным координатам. В полярных координатах граница области интегрирования определяется уравнением Следовательно,

Пример2. Найти площадь той части поверхности цилиндра которая вырезается цилиндром

Рис.22 Рис.23

Решение. На рис.23 изображена часть искомой поверхности. Уравнение поверхности имеет вид ; поэтому

Область интегрирования представляет собой четверть круга, т.е. определяется условиями

Следовательно,

Список использованной литературы.

1. А.Ф. Бермант ,И.Г. Араманович

Краткий курс математического анализа для втузов: Учебное пособие для втузов: М.: Наука, Главная редакция физикоматематической литературы , 1971 г.,736с.

2. Н.С. Пискунов

Дифференциальное и интегральное исчисления для втузов, Том 2:

Учебное пособие для втузов.13е изд. М. :Наука, Главная редакция физикоматематической литературы, 1985.560с.

3. В.С. Шипачёв

Высшая математика: Учебное пособие для втузов: М: Наука,

Главная редакция физикоматематической литературы.

Учебная работа № 1270. Двойной интеграл в механике и геометрии