Учебная работа № 1196. Алгоритм компактного хранения и решения СЛАУ высокого порядка
ВВЕДЕНИЕ.
Метод конечных элементов является численным методом для дифференциальных уравнений, встречающихся в физике [1]. Возникновение этого метода связано с решением задач космических исследований (1950 г.). Впервые он был опубликован в работе Тернера, Клужа, Мартина и Топпа. Эта работа способствовала появлению других работ; был опубликован ряд статей с применениями метода конечных элементов к задачам строительной механики и механики сплошных сред. Важный вклад в теоретическую разработку метода сделал в 1963 г. Мелош, который показал, что метод конечных элементов можно рассматривать как один из вариантов хорошо известного метода РэлеяРитца. В строительной механике метод конечных элементов минимизацией потенциальной энергии позволяет свести задачу к системе линейных уравнений равновесия [2,3].
Одной из существующих трудностей, возникающих при численной реализации решения контактных задач теории упругости методом конечных элементов (МКЭ), является решение систем линейных алгебраических уравнений (СЛАУ) большого порядка вида
![]()
Большинство существующих методов решения таких систем разработаны в предположении того, что матрица A имеет ленточную структуру, причем ширина ленты ![]() , где n2 порядок
, где n2 порядок![]() . Однако, при использовании МКЭ для численного решения контактных задач возможны случаи, когда ширина ленты
. Однако, при использовании МКЭ для численного решения контактных задач возможны случаи, когда ширина ленты ![]() [5].
[5].
1 ОБЗОР МЕТОДОВ РЕШЕНИЯ СЛАУ, ВОЗНИКАЮЩИХ В МКЭ
Основная идея метода конечных элементов состоит в том, что любую непрерывную величину, такую, как температура, давление и перемещение, можно аппроксимировать дискретной моделью, которая строится на множестве кусочнонепрерывных функций, определенных на конечном числе подобластей. Кусочнонепрерывные функции определяются с помощью значений непрерывной величины в конечном числе точек рассматриваемой области [1,2,3].
В общем случае непрерывная величина заранее неизвестна и нужно определить значения этой величины в некоторых внутренних точках области. Дискретную модель, однако, очень легко построить, если сначала предположить, что числовые значения этой величины в каждой внутренней точке области известны. После этого можно перейти к общему случаю. Итак, при построении конкретной модели непрерывной величины поступают следующим образом:
1. В рассматриваемой области фиксируется конечное число точек. Эти точки называются узловыми точками или просто узлами.
2. Значение непрерывной величины в каждой узловой точке считается переменной, которая должна быть определена.
3. Область определения непрерывной величины разбивается на конечное число подобластей, называемых элементами. Эти элементы имеют общие узловые точки и в совокупности аппроксимируют форму области.
4 .Непрерывная величина апроксимируется на каждом элементе функцией, которая определяется с помощью узловых значений этой величины. Для каждого элемента определяется своя функция, но функции подбираются таким образом, чтобы сохранялась непрерывность величины вдоль границ элемента.
Для решения СЛАУ в МКЭ требуется выбрать метод решения. Окончательное решение о применении итерационных или прямых методов решения СЛАУ необходимо принимать на основе анализа структуры исследуемой математической задачи. Прямые методы решения СЛАУ более выгодно использовать, если необходимо решать много одинаковых систем с различными правыми частями, или если матрица А не является положительноопределенной. Кроме того, существуют задачи с такой структурой матрицы, для которой прямые методы всегда предпочтительнее, чем итерационные.
1.1 Точные методы решения СЛАУ
Рассмотрим ряд точных методов решения СЛАУ [4,5].
Решение систем nлинейных уравнении с nнеизвестными по формулам Крамера.
Пусть дана система линейных уравнений, в которой число уравнений равно числу неизвестных:
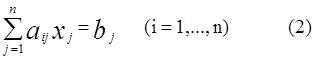
Предположим, что определитель системы d не равен нулю. Если теперь заменить последовательно в определителе столбцы коэффициентов при неизвестных хj столбцом свободных членов bj , то получатся соответственно n определителей d1 ,…,dn .
Теорема Крамера. Система n линейных уравнений с n неизвестными, определитель которой отличен от нуля, всегда совместна и имеет единственное решение, вычисляемое по формулам:
x1=d1/d; x2=d2/d;….; xn1=dn1/d; xn=dn/d;
Решение произвольных систем линейных уравнений.
Пусть
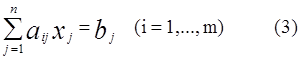
произвольная система линейных уравнений, где число уравнений системы не равно числу n неизвестных. Предположим, что система (3) совместна и r![]() min{m,n}, тогда в матрицах А и А найдутся r линейно независимых строк, а остальные mr строк окажутся их линейными комбинациями. Перестановкой уравнений можно добиться того, что эти r линейно независимых строк займут первые r мест.
min{m,n}, тогда в матрицах А и А найдутся r линейно независимых строк, а остальные mr строк окажутся их линейными комбинациями. Перестановкой уравнений можно добиться того, что эти r линейно независимых строк займут первые r мест.
Отсюда следует, что любое из последних m r уравнений системы (3) можно представить как сумму первых r уравнений (которые называются линейно независимыми или базисными),взятых с некоторыми коэффициентами. Тогда система эквивалентна следующей системе r уравнений с n неизвестными
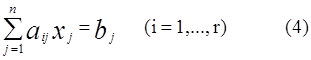
Предположим, что минор rго порядка, составленный из коэффициентов при первых r неизвестных, отличен от нуля Мr ![]() 0, т. е. является базисным минором. В этом случае неизвестные, коэффициенты при которых составляют базисный минор, называются базисными неизвестными, а остальные n r свободными неизвестными.
0, т. е. является базисным минором. В этом случае неизвестные, коэффициенты при которых составляют базисный минор, называются базисными неизвестными, а остальные n r свободными неизвестными.
В каждом из уравнений системы (4) перенесем в правую часть все члены со свободными неизвестными xr+1,…, xn. Тогда получим систему, которая содержит r уравнений с r базисными неизвестными. Так как определитель этой системы есть базисный минор Mr то система имеет единственное решение относительно базисных неизвестных, которое можно найти по формулам Крамера. Давая свободным неизвестным произвольные числовые значения, получим общее решение исходной системы.
Однородная система линейных уравнений.
Пусть дана однородная система линейных уравнений n неизвестными
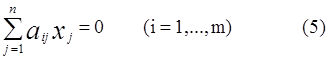
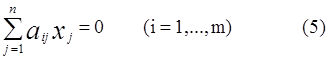
Так как добавление столбца из нулей не изменяет ранга матрицы системы, то на основании теоремы Кронекера Kaneлли эта система всегда совместна и имеет, по крайней мере, нулевое решение. Если определитель системы (5) отличен от нуля и число уравнений системы равно числу неизвестных, то по теореме Крамера нулевое решение является единственным.
В том случае, когда ранг матрицы системы (5) меньше числа неизвестных, т. е. r (А)< n, данная система кроме нулевого решения будет иметь и ненулевые решения. Для нахождения этих решений в системе (5) выделяем r линейно независимых уравнений, остальные отбрасываем. В выделенных уравнениях в левой части оставляем r базисных неизвестных, а остальные n r свободных неизвестных переносим в правую часть. Тогда приходим к системе, решая которую по формулам Крамера, выразим r базисных неизвестных x1 ,…, хr через n r свободных неизвестных.
Система (5) имеет бесчисленное множество решений. Среди этого множества есть решения, линейно независимые между собой.
Фундаментальной системой решений называются n r линейно независимых решений однородной системы уравнений.
Метод главных элементов.
Пусть дана система n линейных уравнений с n неизвестными
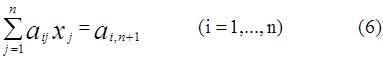
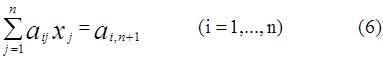
расширенная матрица системы (6) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Далее к каждой неглавной iй строке прибавим главную строку, умноженную на соответствующий множитель mi ; для этой строки.
В результате получим новую матрицу, все элементы qго столбца которой, кроме apq , состоят из нулей.
Отбросив этот столбец и главную pю получим новую матрицу, число строк и столбцов которой на единицу меньше. Повторяем те же операции с получившейся матрицей, после чего получаем новую матрицу и т.д.
Таким образом, построим последовательность матриц, последняя из которых является двучленной матрицейстрокой (главной строкой). Для определения неизвестных xi объединяем в систему все главные строки, начиная с последней.
Изложенный метод решения системы линейных уравнений с n неизвестными называется методом главных элементов. Необходимое условие его применения состоит том, что определитель матрицы не равен нулю [6,7].
Схема Халецкого.
Пусть система линейных уравнений дана в матричном виде.
Ax=b (7)
Где А квадратная матрица порядка n, а x,b векторы столбцы.
Представим матрицу А в виде произведения нижней треугольной матрицы С и верхней треугольной матрицы В с единичной диагональю, т.е.
А=СВ,
Где
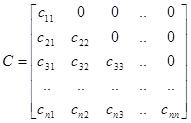
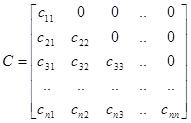
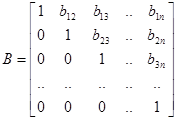
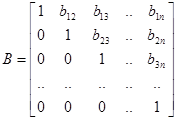
Причем элементы сij и bij определяются по формулам:
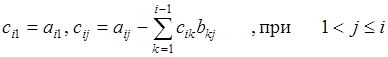
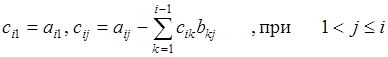
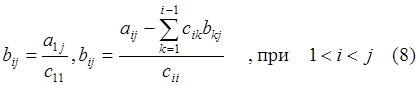
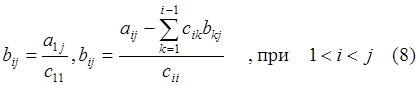
Уравнение (7) можно записать в следующем виде:
CBx=b. (9)
Произведение Bx матрицы B на векторстолбец x является векторомстолбцом, который обозначим через y:
Bx=y.(10)
Тогда уравнение (9) перепишем в виде:
Cy=b. (11)
Здесь элементы сij известны, так как матрица А системы (7) считается уже разложенной на произведение двух треугольных матриц С и В.
Перемножив матрицы в левой части равенства (11), получаем систему уравнений из которой получаем следующие формулы для определения неизвестных:
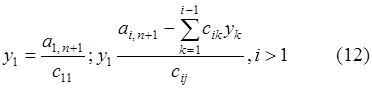
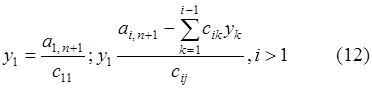
неизвестные yi удобно вычислять вместе с элементами b

 (3 оценок, среднее: 4,67 из 5)
(3 оценок, среднее: 4,67 из 5)