Учебная работа № 1195. Разбиения выпуклого многоугольника

Учебная работа № 1195. Разбиения выпуклого многоугольника

П.1. Выпуклый многоугольник с n сторонами можно разбить на треугольники диагоналями, которые пересекаются лишь в его вершинах. Вывести формулу для числа таких разбиений.

Определение: назовем правильным разбиением выпуклого nугольника на треугольники диагоналями, пересекающимися только в вершинах nугольника.

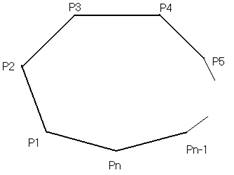
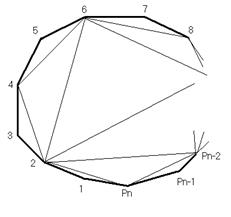
Пусть P₁ , P₂ , … ,P_n –вершины выпуклого nугольника, А_n число его правильных разбиений. Рассмотрим диагональ многоугольника P_i P_n .В каждом правильном разбиение P₁ P_n принадлежит какомуто треугольнику P₁ P_i P_n , где1<i<n. Следовательно, полагая i=2,3, … , n1, мы получаем (n2) группы правильных разбиений, включающие все возможные случаи.

Пусть i=2 – одна группа правильных разбиений, которая всегда содержит диагональ P₂ P_n .Число разбиений, входящих в эту группу совпадает с числом правильных разбиений (n1) угольника P₂ P₃ …Pn, то есть равно А_n1 .

Пусть i=3 – одна группа правильных разбиений, которая всегда содержит диагональ P₃ P₁ и P₃ P_{n .} Следовательно, число правильных разбиений, входящих в эту группу, совпадает с числом правильных разбиений (n2)угольника P₃ P₄ …Pn, то есть равно А_n2.

При i=4 среди треугольников разбиение непременно содержит треугольник P₁ P₄ P_n .К нему примыкают четырехугольник P₁ P₂ P₃ P₄ и (n3)угольник P₄ P₅ …Pn.Число правильных разбиений четырехугольника равно A_4, число правильных разбиений (n3) угольника равно

А_n3. Следовательно, полное число правильных разбиений, содержащихся в этой группе, равно

А_n3 A_4. Группы с i=4,5,6,… содержат А_n4 A_5, А_n5 A_6, … правильных разбиений.

При i=n2 число правильных разбиений в группе совпадает с числом правильных разбиений в группе с i=2,то есть равно А_n1.

Поскольку А₁ =А₂ =0, А₃ =1, A₄ =2 и т.к. n³ 3, то число правильных разбиений равно:

А _n= А _n1 +А _n2 +А _n3 A₄ +А _n4 A₅ + … + A ₅ А _n4 + A₄ А _n3 + А _n2 + А _n1.

Например:

A ₅ = A₄ + А₃ + A₄ =5

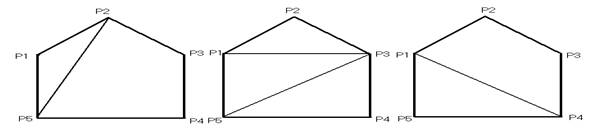
A₆ = A₅ + А₄ + А₄ + A₅ =14

A₇ = A₆ + А₅ + А_{4 *} А₄ +А₅ + A₆ =42

A₈ = A₇ + А₆ +А_5* А₄ + А_4* А₅ +А₆ + A₇ =132

П.2.1. Найдем количество во всех диагоналей правильных разбиениях, которые пересекают внутри только одну диагональ.

Проверяя на частных случаях, пришли к предположению, что количество диагоналей в выпуклых nугольниках равно произведению количества разбиений на (n3)

Докажем предположение, что P¹ _n =А_n (n3)

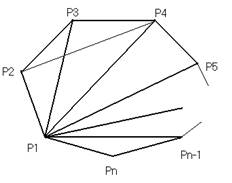
Каждый nугольник можно разбить на (n2) треугольника, из которых можно сложить (n3) четырехугольника, причем каждый четырехугольник будет иметь диагональ. Но в четырехугольнике можно провести 2 диагонали, значит в (n3) четырехугольниках можно провести (n3) дополнительные диагонали. Значит, в каждом правильном разбиении можно провести (n3) диагонали удовлетворяющих условию задачи.

П.2.2. Найдем количество во всех диагоналей правильных всех разбиениях, которые пересекают внутри только две диагонали.

Проверяя на частных случаях, пришли к предположению, что количество диагоналей в выпуклых nугольниках равно произведению количества разбиений на (n4), где n ≥ 5

Докажем предположение, что P² _n =(n4)А_{n ,} гдеn ≥ 5.

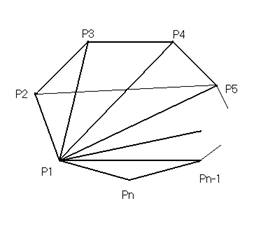
nугольник можно разбить на (n2) треугольников из которых можно сложить (n4) пятиугольника, в котором будут содержаться две непересекающиеся диагонали. Значит, найдется третья диагональ, которая пересекает две другие. Так как имеется (n4) пятиугольника, значит, существует (n4) дополнительные диагонали удовлетворяющих условию задачи.

П.2.3. Разбиение nугольника, в котором дополнительные диагонали пересекают главные k раз.

Определение 1 :Главными диагоналями выпуклого nугольника называются диагонали, которые разбивают его на треугольники, пересекаясь при этом только в вершинах nугольника.

Замечание: их существует (n3).

Определение 2 :Дополнительными диагоналями выпуклого nугольника называются диагонали, которые в данном разбиении пересекают главные диагонали.

Замечание: их существует менее (n3).

I.Определение k:

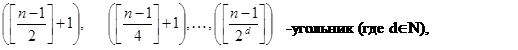Будем выделять из выпуклого nугольника

следующим образом: соединяем диагоналями через одну вершину данного nугольника, причем выделением считается получение последующего aугольника из предыдущего, используя не менее двух диагоналей. Выделение ведется до тех пор, пока не получится четырехугольник или треугольник (r = 4 или r = 3 (r – остаточный коэффициент)). Назовем каждое такое выделение циклом и введем величину, которая будет “считать” их (d). Для каждого d существует 2^d+1 многоугольников, первый многоугольник для данного d ,будет (2^d+1 +1)угольником. Для первой половины (для данного d) многоугольников r = 3, для второй r = 4. Последним многоугольником, для которого r = 3 будет (3×2^d )угольником. Окончательно получаем: r = 3, если nÎ[2^d+1 +1; 3×2^d ], в противном случае r = 4. За каждый цикл, если проводить дополнительные диагонали, будет добавляться по 2 пересечения и через d циклов число пересечений достигнет максимума в полученном данным способом разбиении. Обозначим это число буквой k.

Итак, за 1 цикл 2 пересечения, за 2 цикла – 4, за 3 – 6, очевидна арифметическая прогрессия с разностью 2, a1=2 и количество членов равным d; значит k=2+2(d1)=2d – только в том случае, если конечной фигурой окажется треугольник. В противном случае k=2d+1, так как четырехугольник имеет собственную диагональ.

Рассчитаем d: т.к.: d=1, n [2² +1; 2³ ]

d=2, n [2³ +1; 2⁴ ]

d=3, n [2⁴ +1; 2⁵ ]

…

Зависимость d от n логарифмическая по основанию 2; становится очевидным равенство: d=[log₂ (n1)]1. Выразим k через n:

k=2([log₂ (n1)]1), если nÎ[2^[log2(n1)] +1; 3×2^[log2(n1)]1 ]

или

k=2([log₂ (n1)]1)+1= 2[log₂ (n1)]1, если nÏ[2^[log2(n1)] +1; 3×2^[log2(n1)]1 ]

Так как k – максимум пересечений, то уместны неравенства:

k≤2([log₂ (n1)]1), если n Î [2^[log2(n1)] +1; 3 × 2^[log2(n1)]1 ]

или (*)

k≤2[log₂ (n1)]1, если n Ï [2^[log2(n1)] +1; 3 × 2^[log2(n1)]1 ]

II . Найдем число дополнительных диагоналей ( m), которые пересекают главные не более k раз.

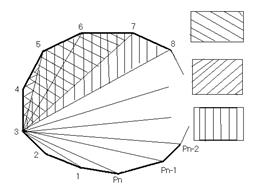
Выделим в данном выпуклом nугольнике (k+3)угольник (k+3)угольник (если это возможно), зн.

уже ‘использовано’ (n+3)2=k+1 всех

отбросили существующих треугольников

1 треугольник nугольника (всего их (n2)),потом добавили другой ‘отбросим’ крайний треугольник и реугольник и ‘добавим’ к получившейся фигуре еще опять получили один, имеющий общую с ней сторону, (k+3)угольник ‘не использованный’ треугольник, тогда останется (k+2) не использованных треугольника, и так далее до тех пор, пока не ‘используем’ все (n2)треугольника. Очевидна арифметическая прогрессия с разностью 1, a_m =n2 и c количеством членов равным m. Получим:n2=k+1+(m1)<=>n2=k+m<=>m=nk2m=n(k+2)Значит, в nугольник можно вписать (k+3)угольник (n(k+2))раз, то есть существуют такие (n(k+2)) дополнительные диагонали, которые пересекут k главных диагоналей.

Окончательно получаем: P^k _n =( n (k+2))А _{n ,} где(*).

Список литературы

Скращук Дмитрий (г. Кобрин). Разбиения выпуклого многоугольника

Учебная работа № 1195. Разбиения выпуклого многоугольника