Учебная работа № 1185. Теория вероятностей и математическая статистика

Учебная работа № 1185. Теория вероятностей и математическая статистика

Задача 1.

Генерация случайных чисел с заданным законом распределения с помощью случайных чисел, равномерно распределенных на интервале (0,1):

1. используя центральную предельную теорему, с помощью сумм 6 независимых равномерно распределенных на интервале (0,1) случайных чисел получить 25 случайных числа со стандартным нормальным законом распределения; найти выборочное среднее и выборочную дисперсию;

2. получить 11 случайных чисел с законом распределения Стьюдента с 10 степенями свободы; найти выборочное среднее и выборочную дисперсию.

Решение:

С помощью сумм 6 независимых равномерно распределенных на интервале (0,1) случайных чисел получим 24 случайных числа со стандартным нормальным законом распределения по формуле

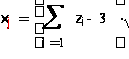, где z_i равномерно распределенные на интервале (0,1) случайные числа.

Получены следующие числа:

1.235	0.904	1.674	1.918	0.335
1.082	0.584	0.565	0.149	0.528
1.076	1.011	0.671	1.011	1.502
0.627	0.489	0.486	1.022	0.472
0.844	0.92	0.583	0.645	0.495

Найдем выборочное среднее по формуле

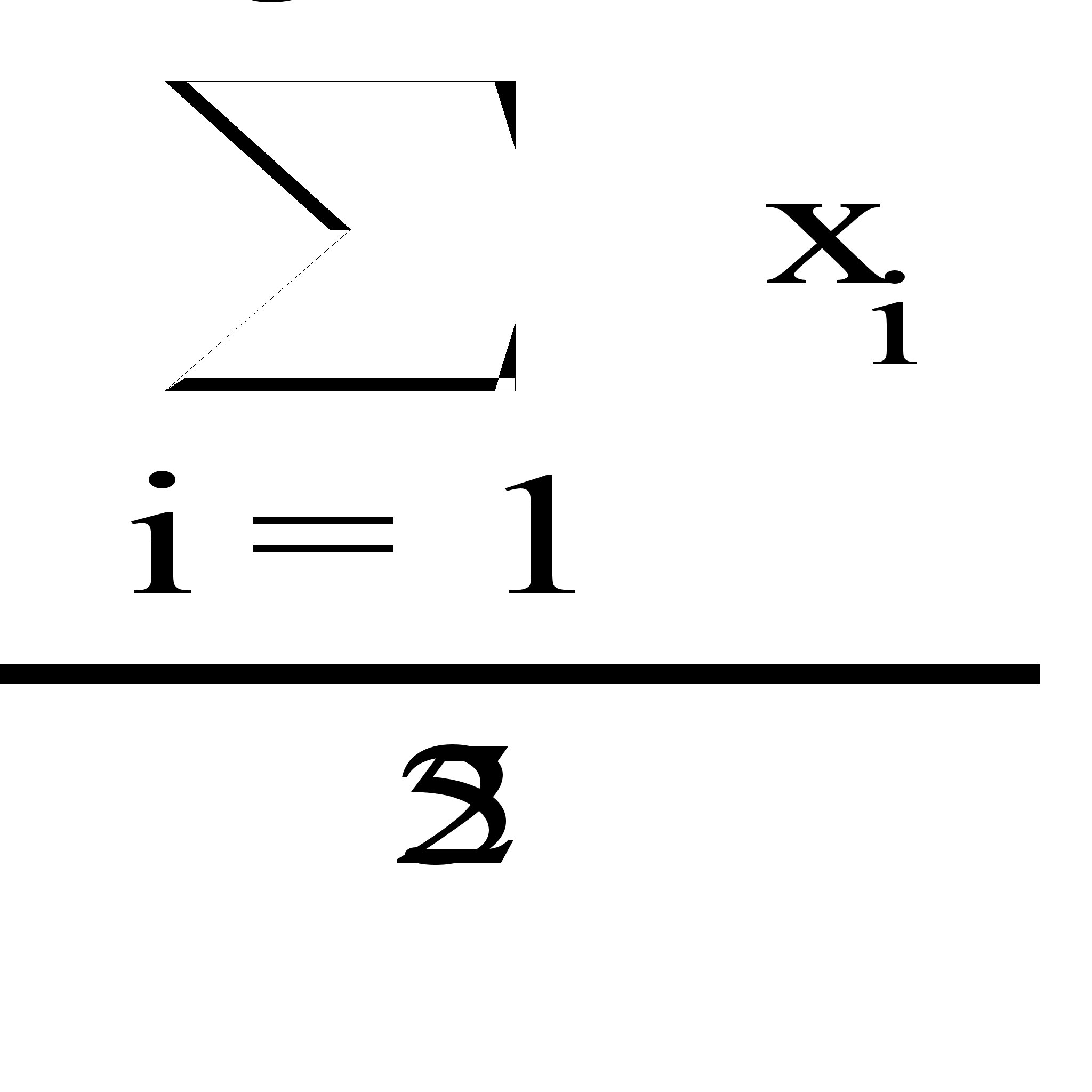
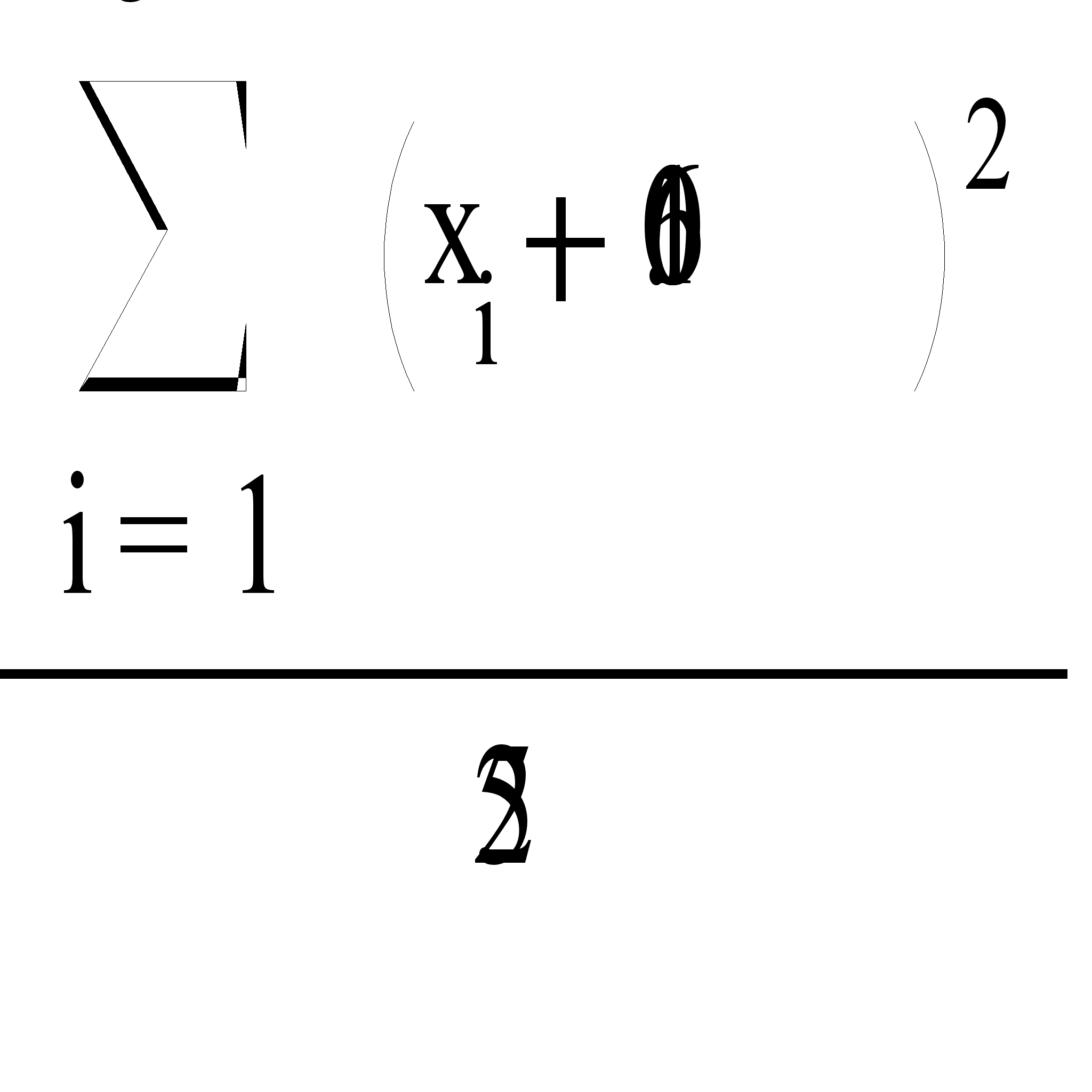
Найдем выборочную дисперсию по формуле

Получим 11 случайных чисел с законом распределения Стьюдента с 10 степенями свободы:

С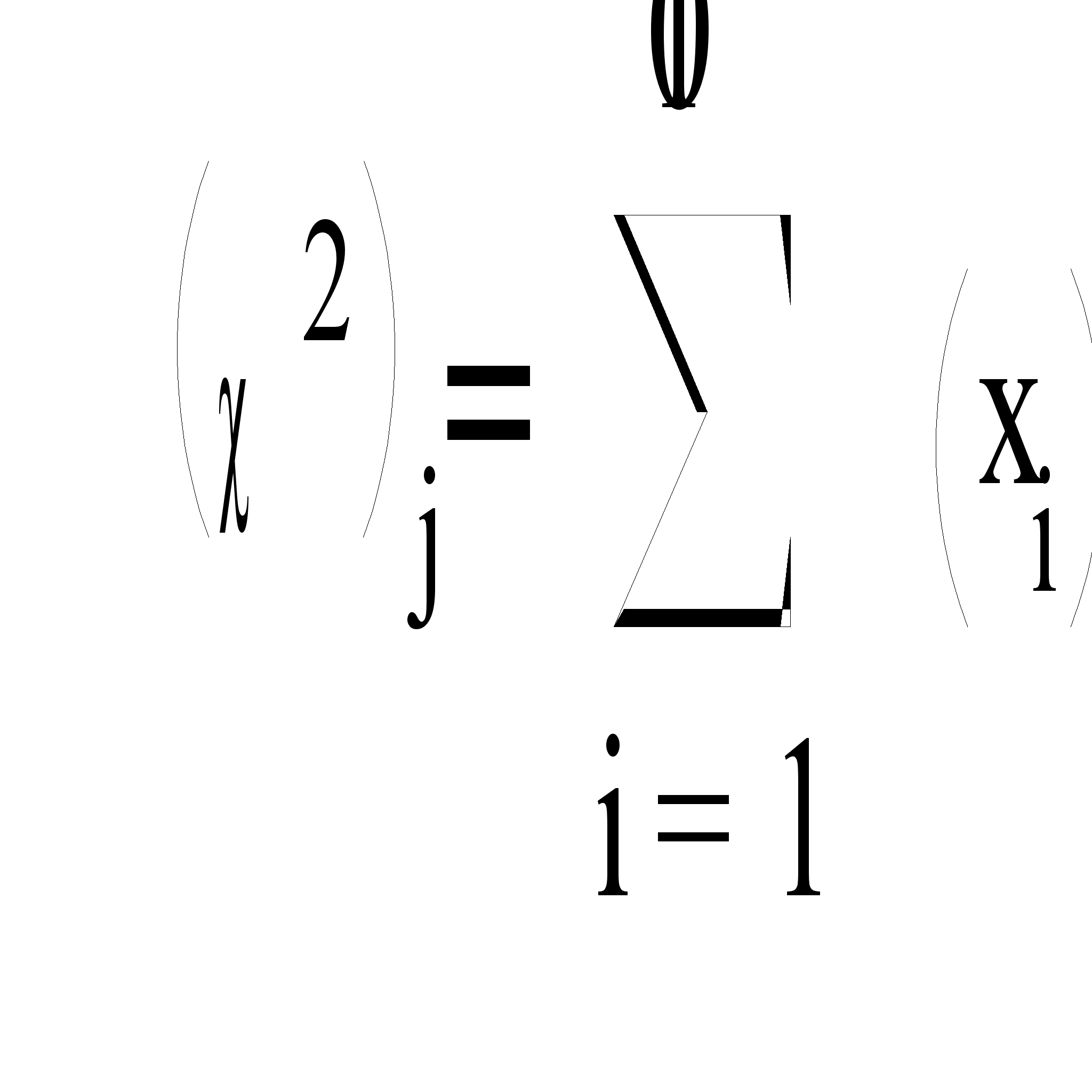
лучайные числа, распределенные по закону «хи квадрат» с 10 степенями свободы:

, где x_i – нормальные независимые случайные величины.

Случайные числа, распределенные по закону Стьюдента с 10 степенями свободы:

,
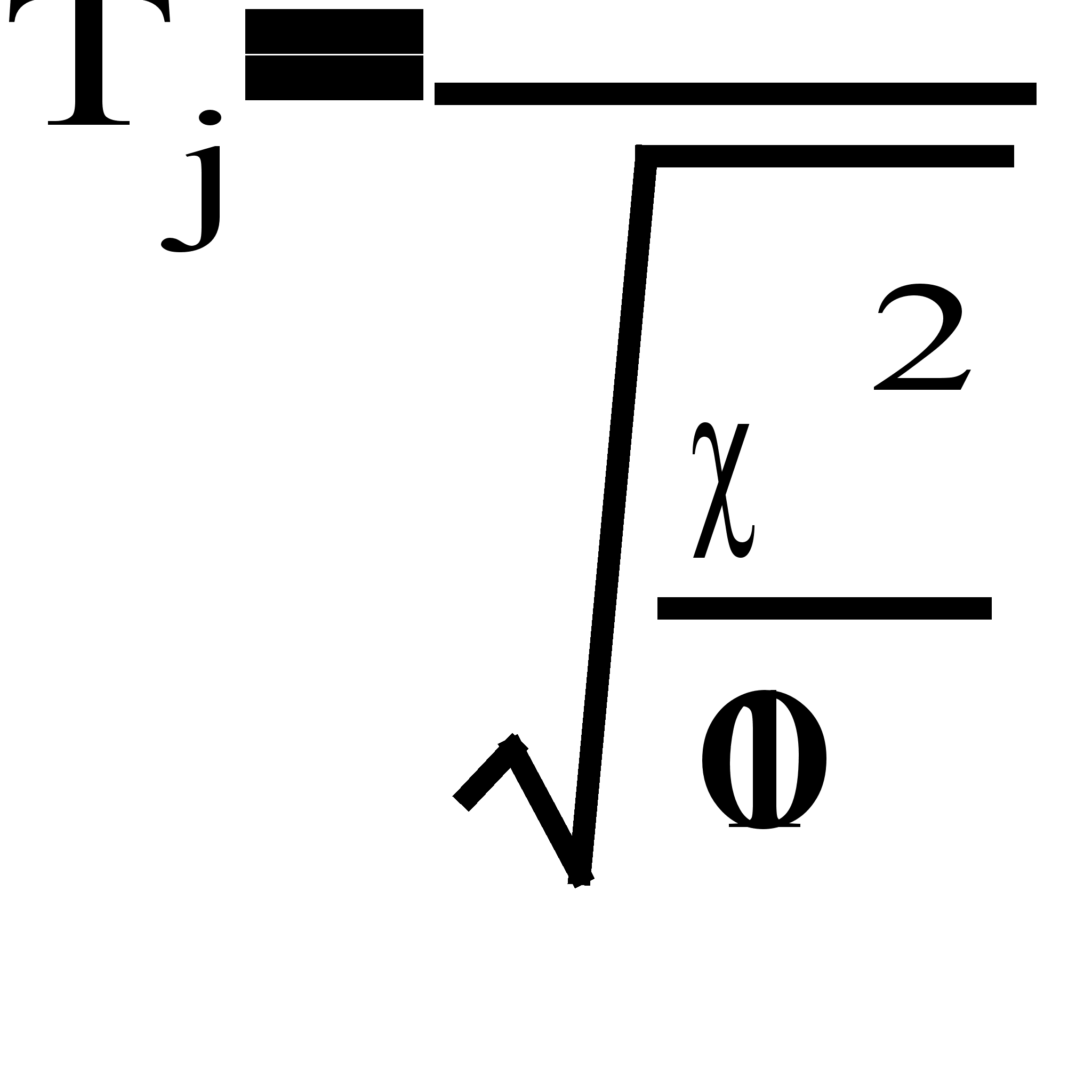
где x – нормальная случайная величина, а ² – независимая от x величина, которая распределена по закону «хи квадрат» с 10 степенями свободы.

Получены следующие числа:

0.58

2.496

0.06

0.932

1.547

0.418

1.658

1.51

0.171

0.821

1.728

Найдем выборочное среднее по формуле

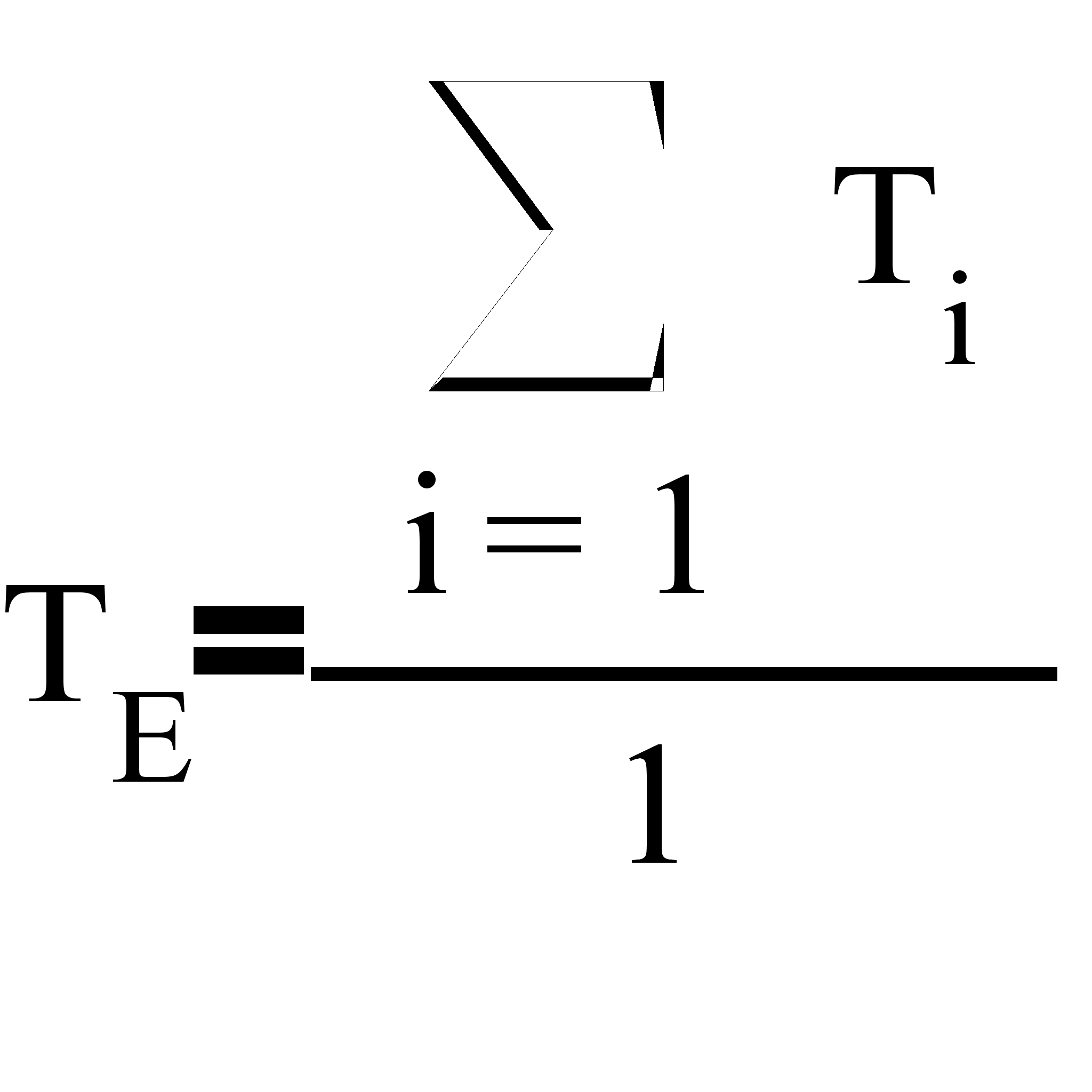
Найдем выборочную дисперсию по формуле

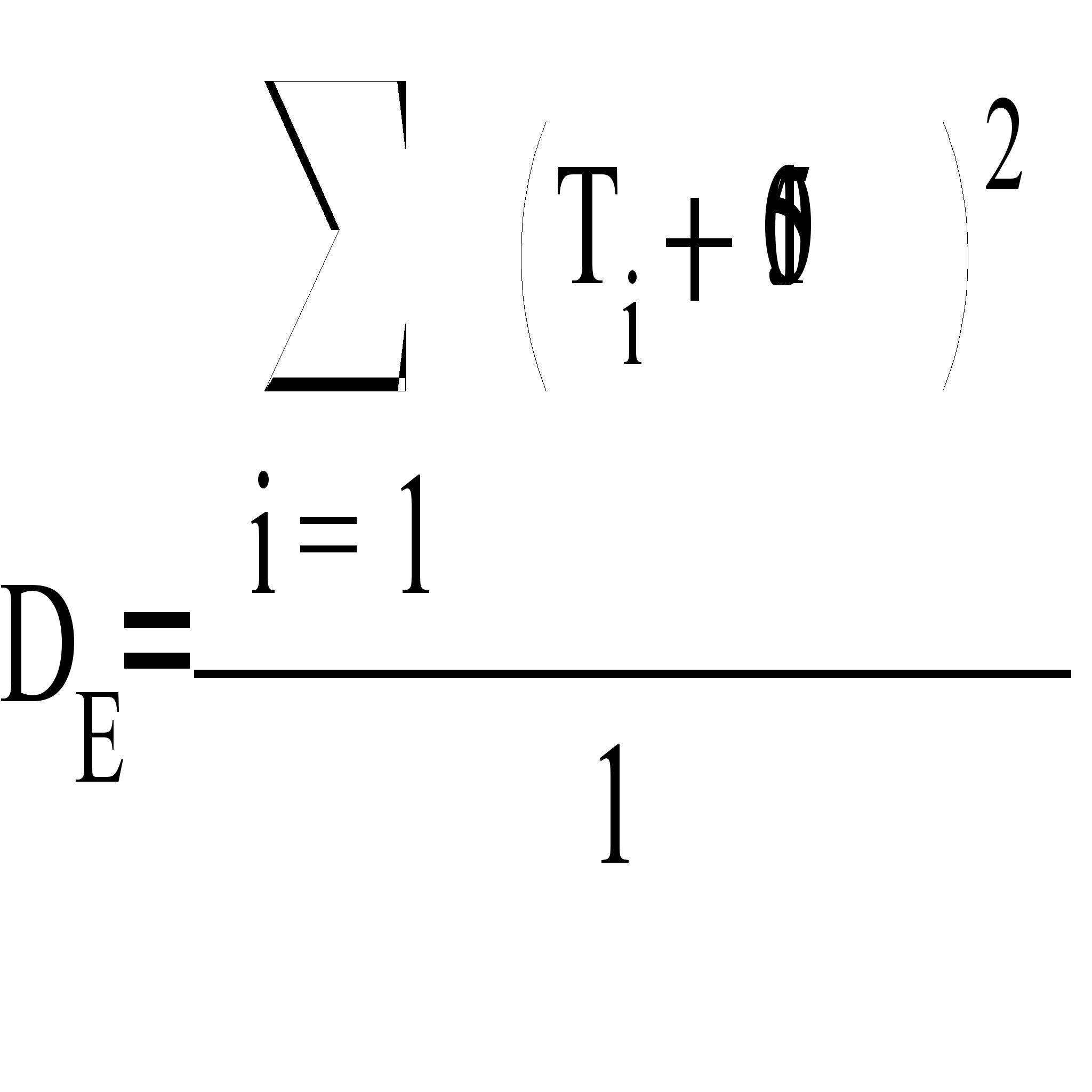
Задача 2.

Проверка статистической гипотезы:

1. получить 100 случайных чисел {x₁,…,x₁₀₀}, распределенных по показательному закону с параметром  = 1/6, найти такое наименьшее целое число N, что N  x_k для всех k = 1,…,100;

2. разделить отрезок [0, N] на 10 равных отрезков; получить группированную выборку {n₁,…,n₁₀}, где n_i – число чисел, попавших в iый интервал; построить гистограмму относительных частот; по группированной выборке найти оценку _В параметра ;

3. проверить с помощью критерия «хи квадрат» гипотезу о соответствии группированной выборки показательному распределению с параметром _В при уровне значимости 0.05.

Решение:

Получим 100 случайных чисел {x₁,…,x₁₀₀}, распределенных по показательному закону с параметром  = 1/6:

4,9713	3,2905	2,7849	4,1093	2,1764	9,9659	10,343	4,6924	13,966	14,161
0,4258	0,6683	8,8884	5,3392	2,7906	4,7696	3,0867	0,9414	2,8222	3,4177
10,148	3,5312	8,4915	3,0179	3,2209	4,2259	1,8006	2,8645	1,3051	3,3094
0,5557	1,9075	2,4227	6,9307	7,1085	13,322	0,9665	11,19	15,203	2,6685
3,6408	5,3646	4,5871	11,277	1,823	1,142	0,8126	7,2223	12,371	1,4527
2,9692	15,762	2,5493	13,533	8,8944	0,5005

Учебная работа № 1185. Теория вероятностей и математическая статистика