Учебная работа № 1155. Теория вероятностей
Вопрос 1
События и явления. Все события и явления реального мира разделяются на закономерные (детерминированные) и случайные (вероятностные).
Случайным событием называется такое событие, изменить или предсказать которое в процессе случайного явления невозможно. Случайное событие это результат (исход) конкретной единичной реализации случайного явления. Так, выпадение чисел 16 при бросании игральной кости случайное явление. Выпадение числа 6 в единичном испытании случайное событие. Если оно может задаваться, то это уже не игральная кость, а инструмент шулера. Типовое обозначение случайных событий крупными буквами алфавита (например, событие А выпадение 1 при бросании кости, событие В выпадение 2 и т.д.).
Классификация случайных событий. Событие называют достоверным (и обозначают индексом W), если оно однозначно и предсказуемо. Выпадение суммы чисел больше 1 и меньше 13 при бросании двух костей достоверное событие. Событие является невозможным (и обозначается индексом Æ), если в данном явлении оно полностью исключено. Сумма чисел, равная 1 или большая 12 при бросании двух костей события невозможные. События равновозможны, если шансы на их появление равны. Появление чисел 16 для игральной кости равновозможно.
Два события называются совместными, если появление одного из них не влияет и не исключает появление другого. Совместные события могут реализоваться одновременно, как, например, появление какоголибо числа на одной кости ни коим образом не влияет на появление чисел на другой кости. События несовместны, если в одном явлении или при одном испытании они не могут реализоваться одновременно и появление одного из них исключает появление другого (попадание в цель и промах несовместны).
1. Вероятность любого случайного события А является неотрицательной величиной, значение которой заключено в интервале от 0 до 1. 0 £ Р(А) £ 1.
2. Вероятность достоверного события равна 1. Р( W) = 1.
В общем случае событие W представляет собой сумму полной группы возможных элементарных событий данного случайного явления: W=![]() wi . Следовательно, вероятность реализации хотя бы одного случайного события из полной группы возможных событий также равна 1, т.е. является событием достоверным.
wi . Следовательно, вероятность реализации хотя бы одного случайного события из полной группы возможных событий также равна 1, т.е. является событием достоверным.
Сумма противоположных событий тоже составляет полную группу событий и соответственно вероятность суммы противоположных событий равна 1:P(A+![]() ) = 1.
) = 1.
Примером может служить бросание горсти монет. Орел или решка для каждой монеты – противоположные события. Сумма событий для горсти в целом равна 1 независимо от соотношения выпавших орлов и решек.
3. Вероятность невозможного события равна 0. Р( Æ) = 0.
|
Рис. 8.2.3. |
Пусть Ф пустое пространство (не содержащее событий). Тогда W+Ф = W и пространство W не содержит событий, общих с пространством Ф (рис. 8.2.3). Отсюда следует, что Р( W+Ф) = Р( W) + Р(Ф) = Р( W), что выполняется при Р(Ф) = 0. Другими словами, если одно из событий обязательно должно происходить, то вероятность отсутствия событий должна быть равна нулю. Но при этом W является достоверным событием, а Ф = Æ (невозможное событие) и соответственно Р( Æ) = 0.
Вопрос 2
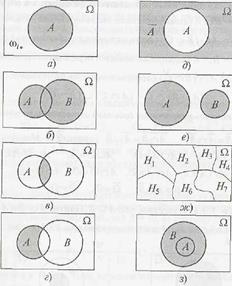 Диаграмма ВьеннаЭйлера
Диаграмма ВьеннаЭйлера
А) событие A
Б) Сложение – событие, кот состоит в том, что происходит хотя бы одно из событий A или B
В) произведение событий А и B одновременно
Г) Дополнение – событие принадлежит к А, но не принадлежит к B
Д) противоположное событию A событие В
Е) Несовместимые события – если они не могут произойти одноременно
Ж) События образуют полную группу, если хотя бы одно из них обязательно происходит в результате испытания
З) А влечет за собой В
Вопрос 3
Классическая формула вероятности
Если множество элементарных событий Ω={ ω 1, ω 2,…ω N},конечно и все элементарные события равновозможны, то такая вероятностная схема носит название классической . В этом случае вероятность Р{А} наступления события А, состоящего из М элементарных событий, входящих в Ω, определяется как отношение числа М элементарных событий, благоприятствующих наступлению события А, к общему числу N элементарных событий. Эта формула носит название классической формулы вероятности: Р{А}= M/ N.
В частности, согласно классической формуле вероятности:
Р{ ω i }=1/ N ( i=1,2,… , N)
Р{ Ω}= N/ N =1
P{ Æ}=0/ N =0
Комбинаторика, 1) то же, что математический комбинаторный анализ. 2) Раздел элементарной математики, связанный с изучением количества комбинаций, подчинённых тем или иным условиям, которые можно составить из заданного конечного множества объектов (безразлично, какой природы; это могут быть буквы, цифры, какиелибо предметы и т.п.). Число размещений . Пусть имеется n различных предметов. Сколькими способами можно выбрать из них т предметов (учитывая порядок, в котором выбираются предметы)? Число способов равно An m = ![]() ? An m называют числом размещений из n элементов по m. Число сочетаний. Пусть имеется n различных предметов. Сколькими способами можно выбрать из них т предметов (безразлично, в каком порядке выбираются предметы)? Число способов такого выбора равно Cn m =
? An m называют числом размещений из n элементов по m. Число сочетаний. Пусть имеется n различных предметов. Сколькими способами можно выбрать из них т предметов (безразлично, в каком порядке выбираются предметы)? Число способов такого выбора равно Cn m = ![]() Cn m называют числом сочетаний из n элементов по m. Числа Cn m получаются как коэффициенты разложения nй степени двучлена: ( a+ b) n = Cn 0 an + Cn 1 an 1 b + Cn 2 an 2 b2 ? +… + Cn n1 abn1 + Cn n bn , и поэтому они называются также биномиальными коэффициентами. Основные соотношения для биномиальных коэффициентов: Cn m =Cn nm , Cn m? + Cn m+1 = Cn+1 m+1 , Cn 0 + Cn 1 + Cn 2 +…+ Cn n1 + Cn n =2n , ? Cn 0 Cn 1 + Cn 2 …+ (1) n Cn n = 0. Числа An m , Pm и Cn m связаны соотношением: An m =Pm Cn m . Рассматриваются также размещения с повторением (т. е. всевозможные наборы из m предметов n различных видов, порядок в наборе существен) и сочетания с повторением (то же, но порядок в наборе не существен). Число размещений с повторением даётся формулой nm , число сочетаний с повторением формулой Cm n +m1 .
Cn m называют числом сочетаний из n элементов по m. Числа Cn m получаются как коэффициенты разложения nй степени двучлена: ( a+ b) n = Cn 0 an + Cn 1 an 1 b + Cn 2 an 2 b2 ? +… + Cn n1 abn1 + Cn n bn , и поэтому они называются также биномиальными коэффициентами. Основные соотношения для биномиальных коэффициентов: Cn m =Cn nm , Cn m? + Cn m+1 = Cn+1 m+1 , Cn 0 + Cn 1 + Cn 2 +…+ Cn n1 + Cn n =2n , ? Cn 0 Cn 1 + Cn 2 …+ (1) n Cn n = 0. Числа An m , Pm и Cn m связаны соотношением: An m =Pm Cn m . Рассматриваются также размещения с повторением (т. е. всевозможные наборы из m предметов n различных видов, порядок в наборе существен) и сочетания с повторением (то же, но порядок в наборе не существен). Число размещений с повторением даётся формулой nm , число сочетаний с повторением формулой Cm n +m1 .
Вопрос 4
При аксиоматическом построении вероятностей в каждом конкретном пространстве элементарных событий W выделяется sполе событий Sдля каждого события A Î Sзадается вероятность P{ A} – числовая функция, определенная на sполе событий Sи удовлетворяющая следующим аксиомам.
Аксиома неотрицательности вероятности для всех A Î S: P{ A} ³ 0.
Аксиома нормированности вероятности: P{ W}=1.
Аксиома адаптивности вероятности: для всех A, B Î S,таких, что A Ç B ¹ Æ: P{ A È B}= P{ A} + P{ B}
Каждая определенная теоретиковероятностная схема задается тройкой { W, S, P}, где W конкретное пространство элементарных событий, S sполе событий, выделенное на W, З – вероятность заданная на sполе S. Тройка { W, S, P} называется вероятностным пространством
Пусть проводится конечное число nпоследовательных испытаний, в каждом из которых некоторое событие А может либо наступить (такую ситуацию назовём успехом),либо не наступить (такую ситуацию назовём неудаxей),причём эти испытания удовлетворяют следующим условиям:
1)каждое испытание случайно относительно события А, т.е. до проведения испытания нельзя сказать появится А или нет;
2)испытания проводятся в одинаковых с вероятностной точки зрения условиях, т.е. вероятность успеха в каждом отдельно взятом испытании равна р и не меняется от испытания к испытанию;
3)испытания независимы, т.е. исход любого из них никак не влияет на исходы других испытаний.
Такая последовательность испытаний называется схемой Бернулли или биноминальной схемой, а сами испытания испытаниями Бернулли.
Фла Бернулли: Рm n = Cm n * pm * qn m = Cm n * pm * (1p)n m
C

 (3 оценок, среднее: 4,67 из 5)
(3 оценок, среднее: 4,67 из 5)