Учебная работа № 1070. Дискретная математика

Учебная работа № 1070. Дискретная математика

Стр. 11

Задание № 5

В 92процессорном ЭВС 19 микропроцессоров обрабатываюттекстовую информацию, 17 – графическую, 11 символьную, 12 микропроцессоров одновременно обрабатывают графическую и текстовую, 7 текстовую и символьную, 5 графическую и символьную, а часть микропроцессоров одновременно обрабатывают графическую, текстовую и символьную информацию.

Сколько микропроцессоров являются универсальными, если при решении задачи не задействованы 67 микропроцессоров.

Задание № 6.

Пусть Х=(АВ)С и Y = A(BC) Доказать, что Х Y и YX = АС

Задание № 7.

Определить число всевозможных слов длины 5, если А = {X,Y} алфавит.

Задание № 7.1

Определить число всевозможных слов длины 4, если А = {X,Y,Z,T} алфавит.

Задание № 8.

Указать области определения и значения для соответствия «Больше», если А = {2,4,6} ;R={1,4,6,7}

Задание № 9.

Из них 19 не сдали математику, 17 физику, 11 программирование, 12 студентов не сдали математику и физику, 7 математику и программирование, 5 физику и программирование; 237 сдалиматематику, физику, программирование. Сколько студентов безуспешно (т.е. не сдавшие 3й экзамена)

закончили сессию ?

Задание № 10.

Доказать справедливость следующих выражений: АÇ(В\С); (А В)\С, (aÈb)\c=(a\С)È(b\c)

Стр. 1(23)

Задание № 11.

Сколько соответствий можно установить меж ду элементами множеств A={k, l,m, n} и В= {В1, В2. ВЗ} Какие из этих соответствий являются отображениями ? К каким типам относятся приведенные соответствия ?

Задание № 12.

Для общего собрания старшекурсников МИЭМ (1240 студентов) все 40 старост были оповещены по телефону, с тем, чтобы они оповестили студентов своих групп. Каждый из старост позвонил студентам и попросил их позвонить другим студентам. При условии « равенство» определить их. если ни одно лицо не оповещается дважд ы.

Задание № 13.

К каким видам относятся следующие множеств а : А множество всех простых чисел натурального рядаN ; В множество деревье в на луне ; С множество всех решений уравнения 2х 3= 0?

З адани е № 14.

Для написа ни я цифр почтового индекса исп ольз уют множество из дев яти элементов , которые на рисун ке обозначены буквами. Запишите множества Ак (к = 0,9) элементов каждой из десяти цифр. Имеются ли среди этих множеств непересекающиеся ?

Задание № 15.

В химическом продукте могут оказаться примеси четырех видов a. b, c,d. Приняв в качестве исходного множества М = { a, b, c. d}. Образуйте множество всех его подмножеств В (М). Дайте содержательную интерпретацию этого множества и его элементов. Каким ситуациям соответствуют, в частности, несобственные подмножества ?

З адание № 16.

Доказать, что для любых множеств А и В справедливо соотношение : О А В А В

З адание № 17.

Определить число всех n последовательностей из нулей и единиц (т.е. двоичных кодов длины n).

З адание № 18.

Сколько студентов из группы в 30 человек изучают по свободному учебному плану три дисциплины, если известно; 19 студентов изучают ТАР, 17 конструкрованне ЭВС. 11 технологию ЭВС. 12 ТАР и КЭВС, 7 ТАР и ТЭВС, 5 КЭВС и ТЭВС , в пять студентов обучается по типовому плану.

Задание № 19.

Доказать, что, выбрав одно слово из словаря, содержащего 90000 слов на 915 страницах, его можно определить пу тем 17 вопросов, на которые отвечают лишь « да« или « нет».

Задание № 20.

Указать область определения и значения для соответствия «равенство« ,

если А 4, 5 ; В 2, 6, 8, 9

Задание № 21.

определить число всех слов длины 4, если алфавит: А = X, Y.

Стр. 21

Задача № 37.

Сколько конструктивов ЗВС эксплуатируемой в соответствующих условиях не резонирует от дестабилизирующих механических факторов частоты f 1и f2, если известно: число конструктивов 67, из н их 47 резонируют при f1; 35 резонируют при f2; 20 резонируют при f3, 23 резонируют при f1 b f2; 12 резонируют при f1 и f3; 5 резонируют при всех частотах объекта установки, то есть f1, f2 b f3.

Стр. 31

Задачи по дискретн ой мате матике. Ра здел: Тео рия м ноже ств.

4.

Доказать, что система счисл ения с основанием « 3« являются наиболее экономичными.

5.

Ско лько покрывающи х д еревьев можн о образ овать н а мно жестве верши н, если си мвол каждого дерева и меет дл ину 21? Результат обосноват ь и док азать.

6.

Какие и з ниж еприведенных неверны и поче му?

x{ 2, а, х}; 3 { 1,{ 2, 3} ,4}; x { l,co s x}; (x, y ) { a, {x,y} ,b}.

7.

Образуйте мн ожество праздничных д ней пе рвых трех месяце в 1996 года. Пересекается ли это мно жество с мн ожеством воск ресных дне й тех же м есяце в 1996 года? Запи шит е элемент ы п ересечени я эти х м ножест в.

12.

Для 2 множеств X= x1, x2, x3, x4, x5, x6 и Y = yl, y 2, y3 , y4 определено бинар ное отношение A=( x1,x2)(x2 ,y 1)(x2,y 1)(x 4,y 2), (x4,y 3)( x5,y 1)( x5,y 3) Для данного отношения А:

· записать область определения и обл асть знач.

· определит ь симметрию отношении А.

17.

Рав ны ли между собой множест ва А и В (если нет , то почем у?)

А = { 1 ,(2,5),6} , В= { 1,2,5,6};

a) A={2 ,4,5}, В={ 5,2,4}; А={1,2,4,2}, B={1,2,4};

b) A={2,4,5 },B ={2,4,3}; A={ 1,{2, 5}, 6},B={ 1,{ 5, 2}, 6}; A={ 1,{2,7},8}, B={1, (2, 7) ,8}.

18.

B каких отношениях находятся между собой множества А, В, С?

а) А={1,3}; В={х: х нечетное число}; С={х: х4х+3=0};

б) А={2,5}; В={х; х целое число }; С={х: х 7х +10=0}.

19.

К каким видам относятся следующие множества:

а) А множества ИС в АЛУ; В множества квадратньгх целых чисел. С={х: 2хЗ=О}; Д={х: у дерево, растущее на Луне}

б) А множество МП в УУ; В .множество простых чисел; С={у: 3у7=0}; Д={z: z слон без хобота}?

20.

Сколько различных семибуквенных слов можно составить из букв русского языка, не обращая внимания на их семантику?

21.

Представьте бинарное отношение, задание графом

как множество упорядоченных пар и запишите его матрицу. Какими свойствами характеризуется данное отношение?

стр. 41

1.

Покажите, что для любого рефлексивного отношения А отношения А È А¹ и АÇА» являются толерантностями.

2.

В общем случае объединение отношений эквивалентности А и В не явля­ется эквивалентностью. Приведите примеры, подтверждающие это положе­ние.

3

Найти число способов распределения студенческой группы из 23 человек на бригады по 3 и 5 человек.

4.

Покажите, что композиция А*В антирефлексивных отношений А и В то­гда и только тогда антирефлексивна, когда АÇВ¹ =0 .

5.

Докажите тождество:

8.

Сколько различных фигур можно изобразить с всевозможных комбинаций из элементов а, б, в,…, и почтового индекса если в каждой комбинации может присутствовать от 0 до 9 элементов

9.

Определить число всевозможных слов длины 5, если А=Х1….,Х5алфавит.

10.

Какие из приведенных ниже выражений неверны и почему:

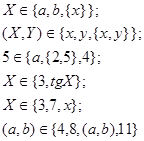
11.

Доказать, что на множестве всех групп 2го курса факультета АВТ нужно 3 вопроса студенту, па которые он отвечает «Да» или «Нет’, можно опреде­лить шифр его группы.

13.

Записать в виде теор. множественных соотношений следующие утвержде­ния: среди деталей первого узла имеются все пластмассовые детали одинаковый детали, входящие в оба узла могут быть только пластмассовы­ми во втором узле нет пластмассовых деталей При записи учесть, что M1 иМ2, соответственно, множества деталей 1го и 2го узла, А – множество пластмассовых деталей.

16.

Связаны лн множества А и В отношением включения (если ДА, то ука­жите какое из них является подмножеством другого):

a) A={a.b.d}, B={b,d.a,c}, А={a,c,d,e},В={а,с,е},

b) А={c,d,e},В={а,с}, A={a,(c,d),e}, B={a.e,(c, d),k}.

19.

Представьте в виде композиции функций функцию

20.

Покажите, что следующая функция имеет обратные ей функции:

Найти области определения и значения обратной функции и начертить их графики.

21.

Исходя из определения дизъюнктивной суммы, покажите ее свойства (коммутативность, ассоциативность, дистрибутивность пересечения отно­сительно симметрии разности).

22.

Доказать справедливость:

/конец стр. 42/

/стр. 71/

Вопросы по разделу » Основы теории множеств».

1.

Сколько различны х трехбуквенных слоев можно составить из букв русского алфавита, не обращая внимания на их смысл .

2.

Сколько покрывающих деревьев можно образовать, если символ каждого дерева имеет длину 15.

3.

Доказать, что для конеч ного мнва из n элементов , множество всех его подмножеств содержит 2ⁿ элементов.

4. /вставить рисунок/

Сколько различных фигур можно изобразить с помощью всевозмо жны х комбинаций и з элементов « а, б,.., и почт ового индекса, если в каждой комбинации может присутствовать от 0 до 9 элементов.

5.

Покажите, что для любого множества М справедливы соотнош ения:

Æ, М ÅÆ = М.

6.

Покажите, что для любы х множеств А и В справедливо соотношение

7.

Покажите, что из соотношения следует СÌ A и C Ì B.

8

Запишите множество упорядоченных пар ( x,y), выражающих отноше­ние « x делитель y « на множестве целых чисел от 2 до 10 включительно? Является ли это отношение функцией? Обладает ли оно свойством транзитивности?

9.

Пусть x Î X и y Î Y и A – отношение между элементами множеств X и Y, т. е.: xAy. Укажите, в каких случаях A можно рассмат­ривать как функцию:

а) X множество студентов, Y множество учебных дисциплин xAy « x изучает y «.

б)x множество студентов, y рост в единицах длины, xAy «x и меет рост y«;

в) x множе ство интегральных схем печатного узла y множество. печатных узлов, xAy «x входит в y».

Учебная работа № 1070. Дискретная математика