Учебная работа № 2092. Движение в центральном симметричном поле
Реферат
На тему «Движение в центральном симметричном поле»
Студента I –го курса гр. 107
Шлыковича Сергея
Минск 2001
Немного теории.
Центральным называют такое силовое поле, в котором потенциальная энергия частицы является функцией только от расстояния r до определенной точки центра поля: U= U( r). Сила, действующая на частицу в таком поле, тоже зависит лишь от расстояния r и направлена в каждой точке пространства вдоль радиуса, проведенного в эту точку из центра поля.
Хотя частица, движущаяся в таком поле, и не представляет собой замкнутую систему, тем не менее для нее выполняется закон сохранения момента импульса, если определять момент по отношению к центру поля. Действительно, поскольку направление действующей на частицу силы проходит через центр поля, то равно нулю плечо силы относительно этой точки, а потому равен нулю и момент силы. Согласно уравнению ![]() отсюда следует, что L = const .
отсюда следует, что L = const .
(где L – вектор момента импульса, а K момент силы K = [rF ]. Уравнение ![]()
![]()
![]()
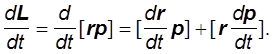
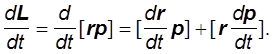
Так как ![]()
![]()
![]()
![]()


Поскольку момент L = m [rv ] перпендикулярен направлению радиусавектора r , то из постоянства направления L следует, что при движении частицы ее радиусвектор должен оставаться все время в одной плоскости плоскости, перпендикулярной направлению L . Таким образом, в центральном поле частицы движутся по плоским орбитам орбитам, лежащим в плоскостях, проходящих через центр поля.
Данное уравнение можно записать в виде:
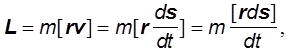
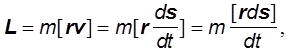
  |
где ds вектор перемещения материальной точки за время dt. Величина векторного прои зв едешь двух векторов геометрически представляет собой лощадь построенного на них параллелограмма. Площадь же параллелограмма, построенного на векторах ds и r , есть удвоенная площадь бесконечно узкого сектора OAA’ , описанного радиусомвектором дви жущейся точки за время dt . Обозначив эту площадь через dS, можно записать велич

 (6 оценок, среднее: 4,67 из 5)
(6 оценок, среднее: 4,67 из 5)