Учебная работа № 2051. Бернулли

Учебная работа № 2051. Бернулли

В то время как большинство западноевропейских стран были заняты внутренними феодальными междоусобицами и внешними войнами, Нидерланды уже прошли немалый путь капиталистического развития. Иностранцев поражало в Нидерландах цветущее состояние городов, отсутствие феодальных форм отношений между различными слоями населения, высокий уровень жизни, расцвет науки и культуры. Эта сравнительно небольшая страна давала казне львиную долю доходов. Годовой сбор налогов, например, достигал двух миллионов флоринов, в то время как вся Испания давала один миллион. Карл V называл Нидерланды жемчужиной своей короны.

Протестантство появилось в Нидерландах вскоре после известного выступления Лютера 1517 г., направленною против продажи индульгенций. Борьба против испанского ига переплелась с борьбой за свободу вероисповедания. Народное движение приняло религиозную окраску и разливалось шире и шире по стране.

В 1550 г. Карл V издал указ против еретиков, поставивший фактически всех протестантов вне закона и объявивший неограниченный террор на всей территории Нидерландов.

Пришел конец элементарной законности. С безграничным цинизмом без суда уничтожались целые семьи, и даже роды. Вместе с казнями состоятельных граждан отторгалось принадлежавшее им имущество, изымались деньги и ценности. Началась эмиграция. Она достигла таких размеров, что многие местечки обезлюдели, а в городах численность населения заметно уменьшилась.

Купеческая протестантская семья Бернулли жила в Антверпене. Свой род она вела из Фландрии, где Бернулли, в XV в. носившие еще фамилию Бернуйла (Bernuilla), не избегали и военных дел. Семья держалась насиженного места, пока можно было рассчитывать на то, что все както устроится. Надежды связывались с успехами освободительного движения: несмотря на зверства Альбы, северные провинции Нидерландов, объединенные вокруг Вильгельма Оранского, вынудили Филиппа признать их право на самоопределение. По договору 1579 г. семь северных провинций, образовавших ядро будущей Голландии, освобождались от испанского владычества. Однако остальные провинции—и город Антверпен, в том числе — оставались под испанской короной.

Тем самым все надежды рушились. Под угрозой физического уничтожения приходилось покидать родной город. Большинство эмигрантов направлялось в прирейнские провинции Германии, потому что еще при жизни Карла V Германия добилась свободы вероисповедания (Аугсбургский мир 1555 г.). Казалось, волнения там улеглись и можно будет отдохнуть от десятилетий террора. Семья Бернулли решает ехать во ФранкфуртнаМайне. Реформация в этом городе прошла еще в 1533 г., господствующая религия—протестантская. Выбор кажется удачным. В 1582 г. семья трогается в путь. Нелегко было порывать с родными местами. Глава семьи, Якоб Бернулли, скончался во Франкфурте в следующем же году.

Расчеты эмигрантов на то, что удастся обосноваться на новом месте, не оправдались: и в Германии вражда между католиками и протестантами не угасала. С начала XVII в. атмосфера непрерывно сгущалась; в 1618 г. началась Тридцатилетняя война, принесшая с собой неслыханные бедствия и расстройство хозяйственных связей. Решено было искать спокойного пристанища. Выбор остановился на Швейцарии, а именно на Базеле. Положение в Швейцарии казалось относительно спокойным: реформация там утвердилась в 20е годы XVI столетия, религиозные волнения за протекшие сто лет улеглись. В 1622 г. другой Якоб, внук первого Якоба, переехал в Базель и принял гражданство Базельской республики. На этот раз эмиграция завершается удачно. Сын Якоба Николай уже видное лицо в городе, пользующийся уважением купец, глава семьи, состоящей из одиннадцати детей. Среди его детей и находятся те, с кого начинается династия выдающихся математиков.

Чем вызвано переселение Бернулли именно в Базель, трудно сказать. Единственно, что можно утверждать с полной уверенностью, это то, что наличие в городе университета не играло в выборе никакой роли: семья Бернулли из поколения в поколение старалась отвлечь свою молодежь от науки и обратить ее дарования на коммерческую деятельность или адвокатуру. К счастью, молодежь сама выбирала свои пути, не очень считаясь с желаниями старших.

Среди Бернулли некоторые имена повторяются из поколения в поколение, поэтому их различают, как королей, присоединив к имени соответствующую цифру. Вот родословная Бернулли:

Якоб (15981634). Уроженец ФранкфуртанаМайно. В 1622 г. переехал на постоянное жительство в Базель.

Николай (16231708). Сын Якоба. Уроженец Базеля. Торговец аптекарскими товарами и лекарственными травами. Член Большого совета Базеля и член суда. Имел 11 детей.

Якоб I (16541705). Сын Николая. По образованию богослов. С 1687 г. профессор математики Базельского университета. Учениками Якоба I были: его младший брат Иоганн I, племянник Николай I, член Петербургской академии наук, механик и математик Я. Герман, отец великого Л. Эйлера — Пауль Эйлер.

Николай (16621716). Брат Якоба I. Живописец. Член суда.

Иоганн I (16671748). Брат Якоба I. Десятый ребенок в семье Николая. По образованию врач. С 1695 г. профессор математики Гронингенского университета (Голландия). С 1705 г. профессор математики Базельского университета. Почетный член Петербургской академии наук.

Жером (16691760). Брат Иоганна I. Торговец аптекарскими товарами.

Николай. Единственный сын Якоба I, имевшего еще дочь. Вопреки желанию отца, уклонился от научной карьеры и стал живописцем. По словам современников, весьма посредственным.

Николай I (16871759). Сын Николая. По образованию юрист. Профессор математики в Падуе, профессор логики и права в Базеле.

Николай II (16951726), сын Иоганна I. По образованию юрист. Профессор права в Берне, профессор математики в Петербурге.

Даниил I (17001782). Уроженец Гронингена. Сын Иоганна I. По образованию врач. В 17251733 гг. работал на кафедрах физиологии и механики в Петербургской академии наук. С 1733 г. профессор по кафедре физиологии, с 1750 г. профессор по кафедре механики в Базеле. Почетный член Петербургской академии наук.

Иоганн II (17101790), Сын Иоганна I. По образованию юрист. Профессор элоквенции (красноречия), профессор математики в Базеле.

Иоганн III (17441807). Старший сын Иоганна II. По образованию юрист. Астроном Берлинской академии наук, там же директор математического класса.

Даниил II (17511834). Второй сын Иоганна II. По образованию врач, профессор красноречия в Базеле.

Якоб II (17591789). Третий сын Иоганна II. По образованию юрист. Математик Петербургской академии наук. Утонул в Неве.

Кристоф (17821863). Сын Даниила II. Профессор технологии в Базеле.

ИоганнГустав (18111863). Сын Кристофа. Профессор технологии в Базеле.

Представители рода Бернулли живут в Базеле и в настоящее время.

Якоб (15981634)

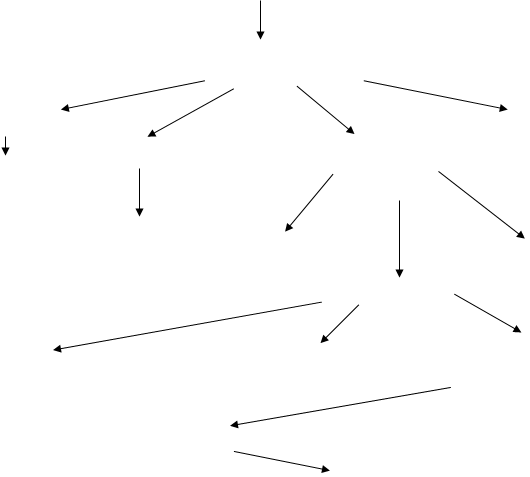
Николай (16231708)

Якоб I (16541705) Жером(16691760)

Николай(16621716) Иоганн I (16671748)

Николай

Николай I (16871759)

Николай II (16951726) Даниил I (17001782)

Иоганн II (17101790)

Якоб II (17591789) Иоганн III (17441807) Даниил II(17511834)

Кристоф(17821863)

ИоганнГустав(18111863)

Якоб I. Родился 27 декабря 1654 г. По желанию отца готовился к званию протестантского священника. Окончил Базельский университет, где изучал философию, богословие и языки. Владел немецким, французским, английским, итальянским, латинским и греческим языками. Испытывая непреодолимое влечение к математике, изучал ее тайком от отца. В 1671 г. получил степень магистра философии. С большим успехом читал проповеди на немецком и французском языках. В то же время продолжал пополнять свои знания по математике без учителя, почти без учебников.

В октябре 1686 г. оказывается вакантной должность профессора математики в Базельском университете. Успехи Якоба в математике хорошо известны, и Сенат университета единодушно выдвинул на вакантную должность Якоба Бернулли. Вступление в должность состоялось 15 февраля 1687 г. Вряд ли присутствовавшие при этом скромном акте представляли, что они являются свидетелями начала беспримерного в истории математики события: отныне кафедру будут занимать Бернулли на протяжении ста лет. Члены же этой семьи будут профессорами родного университета в течение четверти тысячелетия, вплоть до второй половины XX в.

В том же году Якоб Бернулли прочитал в «Асtа Eruditirum» за 1684 г. «Новый метод» Лейбница и, обнаружив трудные места, письменно обратился к Лейбницу за разъяснением. Лейбниц, находившийся в длительной служебной поездке, получил письмо только через три года, когда надобность в консультации отпала: Якоб совместно Иоганном овладели дифференциальным и интегральным исчислениями настолько, что вскоре смогли приступить систематическому развитию метода. Образовавшийся триумвират — Лейбниц, Якоб и Иоганн Бернулли — менее чем за двадцать лет чрезвычайно обогатил анализ бесконечно малых.

С 1677 г. Я. Бернулли стал вести записные книжки, куда вносил различного рода заметки научного содержания. Первые записи посвящены теологии, сделаны под влиянием распространенного в то время в Базеле сборника спорных теологических вопросов.

Основное место в записных книжках занимает решение задач. Уже по ранним записям можно судить о проявленном Я. Бернулли интересе к прикладной математике. Математические заметки показывают, как постепенно Я. Бернулли овладевал методами Валлиса, Декарта, инфинитезимальными методами, как развивал и совершенствовал их. Решенные им задачи служили отправными пунктами для дальнейших более глубоких исследований.

В январе 1684 г. Я. Бернулли провел в Базельском университете открытый диспут, на котором защищал 100 тезисов, из них 34 логических, 18 диалектических и 48 смешанных. Некоторые тезисы крайне любопытны. Вот примеры:

«78. Иногда существует несколько кратчайших путей из точки в точку.

83. .Среди изопериметрических фигур одна может быть в бесконечное число раз больше другой.

85. Не в каждом треугольнике сумма внутренних углов равна двум прямым.

89. Квадратура круга еще не найдена, но не потому, что между искривленным и прямолинейным нет никакой связи; в действительности кривую можно спрямить, а криволинейную фигуру квадрировать»

В мае 1690 г. Я. Бернулли опубликовал в «Асtа Eruditirum» первую работу, связанную с исчислением бесконечно малых. В ней он дал решение поставленной Лейбницем в 1687 г. задачи о парацентрической изохроне. Необходимо было найти кривую, по которой материальная точка опускалась бы в равные промежутки времени на равные высоты. Я. Бернулли вывел дифференциальное уравнение кривой и проинтегрировал его. При этом он впервые употребил в печати термин «интеграл», указав, что из равенства двух выражений, связывающих дифференциалы, следует равенство интегралов.

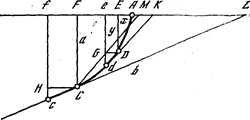В лекциях, читанных Лопиталю, И. Бернулли ход решения излагает так. Пусть искомой кривой будет АDС. Материальная точка за время ∆t перемещается из точки D в точку d и из точки С в точку с. По условию задачи проекции дуг Dd Сс на вертикаль одинаковы. Проведем через D и С касательные к кривой до пересечения с продолжением АF. Отрезки касательных будут DK и CL. Напишем тождество

Dd/Сс=Dd/Hc • Hc/Cc.

Дуги Dd и Сс малы, поэтому фигуры GDd и НСс можно считать треугольниками.

Из подобия треугольников GDd и DEK, НСс и СFL получим

Dd/DG=DK/DE,Сс/Нс=CL/СF.

С помощью этих пропорций найдем

Dd/Сс=DG1Нс • DК/DЕ • СF/СL.

По условиям задачи dG/Нс=1, поэтому

Dd1Сс=DК/DЕ • СF/СL.

Проведем через точку С прямую СМ, параллельную DК. Тогда

DК/DЕ=СМ/СF, Dd/Сс=СМ/СL.

Но отношение Dd/Сс равно отношению скоростей (интервал ∆t один и тот же), квадраты же скоростей, по найденному Галилеем закону, относятся как пройденные высоты; это дает

Dd2/Сс2=СМ2/СL2=DЕ/CF, СМ2/СL2 =DЕ/СF.

Последнее равенство означает, что если через две произвольные точки кривой провести касательные СL и DК и через точку С провести СМ параллельно DК, то должна выполняться указанная пропорция. Таким свойством обладает искомая кривая.

Задача оказалась сведенной к классу обратных задач на касательные: найти кривую, касательные к которой удовлетворяют некоторому требованию. Подобную задачу впервые предложил Декарту Дебон, и Декарт с ней не справился. Разработанный Лейбницем метод позволяет решать и обратные задачи на касательные.

Выберем начало координат в точке А. Обозначим АЕ=х, ЕD=у. Тогда GD=dх, Gd=dу. Обозначим также СF=а, СL=b. Треугольники FСМ и СdD подобны, отсюда

Gd/Dd=FС/СМ.

Но Dd = √dx2+dy2, поэтому

dy/√ dx2+dy2= а/СМ, откуда

CM2= (a2dx2+a2dy2)/dy2.

Подставим найденное выражение в пропорцию СL2/СM2=СF/СЕ и получим дифференциальное уравнение

b2dy2/(a2dx2+a2dy2)=a/y, b2ydy2a3dy2=a3dx2, (b2yа3)dу2 = а3dx2,

√b2ya3 dy=√a3 dx.

В уравнении переменные разделены, интегрирование его дает искомую кривую

2b2у — 2а3/3b2 √b2у а3 == х√а3.

Парацентрическая изохрона оказалась полукубической параболой. Вид кривой раньше Я. Бернулли определили Лейбниц и Гюйгенс, но лишь Я. Бернулли дал решение средствами анализа бесконечно малых.

В приложении к другой работе о рядах (1694 г.) Я. Бернулли сформулировал несколько тезисов.

1. Существуют спирали, которые совершают бесконечное число витков вокруг полюса, но имеют конечную длину.

2. Существуют кривые, которые, подобно эллипсу, замкнуты и, подобно параболе, уходят в бесконечность, например ay2=х2(b+х).

3. Существуют кривые, состоящие из двух ветвей, например ау2=х{а2—х2),

4. Существуют неограниченные поверхности с конечной площадью.

5. Существуют неограниченные поверхности с бесконечной площадью, но такие, что соответствующие им тела вращения обладают конечным объемом.

Я. Бернулли увлекался также и изопериметрическими задачами. Древнейшая из них—задача легендарной основательницы Карфагена и его первой царицы Дидоны. Легенда такова. Дидона бежала от отца, тирского царя, и достигла Африки, где купила у туземцев участок земли на берегу моря «не больше, чем можно окружить воловьей шкурой». Она разрезала шкуру на узкие полоски и связала из них длинную ленту. Спрашивается, какой формы должна быть фигура, оцепленная лентой данной длины, чтобы площадь фигуры была наибольшей?

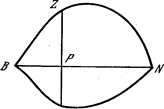ВандерВарден пишет, что Зенодор, живший вскоре после Архимеда, высказал 14 предложений относительно изопериметрических фигур. Он утверждал, что из всех фигур (кругов и многоугольников), имеющих одинаковый периметр, круг будет наибольшим, а также и то, что из всех пространственных тел с одинаковой поверхностью наибольшим будет шар.

Решение задачи содержится в записных книжках Я. Бернулли и помещено в майском номере «Acta Eruditorum» за 1701 г. Я. Бернулли и здесь применил высказанный ранее принцип: поскольку площадь должна быть экстремальной, этим же свойством должна обладать и любая ее элементарная часть. Он получил дифференциальное уравнение третьего порядка и впоследствии проинтегрировал его.

К. А. Рыбников пишет: «Таким образом, решение изопериметрической задачи означало очень важный, принципиально новый этап в истории вариационного исчисления; оно дало возможность решать более сложные вариационные задачи, им был сделан важный шаг на пути решения вариационных задач».

При изучении свойств сочетаний и фигурных чисел Я. Бернулли встретился с суммированием степеней натуральных чисел Sm = å km

Эти вопросы интересовали математиков и ранее. Я. Бернулли составил таблицу фигурных чисел, ук

Учебная работа № 2051. Бернулли