Учебная работа № 1917. Исследование распределения температуры в тонком цилиндрическом стержне

Учебная работа № 1917. Исследование распределения температуры в тонком цилиндрическом стержне

Курсовая работа по информатике

Исполнитель: Солнцев П.В.

СанктПетербургский Государственный Технологический Институт (Технический Университет)

СанктПетербург 2001

В решении любой прикладной задачи можно выделить три основных этапа: построение математической модели исследуемого объекта, выбор способа и алгоритма решения полученной модели, численная реализация алгоритма.

Цель данной работы – на примере исследования распределения температуры в тонком цилиндрическом стержне освоить основные методы приближённых вычислений, приобрести практические навыки самостоятельных исследований, существенно опирающихся на использование методов прикладной математики.

Постановка задачи

Физическая модель

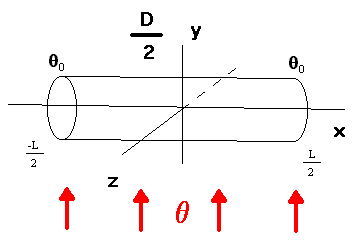
В ряде практических задач возникает необходимость исследования распределения температуры вдоль тонкого цилиндрического стержня, помещённого в высокотемпературный поток жидкости или газа. Это исследование может проводиться либо на основе обработки эксперимента (измерение температуры в различных точках стержня), либо путём анализа соответствующей математической модели.

В настоящей работе используются оба подхода.

Тонкий цилиндрический стержень помещён в тепловой поток с постоянной температурой , на концах стержня поддерживается постоянная температура ₀ .

1.2 Математическая модель

Совместим координатную ось абсцисс с продольной осью стержня с началом в середине стержня. Будем рассматривать задачу (распределения температуры по стержню) мосле момента установления режима Т₀ .

Первая математическая модель использует экспериментальные данные, при этом измеряют температуру U_i стержня в нескольких точках стержня с координатами x_i . Результаты измерения U_i рассматривают как функцию регрессии и получают статистики. Учитывая чётность U(x) можно искать её в виде многочлена по чётным степеням x (ограничимся 4ой степенью этого многочлена).

(1.1)

Задача сводится к отысканию оценок неизвестных параметров, т.е. коэффициентов a₀ , a₁ и a₂ , например, методом наименьших квадратов.

Вторая математическая модель, также использующая экспериментальные данные, состоит в применении интерполяционных формул и может употребляться, если погрешность измерений температуры Ui пренебрежимо мала, т.е. можно считать, что U(x_i )=U_i

Третья математическая модель основана на использовании закона теплофизики. Можно доказать, что искомая функция U(x) имеет вид:

(1.2)

где коэффициент теплопроводности, коэффициент теплоотдачи, D – диаметр стержня, температура потока, в который помещён стержень.

Ищем U(x) как решение краевой задачи для уравнения (1.2) с граничными условиями:

(1.3)

на отрезке [L|/2;L/2], где L – длина стержня, _ постоянная температура, поддерживаемая на концах стержня.

Коэффициент теплопроводности  зависит от температуры:

(1.4)

где _ начальное значение коэффициента теплопроводности, _ вспомогательный коэффициент.

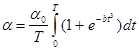Коэффициент теплоотдачи вычисляют по формуле:

(1.5)

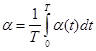т.е. как среднее значение функции

за некоторый отрезок времени от 0 до Т, здесь _ значение при t стремящемся к бесконечности, b – известный коэффициент.

Время Т₀ , по истечении которого распределение температуры в стержне можно считать установившимся определяется по формуле:

(1.6)

где а – коэффициент температуропроводности, наименьший положительный корень уравнения:

(1.7)

Задание курсовой работы

Вариант № 136

Исходные данные:

L = 0.0386 м

D = 0,00386 м

^о С

_ ^о С

_ 141,85 (Вт/м*К)

_ 2,703*10⁴

6,789*10⁷

_ 3,383*102 (Вт/м² *К)

218 ^о С

А = 3,043*105 (м² /с)

11

X, м	U, o C
0	353
0,00386	343
0,00772	313
0,01158	261
0,01544	184
0,01930	74

2. Обработка результатов эксперимента.

2.1 Задача регрессии. Метод наименьших квадратов.

Ищем функцию регрессии в виде (1.1). Оценки коэффициентов находим с помощью МНК, при этом наименьшими будут оценки, обеспечивающие минимум квадратов отклонений оценочной функции регрессии от экспериментальных значений температуры; суммирование ведут по всем экспериментальным точкам, т.е. минимум величины S:

(2.1)

В нашем случае необходимым т достаточным условием минимума S будут:

Где k = 0, 1, 2. (2,2)

Из уравнений (2.1) и (2.2) получаем:

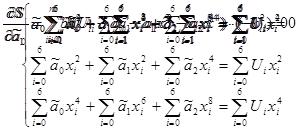(2.3)

Сумма

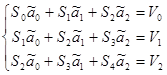Система (2.3) примет вид:

(2.4)

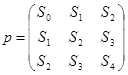В результате вычислений получаем S_k и V_j . Обозначим матрицу коэффициентов уравнения (2.4) через “p”:

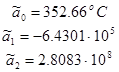Методом Гаусса решаем систему (2.4) и найдём обратную матрицу p¹ . В результате получаем:

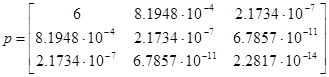Подставляя в (2.1) найденные значения оценок коэффициентов а_к , находим минимальное значение суммы S:

S_min =0.7597

При построении доверительных интервалов для оценок коэффициентов определяем предварительно точечные оценки.

Предполагается, что экспериментальные значения x_i измерены с пренебрежимо малыми ошибками, а случайные ошибки измерения величины U_i независимы и распределены по нормальному закону с постоянной дисперсией ^ , которая неизвестна. Для имеющихся измерений температуры U_i неизвестная дисперсия оценивается по формуле:

Где r – число степеней свободы системы, равное разности между количеством экспериментальных точек и количеством вычисляемых оценок коэффициентов, т.е. r = 3.

Оценка корреляционной матрицы имеет вид:

Оценки дисперсий параметров оценок коэффициентов найдём по формулам:

Где S_k – минор соответствующего диагонального элемента матрицы нормальной системы;

 главный определитель нормальной системы.

В нашем случае:

S₀ =3.5438 10²²

S₁ =8.9667 10¹⁴

S₂ =6.3247 10⁷

Откуда:

Найденные оценки коэффициентов распределены по нормальному закону, т.к. линейно зависят от линейно распределённых экспериментальных данных Ui.

Известно, что эти оценки несмещённые и эффективные. Тогда случайные величины:

Имеют распределения Стьюдента, а r = 3.

Выбираем доверительную вероятность =0,9 и по таблице Стьюдента находим критическое значение _ равное 2,35, удовлетворяющее равенству:

Доверительные интервалы для коэффициентов:

(2.4*)

В нашем случае примут вид:

2.2 Проверка статистической гипотезы об адекватности модели задачи регрессии.

Имеется выборка объёма n экспериментальных значений (x_i ;U_i ). Предполагаем, что ошибки измерения x_i пренебрежимо малы, а случайные ошибки измерения температур U_i подчинены нормальному закону с постоянной дисперсией ^ Мы выбрали функцию регрессии в виде:

Выясним, нельзя ли было ограничиться многочленом второго порядка, т.е. функцией вида:

(2.5)

C помощью МНК можно найти оценки этих функций и несмещённый оценки дисперсии отдельного измерения Ui для этих случаев:

Где r₁ = 4 (количество точек – 6, параметра – 2).

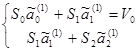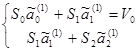Нормальная система уравнений для определения новых оценок коэффициентов функции (2.5)с помощью МНК имеет вид:

(2.7)

Решая эту систему методом Гаусса, получим:

(2.8)

Чем лучше функция регрессии описывает эксперимент, тем меньше для неё должна быть оценка дисперсии отдельного измерения Ui, т.к. при плохом выборе функции в дисперсию войдут связанные с этим выбором дополнительные погрешности. Поэтому для того, чтобы сделать выбор между функциями U(x) и U(1)(x) нужно проверить значимость различия между соответствующими оценками дисперсии, т.е. проверить гипотезу:

Н0 – альтернативная гипотеза

Т.е. проверить, значимо ли уменьшение дисперсии при увеличении степени многочлена.

В качестве статического критерия рассмотрим случайную величину, равную:

(2.9)

имеющую распределение Фишера с(r ; r₁ ) степенями свободы. Выбираем уровень распределения Фишера, находим критическое значение F^* _ , удовлетворяющее равенству: p(F>F^* _ =

В нашем случае F=349.02, а F^* _ =10,13.

Если бы выполнилось практически невозможное соотношение F>F_ , имевшее вероятность 0,01, то гипотезу Н₀ пришлось бы отклонить. Но в нашем случае можно ограничиться многочленом

, коэффициенты в котором неодинаковы.

3. Нахождение коэффициента теплопроводности .

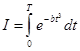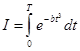Коэффициент вычислим по формуле (1.5), обозначим:

(3.1)

Определим допустимую абсолютную погрешность величины интеграла I, исходя из требования, чтобы относительная погрешность вычисления не превосходила 0,1%, т.е.:

(3.2)

Т.к. из (3.1) очевидно, что _ , то условие (3.2) заведомо будет выполнено, если:

(3.3)

Т.е. в качестве предельно допустимой абсолютной погрешности вычисления интеграла I возьмём 0,001Т (3.4)

Т=218 ^о С, следовательно, 0,218 ^о С.

3.1 Вычисление интеграла I методом трапеции

Использование теоретической оценки погрешности

Для обозначения требуемой точности количества частей n, на которые нужно разбить отрезок интегрирования [0;T] определяется по формуле:

, где M_ [f”(t)], te [0;T], f(t)=e ^{bt 3}

Учитывая формулу (3.4) получаем:

(3.5)

Дифференцируя f(t), получим:

А необходимое условие экстремума: f”(t)f’’’(t)=0, откуда получаем:

Учебная работа № 1917. Исследование распределения температуры в тонком цилиндрическом стержне