(6 оценок, среднее: 4,67 из 5)
Загрузка...
Учебная работа № 1773. Элементарные частицы и космология
В работе с единой точки зрения рассмотрены вопросы организации живой и неживой материи, делается предположение об эквивалентности этих понятий. Делается попытка нового взгляда на такие понятия, как масса, пространство и время. В основе пересмотра этих понятий лежит предположение, что вакуум представляет собой 4мерную жидкости. Данное предположение возникло при анализе возможных механизмов процесса движения элементарной частицы. Также сделаны выводы о единообразии микромира и макромира и на их основе попытка качественного анализа живых и информационных систем, как квантовых объектов.
На сегодняшний день в науке наблюдается определенный кризис. Кризис естественный и, повидимому, связан с индустриализацией, точнее даже коммерциализацией, науки, превращения ее в отрасль народного хозяйства, ориентированной на производство ликвидных товаров. Это не хорошо и не плохо, но в такой ситуации главной становится технологическая сторона и прикладной характер любых научных исследований. В то же время, такие фундаментальные вопросы, как время, материя, жизнь и смерть и т.д., остаются в тени.
Интуитивно человек чувствует неслучайность существования мира и универсальность законов его устройства, но современные научные теории слишком разрознены, наука поделена на разделы, которые слабо связаны между собой. Особенно это видно на примере физики и медицинских наук или биологии, где даже не обосновывается, каким образом набор неживых элементов (молекул, атомов) образуют живой организм, жизнь для него воспринимается как данность. То же самое относительно других научных дисциплин. Тем не менее, внутреннее ощущение подсказывает, что должны существовать общие принципы и законы и одна основа для всех этих направлений. В частности, на определенные размышления наводит огромное количество элементарных частиц в физической теории, наверное, один из самых серьезных критических моментов в ней. Такие же чувства вызывает наличие в современных теориях таких понятий, как вакуум и силы взаимодействия. Собственно эти вопросы и ставятся в данной работе, и по мере возможности, делается попытка ответить на них.
Начнем с рассмотрения механизма движения объектов в пространстве. Будем считать объекты элементарными частицами, элементарными в классическом понимании, то есть в виде твердых бесструктурных шариков, размеры шариков могут быть и конечными и бесконечными, как увидим далее, это не влияет на характер движения.
Для этого рассмотрим такой пример. Пусть частица двигается из точки a в точку b с конечной скоростью (рис. 1). Подразумеваем, что частица в процессе движения будет находиться на линии траектории движения, правильнее, наверное даже сказать, что при движении частицы из a в b можно говорить о траектории движения. Действительно, считая, что время и пространство непрерывным, можем уменьшать расстояние dr между a и b и промежуток времени dt до бесконечно малых величин. Так как мы условились считать частицы бесструктурными, и кроме того, мы верим в законы сохранения материи и энергии, то в пределе рассмотрения, когда 
и 
, частица никогда не сможет покинуть точку a, либо должна находится в любой точке траектории своего движения, то есть “размазываться” по траектории, этот парадокс известен как “парадокс Зенона”. В чем же причина такого парадокса в отношении элементарных частиц, ведь опыт показывает обратное частицы всегда находятся в движении? Причины, повидимому, кроются в неправильности исходных предположений: либо предположение о непрерывности пространствавремени неверно, либо движение частицы происходит без переноса материи в классическом понимании материи.
Если первое предположение неверно, то можно сделать вывод, что пространствовремя имеет дискретную структуру. В этом случае должны существовать элементарные промежуток времени 
и расстояние 
, но тогда следует пересмотреть механизм движения частиц и само представление о материальной частице. Необходимо уточнить, что подразумевается под дискретным пространством временем. Здесь также может быть несколько моделей такого пространства, но их, в принципе, можно свести к двум. Первая модель представляет пространство в виде решетки, а вторая предполагает непрерывное пространство при наличии квантов времени и длины.
В первой модели пространствовремя или пространство и время в отдельности, не могут представлять собой жесткую сетку, в узлах которой только и могут находится частицы, так как в этом случае вопервых невозможно взаимодействие между частицами, вовторых, ни элементарное расстояние 
, ни элементарный промежуток времени 
, не имеют никакого значения, так как пространство между узлами решетки не влияет на объекты в пространстве узлов решетки, втретьих пространство становится анизотропным, причем анизотропные свойства должны зависеть от вида решетки (кубическая, октаэдровая и т.д.) и, вчетвертых, ни о каких волновых свойствах частиц не может быть и речи.
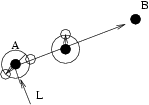
Рис.1 Движение частицы в дискретном пространствевремени
Рассмотрим вторую модель, в которой пространствовремя непрерывно, но имеется элементарные промежутки времени и расстояния. В таком пространстве, любая частица будет двигаться только “скачками”, то есть через определенные интервалы (кванты времени) частица появляется на расстоянии L от предыдущего своего положения (рис.1), причем появлению частицы в одной точке пространства должно предшествовать исчезновение её в предыдущей по времени точке пространства. Сейчас не имеет значения величины кванта времени и расстояния, важен процесс движения. Сразу возникают следующие вопросы: в каком направлении должна двигаться частица и что происходит с частицей в промежутке времени между исчезновением в точке a и появлением ее в точке b, чтобы не нарушались законы сохранения. Предположим, что в момент, следующий за исчезновением частицы в точке a, вся материя частицы на самом деле не исчезла, а перешла в иную форму. То есть мы предполагаем, что эта материя фактически, “растворилась” в вакууме, причем через некоторый элементарный промежуток, она снова должна возникнуть, но уже на элементарном расстоянии от предыдущего положения. При этом, в силу известной изотропии пространства, направления следующего появления частицы абсолютно эквивалентны, следовательно частица опять не сможет покинуть своего положения, а будет появляться в окрестностях точки a, что, опятьтаки, противоречит наблюдениям. Из всех этих рассуждений можно сделать вывод о том, что и эти модели не отражают действительности. Но эти модели построены были исходя из представления о частицах, как бесструктурных элементах. Теперь можно сделать предположение, что частицы могут обладать некоторой структурой, то есть в такой модели, они уже не будут элементарными.
На сегодняшний день достоверно установлены, доказаны и используются в технике и науке волновые свойства материи, впрочем, дальше придется уточнить само понятие материи. Суть волновых свойств материи пока не выяснена, однако совершенно логично предполагать, что для распространения любой волны необходима какаялибо среда, причем обладающая структурой или, подругому, локальными характеристиками. Иными словами эта среда должна быть материальной. Так как мы рассматриваем волны материи, естественно такой средой для них является вакуум; в этом нет ничего удивительного, вакуум в физике уже несколько десятилетий считается видом материи, правда весьма специфическим. Одной из характеристик вакуума, как известно, является его изотропия, в силу установленной изотропии пространства. Кроме того, в дальнейших рассуждениях, нам понадобиться такое явление, как универсальность волновых свойств материи, независимо от её вида. То есть то, что любой материальный объект должен обладать волновыми свойствами. Из этих исходных предположений, можно сделать вывод о том, что вакуум в действительности является сплошной средой, и, кроме того, обладает локальными характеристиками, то есть является средой, способной к распространению волн. Далее, сделаем еще одно небольшое, но очень важно предположение, будем считать, что физический вакуум обладает текучестью, то есть обладает свойствами жидкости.
Немного отвлечемся от вопроса природы вакуума и обратимся к теме измерения, точнее даже не измерения, а получения информации и восприятия. Этот вопрос очень интересен сам по себе и, как увидим далее, приводит к довольно интересным выводам. К тому же этот вопрос уж очень набил оскомину, и воспринимается как какоето колдовство и магия.
Как уже было сказано, процесс измерения есть не что иное, как процесс получения информации об измеряемом объекте. Соответственно, в любом измерении должны участвовать как минимум два объекта: собственно объект измерения и измерительный прибор. Здесь нужно сделать одно замечание, касающееся прибора, принципиально ни один прибор не в состоянии определять значения величин с абсолютной точностью, в этом случае было бы необходимо наличие элементов прибора с “нулевыми” и элементов с “бесконечными” размерами, что противоречит природе физических объектов.
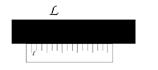
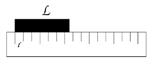
Рис.2 Иллюстрация к измерению длины объекта
Для изучения этого вопроса обратимся к самому простому и понятному примеру: измерению линейных размеров объекта [рис. \ref{vol_fig}]. В качестве прибора в данном случае выступает линейка. Прибор имеет две характеристики: первая это цена деления l, вторая это собственно размеры прибора (количество делений), обозначим ее как Z. Измеряемый объект будет характеризоваться единственной величиной длиной L. В действительности у объекта может быть множество характеристик, но мы не сможем их измерить данным прибором (линейкой) непосредственно.
Теперь можно рассмотреть в подробности процесс измерения размера объекта. Предположим, что размер объекта L меньше размера прибора, тогда проведя измерение, можно установить, что размер объекта составляет L/l единиц. Обозначим m размер объекта в единицах прибора.
При этом реальный размер будет отличаться от измеренного на величину до l. То есть ошибка измерения составит l. Можно уменьшить ошибку измерения, уменьшая цену деления прибора, но в любом случае цена деления будет отлична от нуля, иначе нет смысла в измерении длины. Мало того, цена деления не может быть также и бесконечно малой, так как мы имеем дело с физическим прибором, то есть с реальной и материальной линейкой, то для такой линейки цена деления может быть уменьшена до конечных значений, а ограничения на величину деления может накладывать например размер молекул вещества из которой она сделана.
Так как размер измеряемого объекта меньше размера прибора, то в этом случае его длина может быть в принципе измерена.
Что касается ситуации, когда размер прибора меньше измеряемого размера объекта, то в этом случае вообще невозможно измерить объект и для прибора такой объект не будет иметь линейных свойств. Что это означает? Это означает, что поведение объекта (в данном случае его линейные размеры), зависит от того, с каким прибором он взаимодействует, при этом его собственные реальные свойства остаются неизменными. Действительно, если размер линейки меньше размера прибора это вовсе не означает, что они отсутствуют, отсутствуют они только для данной конкретной линейки.
Если продолжить наши рассуждения дальше и считать любое взаимодействие двух и более объектов, как взаимное измерение, то можно предположить, что один и тот же объект будет проявлять себя по разному в различных взаимодействиях. Если говорить об элементарных частицах, то известный дуализм “волначастица” в этом случае абсолютно нормальное явление, так как характеризует то, какое происходит взаимодействие, а не является свойством частицы.