Учебная работа № 1743. Исследование наилучших приближений непрерывных периодических функций тригонометрическими полиномами
Государственный комитет Российской Федерации по высшему образованию
Саратовский ордена Трудового Красного Знамени государственный университет им. Н.Г.Чернышевского
Кафедра математического анализа
ИССЛЕДОВАНИЕ НАИЛУЧШИХ ПРИБЛИЖЕНИЙ НЕПРЕРЫВНЫХ ПЕРИОДИЧЕСКИХ ФУНКЦИЙ ТРИГОНОМЕТРИЧЕСКИМИ ПОЛИНОМАМИ
ДИПЛОМНАЯ РАБОТА
студентки 524 группы механикоматематического факультета
Чуркиной Любови Васильевны
Научный руководитель
к.ф.м.н, доцент
Тимофеев В. Г.
Заведующий кафедрой
доктор ф.м.н., профессор
Прохоров Д.В.
г.Саратов1996 г.
.
| Наименование | Стр. |
| 3 | |
| §1. Некоторые вспомогательные определения | 7 |
| §2. Простейшие свойства модулей нерперывности | 20 |
| §3. Обобщение теоремы Джексона | 24 |
| §4. Обобщение неравенства С.Н.Бернштейна | 27 |
| §5. Дифференциальные свойства тригонометрических полиномов, аппроксимирующих заданную функцию | 30 |
| §6. Обобщение обратных теорем С. Н. Бернштейна и Ш. ВаллеПуссена | 34 |
| §7. Основная теорема | 44 |
| §8. Решение задач | 47 |
| Литература | 50 |
Дипломная работа посвящена исследованию наилучших приближений непрерывных периодических функций тригонометрическими полиномами. В ней даются необходимые и достаточные условия для того, чтобы наилучшие приближения имели заданный (степенной) порядок убывания.
Дипломная работа носит реферативный характер и состоит из “Введения” и восьми параграфов.
В настоящей работе мы рассматриваем следующие задачи:
1.При каких ограничениях на непрерывную функцию F (u )(1 £ u £+1) её наилучшие приближения En [F ;1,+1] обыкновенными многочленами имеют заданный порядок j (n1 )?
2.При каких ограничениях на непрерывную периодическую функцию f (x ) её наилучшее приближение En [f ] тригонометрическими полиномами имеют заданный порядок j (n1 )?
Подстановка u=cos(x) сводит задачу 1 к задаче 2. Достаточно, следовательно, рассматривать лишь задачу 2.
Мы ограничимся случаем, когда j (d )ÎN a , для некоторого a , где j (d ) функция сравнения рго порядка и для 0<d <h £p
![]()
С.Н.Бернштейн, Д.Джексон и Ш.ВаллеПуссен получили зависимости между оценками сверху для En [f ] и дифференциальными свойствами f . Некоторые дополнения к их теоремам доказаны А.Зигмундом. нам предстоит, поэтому, получить зависимости между дифференциальными свойствами f и оценками En [f ] снизу. Впервые задачами типа 1 занимался С.Н.Бернштейн. А именно, им получено ассимптотическое равенство:
![]() ,
,
где m некоторое число.
Наша основная теорема формулируется следующим образом:
Пусть j ÎN a .Для того чтобы
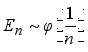
необходимо, чтобы для любого натурального k> a, и достаточно, чтобы для некоторого натурального k> a
![]()
где ![]()
Изложим теперь кратко содержание каждого из параграфов работы.
В §1 даётся ряд вспомогательных определений, которые понадобятся в дальнейшей работе.
В §2 выводятся основные свойства модулей непрерывности высших порядков. Почти все эти свойства используются в дальнейшем тексте.
§3 посвящен обобщению теоремы Джексона. Как известно, Джексон доказал следующую теорему: если f имеет непрерывную rую производную f (r) , то
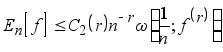
Таким образом, теорема Джексона дает оценку сверху для наилучших приближений, если известны дифференциальные свойства аппроксимируемой функции.
В 1947 г. появилась работа С.Н.Бернштейна [1]. Одна из теорем этой работы содержит в качестве следствия такое предложение: пусть
![]()
Тогда
![]()
В §3 доказываем:
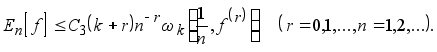
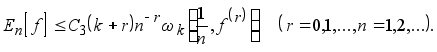
В §4 формулируется доказанное в работе С.Б.Стечкина [2] обобщение известного неравенства С.Н.Бернштейна [3], [4] для производных от тригонометрического полинома. Мы приводим затем ряд следствий из нашего неравенства (*). Они играют существенную роль при доказательстве теорем §5.
В §5 рассматривается следующая задача. Пусть тригонометрический полином tn , близок в равномерной метрике к заданной функции f или последовательность полиномов {tn } достаточно хорошо аппроксимирует заданную функцию f . Как связаны тогда дифференциальные свойства f с дифференциальными свойствами tn ?
Если tn , образуется из f посредством регулярного метода суммирования рядов Фурье, то ответ тривиален: для того чтобы ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Оказывается, что этот результат сохраняется и для полиномов наилучшего приближения: для того, чтобы ![]()
![]()
![]()
![]()
![]()
Отметим еще один результат параграфа: для того чтобы ![]()
![]()
![]()
![]()
§6 посвящён “обратным теоремам” теории приближения.
Известно предложение: пусть
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Тогда, если a не целое, r= [a ], b =a r , то f имеет нерперывную производную ![]()
![]()
Случай целого a рассмотрен Зигмундом. В этом случае
![]()
![]()
Нетрудно показать, что эти два предложения эквивалентны следующему: пусть 0<a <k и
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Тогда
![]()
![]()
В работе [3] С.Н.Бернштейн доказал также эквивалентность условий 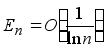
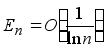
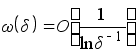
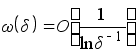
Мы переносим эти теоремы на условия вида
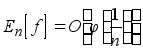
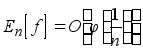
где j ÎN a .
Кроме того, в этом параграфе доказано, например, такое предложение: пусть k натуральное число и
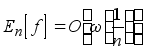
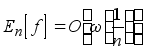
для того, чтобы ![]()
![]()
![]()
![]()
![]()
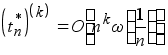
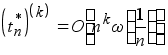
В конце параграфа даются уточнения теорем ВаллеПуссена.
В §7 доказывается основная теорема. Мы даём здесь же оценку En [f ] снизу, если


Именно, тогда
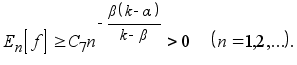
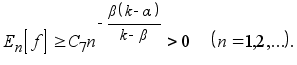
Случай a =0 установлен С.Н.Бернштейном [3].
В §8 мы рассматриваем несколько решений задач с использованием различных модулей непрерывности.
§1. Некоторые вспомогательные определения.
В работе рассматриваются непрерывные функции f с периодом 2p и их приближение тригонометрическими полиномами. Через tn (x )обозначается тригонометрический полином порядка не выше n , а через tn * (x )=tn * (x,f )тригонометрический полином, наименее уклоняющийся от f среди всех tn (x) . Мы полагаем ![]()
![]()
![]()
![]()
Введём ряд определений.
Определение 1. При каждом фиксированном ![]()
![]()
![]()
![]()
где С8 какаянибудь положительная постоянная, которая не зависит от d и которая, вообще говоря, является различной для разных функций. Этот класс обозначается H a или Lip a .
Определение 2. Обозначим при фиксированном натуральном r через W(r) L класс функций f , которая имеет абсолютно непрерывные производные до (r 1) порядка и у которой r я производная принадлежит классу L .
Определение 3. Для непрерывной на [a,b ] функции f (x )назовём модулем непрерывности первого порядка или же просто модулем непрерывности функцию w (d )= w (f; d ), определённую на [0, ba ] при помощи следующего равенства:
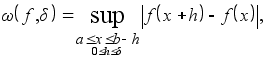
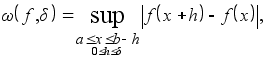
или, что то же самое,
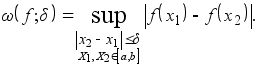
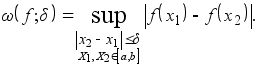
Свойства модуля непрерывности :
1.w(0)=0;
2.w(d) есть функция, монотонно возрастающая;
3.w(d) есть функция непрерывная;
4.w(d) есть функция полуаддитивная в том смысле, что для любых ![]()
![]()
![]()
![]()
![]()
![]()
Доказательство. Свойство 1) вытекает из определения модуля непрерывности.
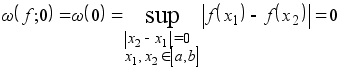
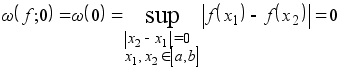
Свойство 2) вытекает из того, что при больших d нам приходится рассматривать sup на более широком множестве значений h . Свойство 4) следует из того, что если мы число ![]()
![]()
![]()
![]()
![]()
![]()


Из неравенства (1.2) вытекает, что если ![]()
![]()
![]()
![]()
![]()
![]()
Теперь докажем свойство 3). Так как функция f (x ) равномерно непрерывна на [a,b ], то ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
а это и означает, что функция w ( d ) непрерывна.
Определение 4. Пусть функция f (x )определена на сегменте [a,b ]. Тогда для любого натурального k и любых ![]()
![]()
![]()
![]()
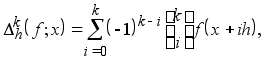
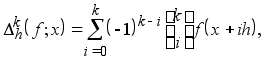
а при ![]()
![]()
![]()
![]()
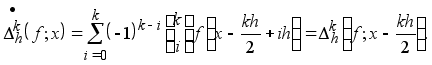
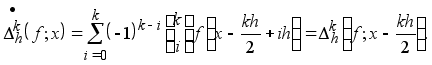
Лемма 1. При любых натуральных j и k справедливо равенство
![]()
![]()
Доказательство. Действительно, так как при любом натуральном k
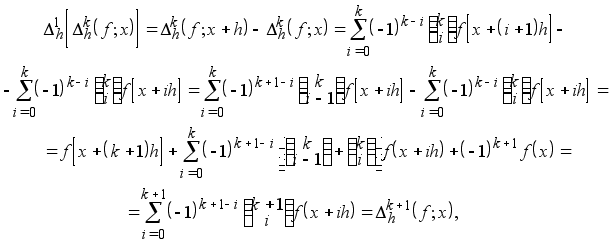
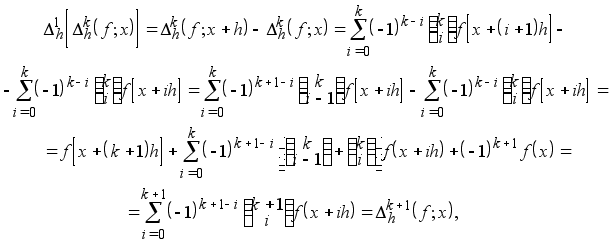
то


Лемма доказана.
Лемма 2. При любых натуральных k и n верна формула:


Доказательство. Воспользуемся индукцией по k . При k= 1 тождество (1.6) проверяется непосредственно:


Предполагая его справедливость при k 1 (k ³2), получим


Лемма доказана.
Определение 5. Если измеримая периода (ba ) функция f (x )ÎLq (Lq класс всех вещественных измеримых на [a,b ] функции f (x )), то под её интегральным модулем гладкости порядка k ³1 понимают функцию
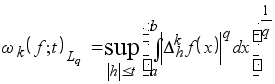
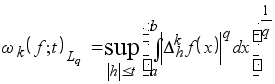
Лемма 3. Если ![]()
![]()
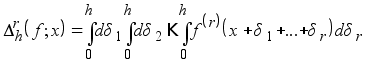
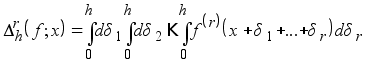
Доказательство. В самом деле,
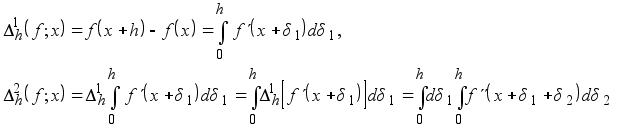
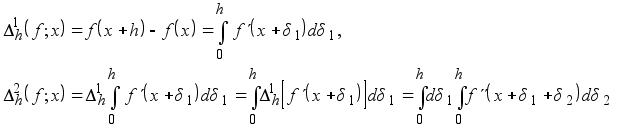
и так далее. Лемма доказана.
Определение 6. Если функция f(x) ограничена на [a,b ], то под её модулем гладкости порядка k ³1 понимают функцию


заданную для неотрицательных значений ![]()
![]()
Свойства модулей гладкости:
1.![]()
![]()
2.![]()
![]()
![]()
3.![]()
![]()
![]()

 (6 оценок, среднее: 4,67 из 5)
(6 оценок, среднее: 4,67 из 5)