Учебная работа № 1715. Интегрирование линейного дифференциального уравнения с помощью степенных рядов
Д![]()
![]() ля решения дифференциального уравнения:
ля решения дифференциального уравнения:
(I.1)
где функции аi(t) (i=0,1,2) разлагаются в степенной ряд в окрестности точки t0 с радиусами сходимости ri :

i=0,1,2
необходимо найти два линейнонезависимых решения 1(t), 2(t). Такими решениями будут, например, решения уравнения (I.1) с начальными условиями:
![]()
![]()
Решения i будем искать в виде степенного ряда:
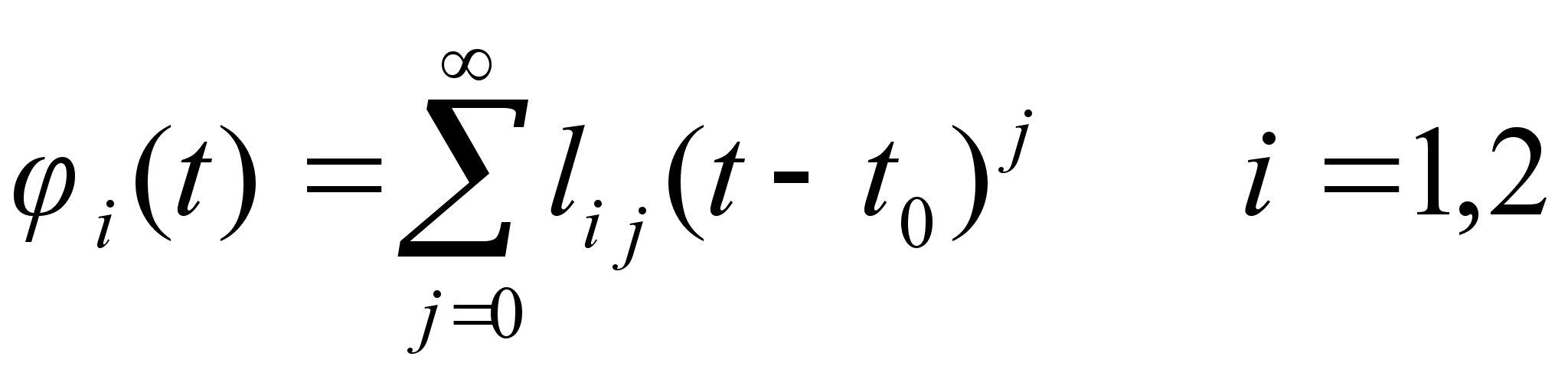
(I.2)
методом неопределенных коэффициентов.
Для решения воспользуемся теоремами.
Теорема 1: (об аналитическом решении)
Если p0(x), p1(x), p2(x) являются аналитическими функциями x в окрестности точки x=x0 и p0(x)≠0, то решения уравнения p0(x)y’’ + p1(x)y’ + p2(x)y = 0 также являются аналитическими функциями в некоторой окрестности той же точки и, значит, решения уравнения можно искать в виде: y=l0 + l1(xx0) + l2(xx0)2 + … + ln(xx0)n + …
Теорема 2: (о разложимости решения в обобщенный степенной ряд)
Если уравнение (I.1) удовлетворяет условиям предыдущей теоремы, но x=x0 является нулем конечного порядка S функции a0(x), нулем порядка S1 или выше функции a1(x) (если S>1) и нулем порядка не ниже S2 коэффициента a2(x) (если S>2), то существует, по крайней мере, одно нетривиальное решение уравнения (I.1) в виде суммы обобщенного степенного ряда:
y= l0(x x0)k + l1(x – x0)k+1 + … + ln(xx0)k+n + …
где k некоторое действительное число, которое может быть как целым, так и дробным, как положительным, так и отрицательным.
Рассмотрим уравнение:
![]() (I.3)
(I.3)
a0(t) = t + 2 ; a1(t) = 1; a2(t) = 4t3; a0(t) ≠ 0 ![]() t
t
по теореме 2 хотя бы одно нетривиальное решение уравнения (I.3) может быть найдено в виде суммы обобщенного степенного ряда ![]()
![]()
![]()
![]()
![]()
![]()
![]()
возьмем t0 = 0, будем искать решение в виде ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Опираясь на теорему 1 и, дифференцируя ряд (I.4) почленно два раза, получим
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(2+t)( ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Вычислим коэффициенты при соответствующих степенях:
t0 : 4c2 – c1=0 ![]()
![]()
![]()
![]()
![]()
![]()
t1 : ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
рекуррентное соотношение имеет вид
![]()
![]()
![]()
![]()
![]()
![]()
![]()
при n=0, ![]()
![]()
n=1, ![]()
![]()
n=2, c4=0
n=3, ![]()
![]()
n=m2, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Найдем радиусы сходимости R полученных решений, общим методом не представляется возможным, поэтому на основании теоремы о существовании и единственности решения.
![]()
![]()
![]()
![]()
![]()
![]()
Которые имеют область сходимости (по формуле Даламбера):
а) 


![]()
![]()
![]()
![]()
![]()
![]()
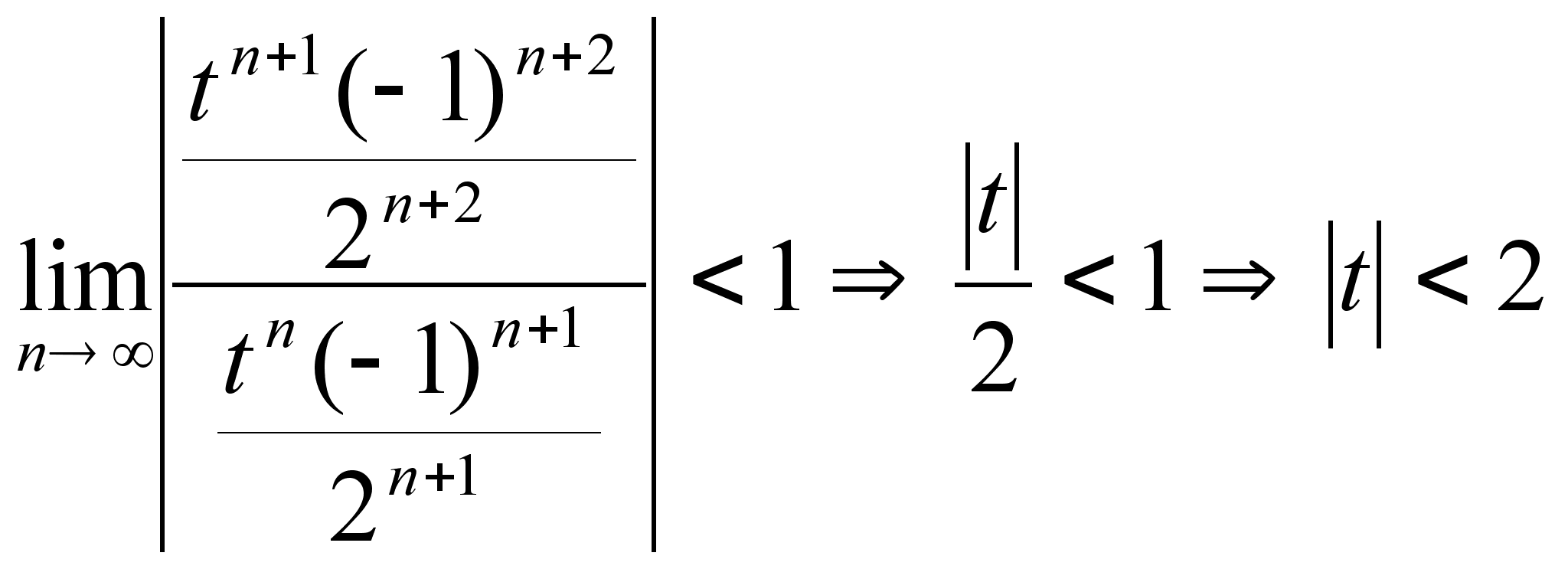
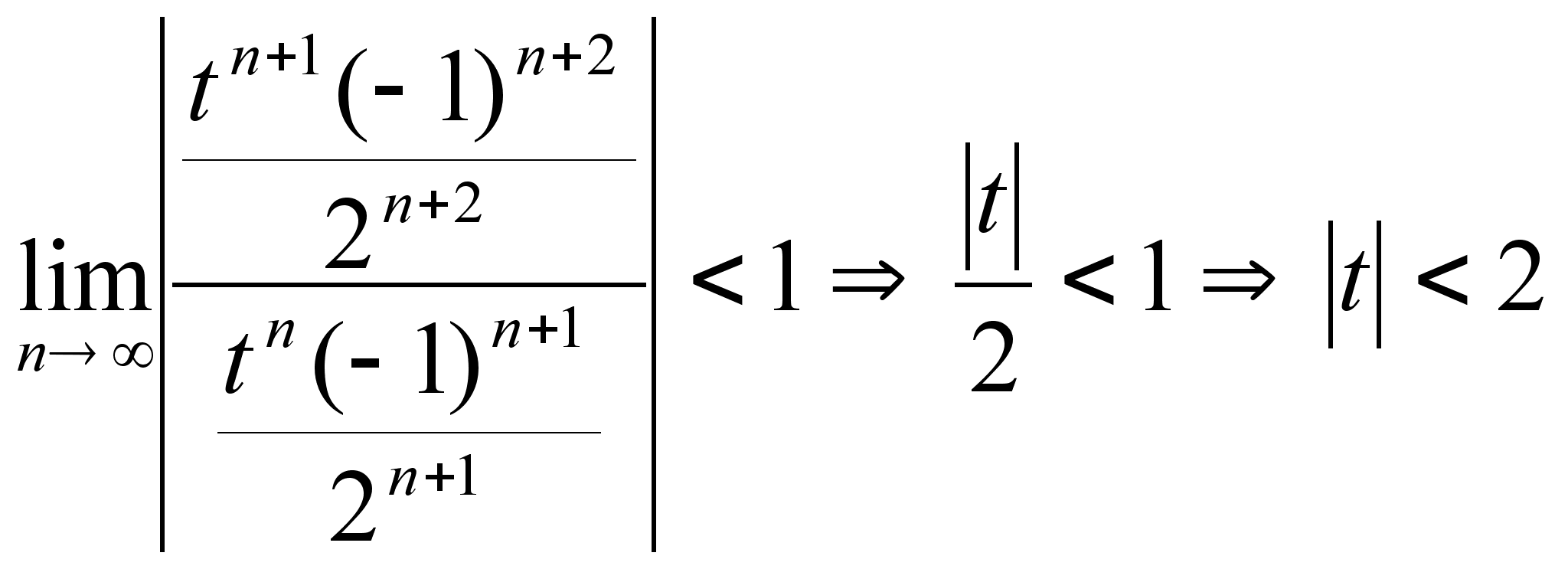
![]()
![]()
![]()
![]()
![]()
![]()
![]()
б) 


![]()
![]()
![]()
![]()
![]()
![]()
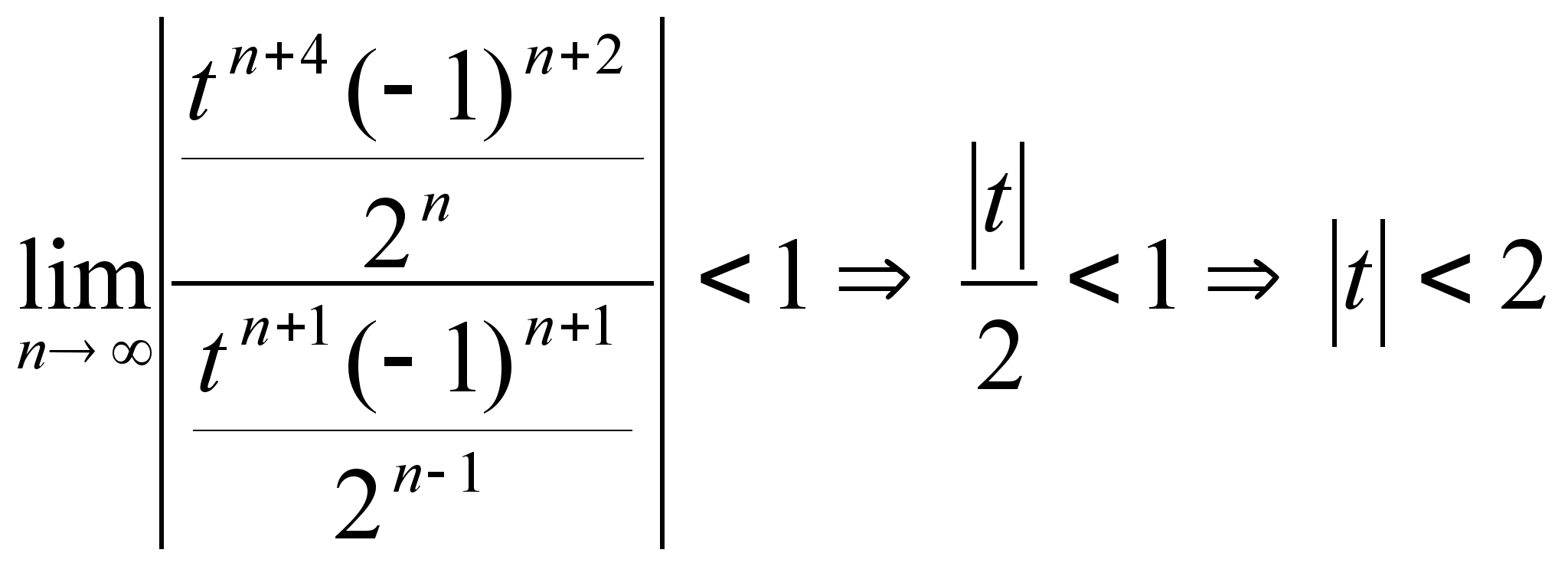
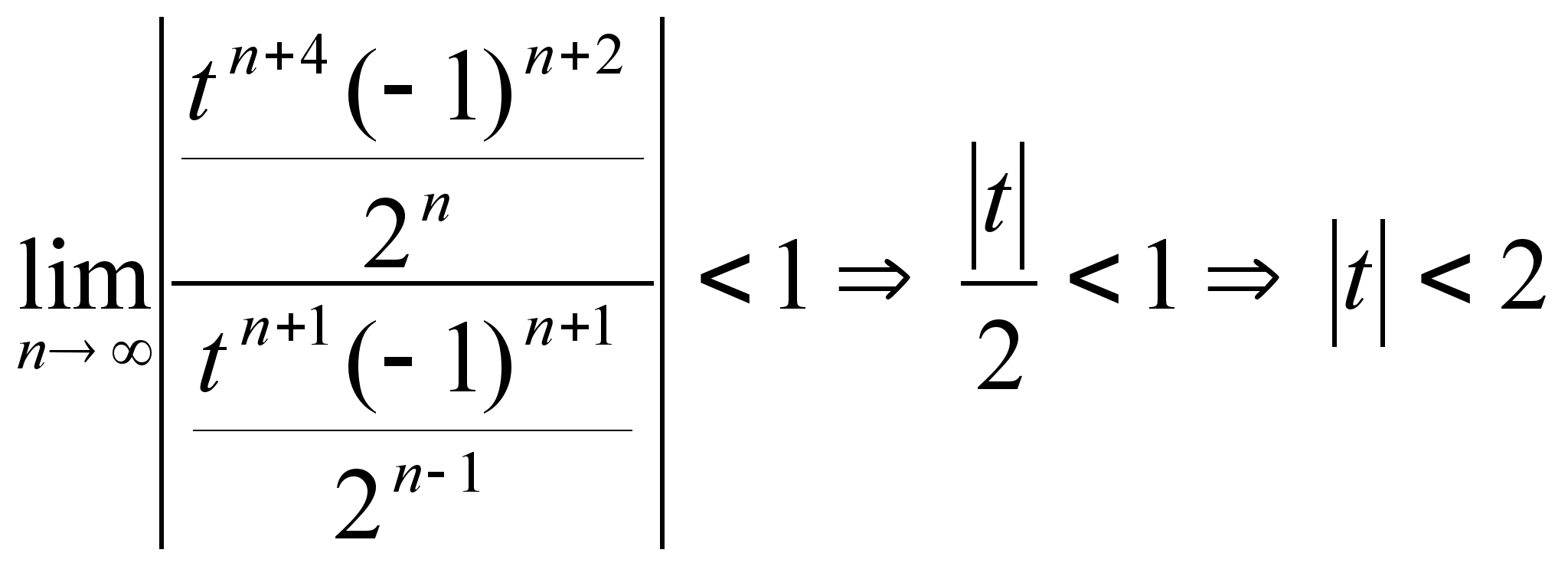
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Итак, область сходимости ![]()
![]()
-
Синтез управления с не более, чем с одним переключением в управляемой системе второго порядка.
Необходимо рассмотреть линейную управляемую систему:
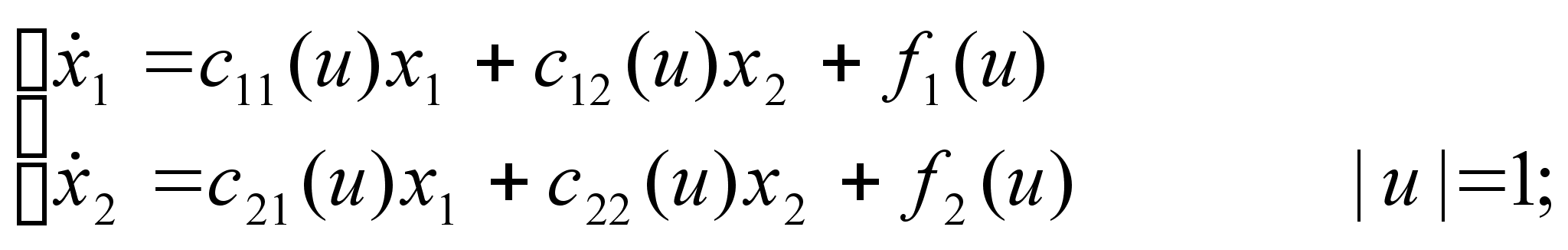
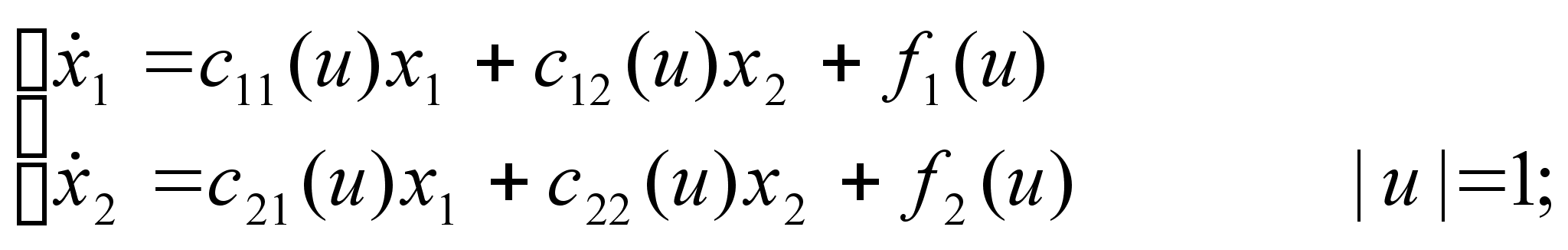
Требуется подобрать управление и( ), переводящее фазовую точку (х1,х2) из заданного начального состояния в начало координат (0,0).
На выбор управления и( ) накладывается условие | и( )|=1 и и( ) имеет не более одного переключения.








![]()
![]()
![]()
![]()
III. Малые возмущения системы линейных уравнений
В этой задаче рассматривается система:
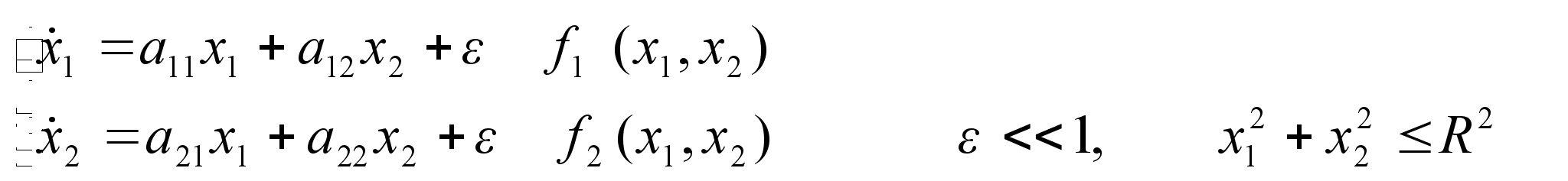
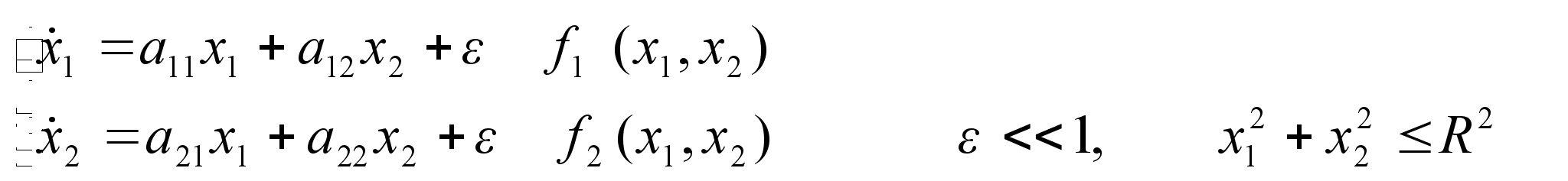
с действительными коэффициентами аij.
Необходимо исследовать фазовые кривые этой системы:
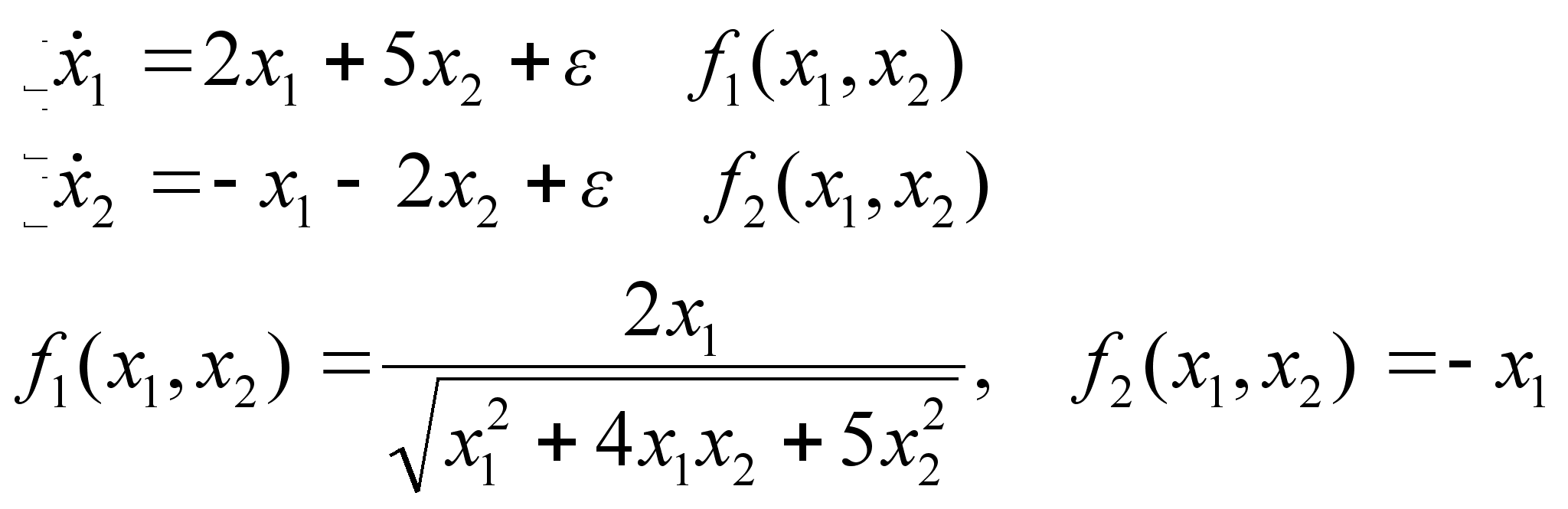
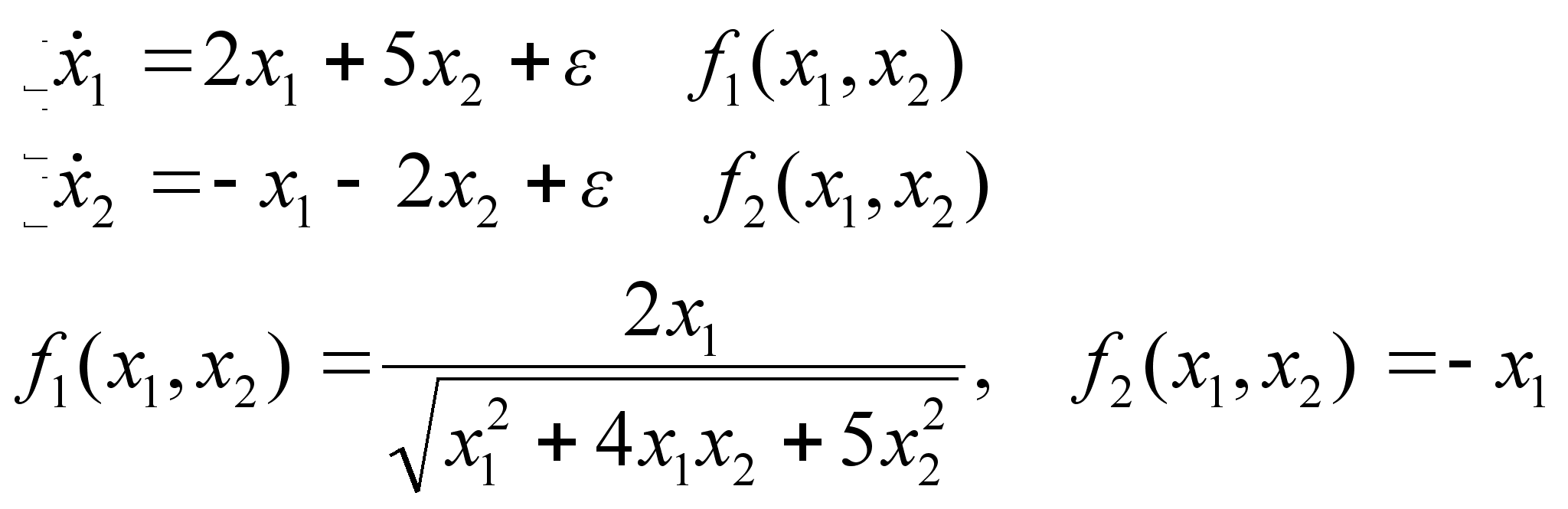
(1)
Сведем систему (1) к системе вида:
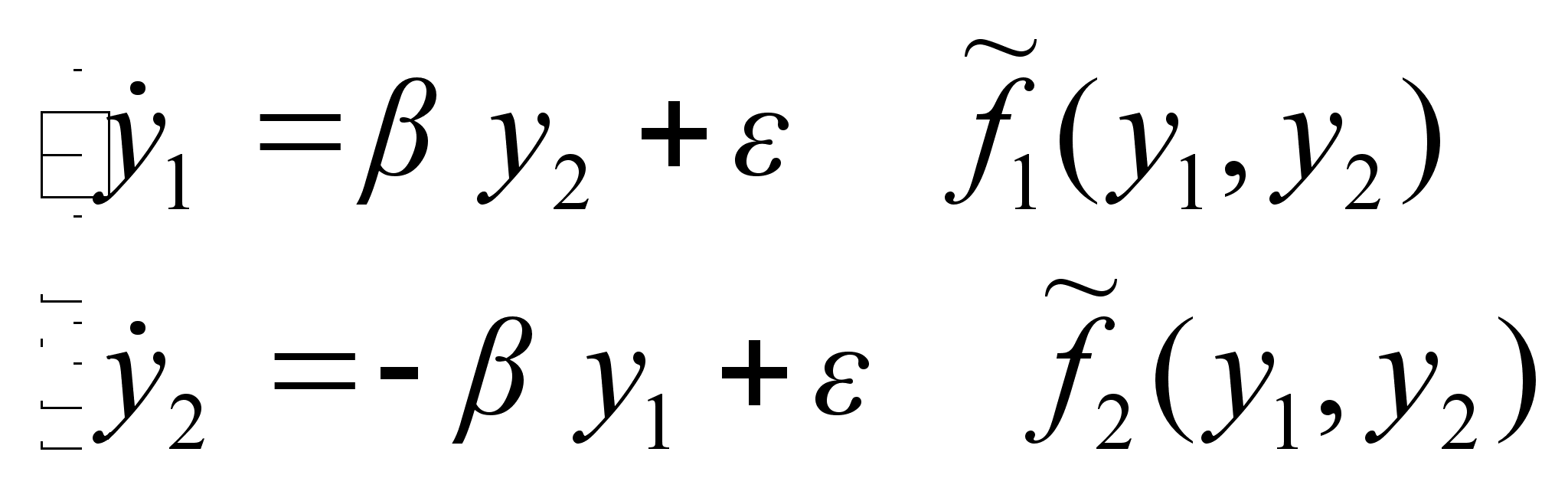
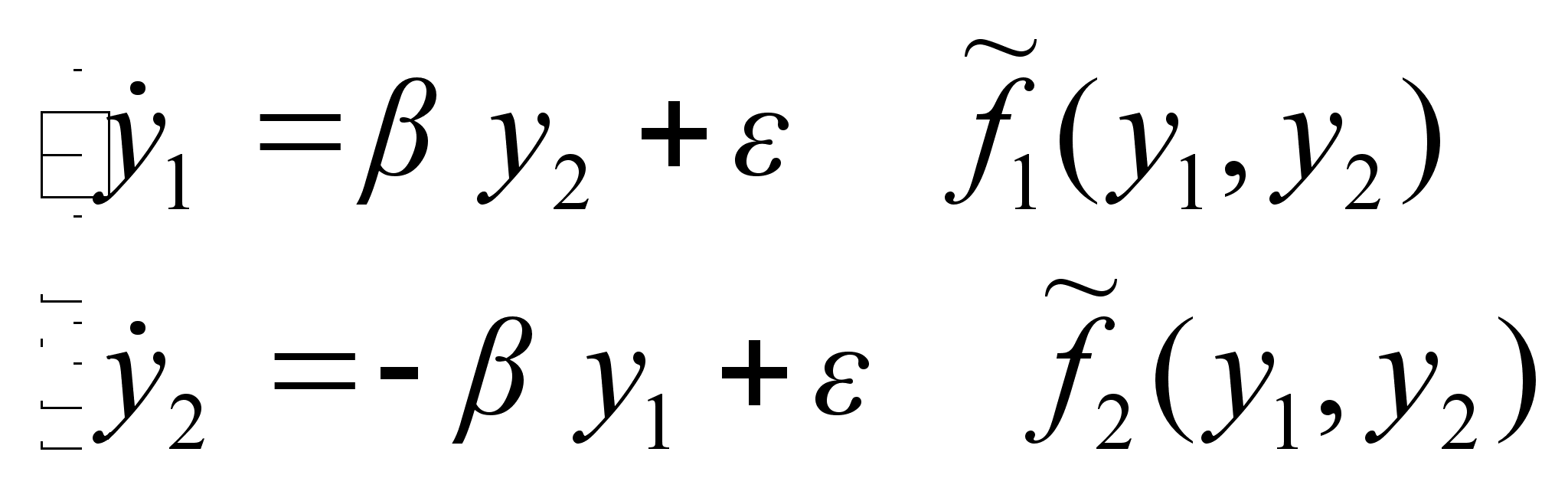
(2)
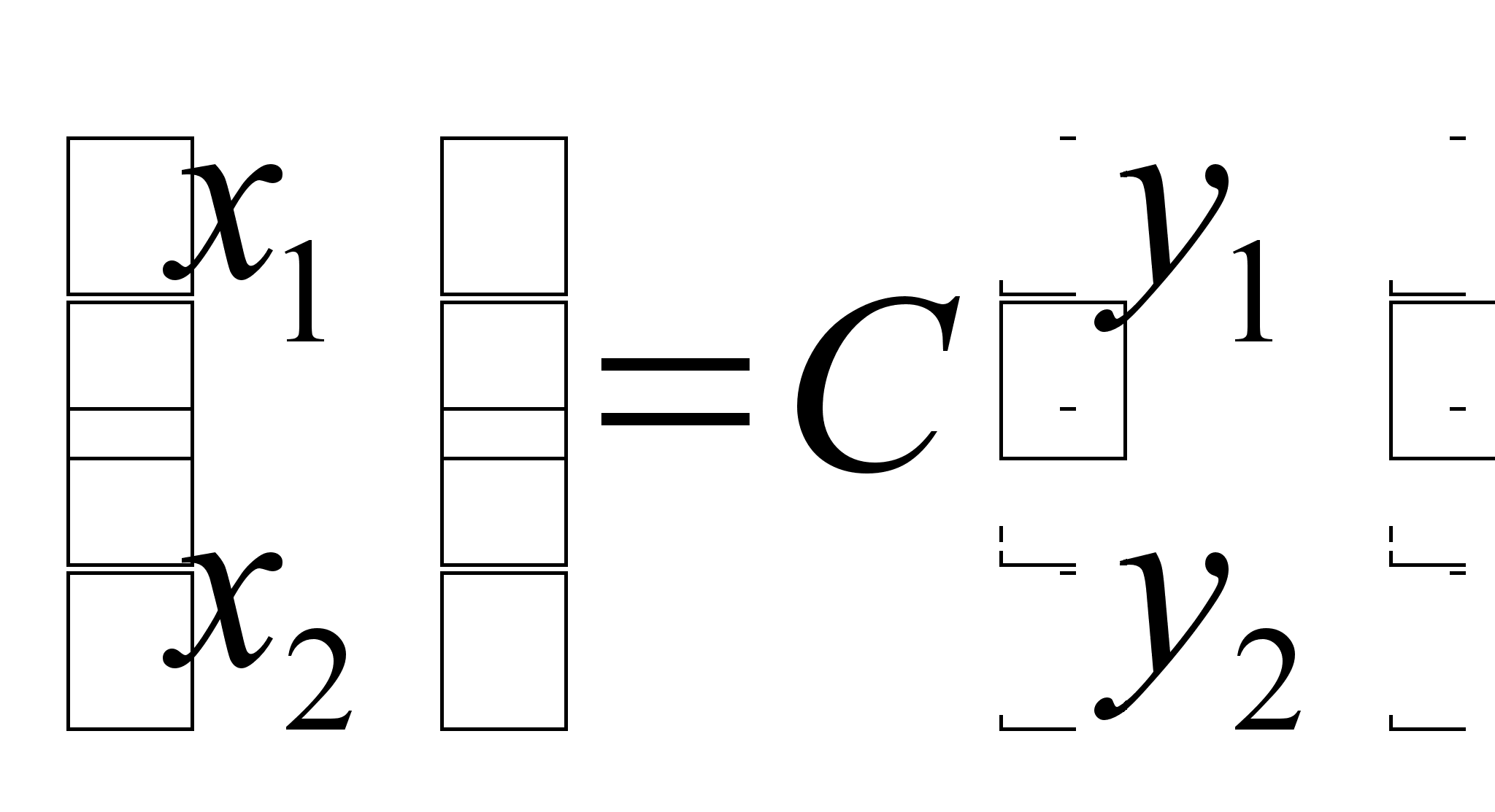
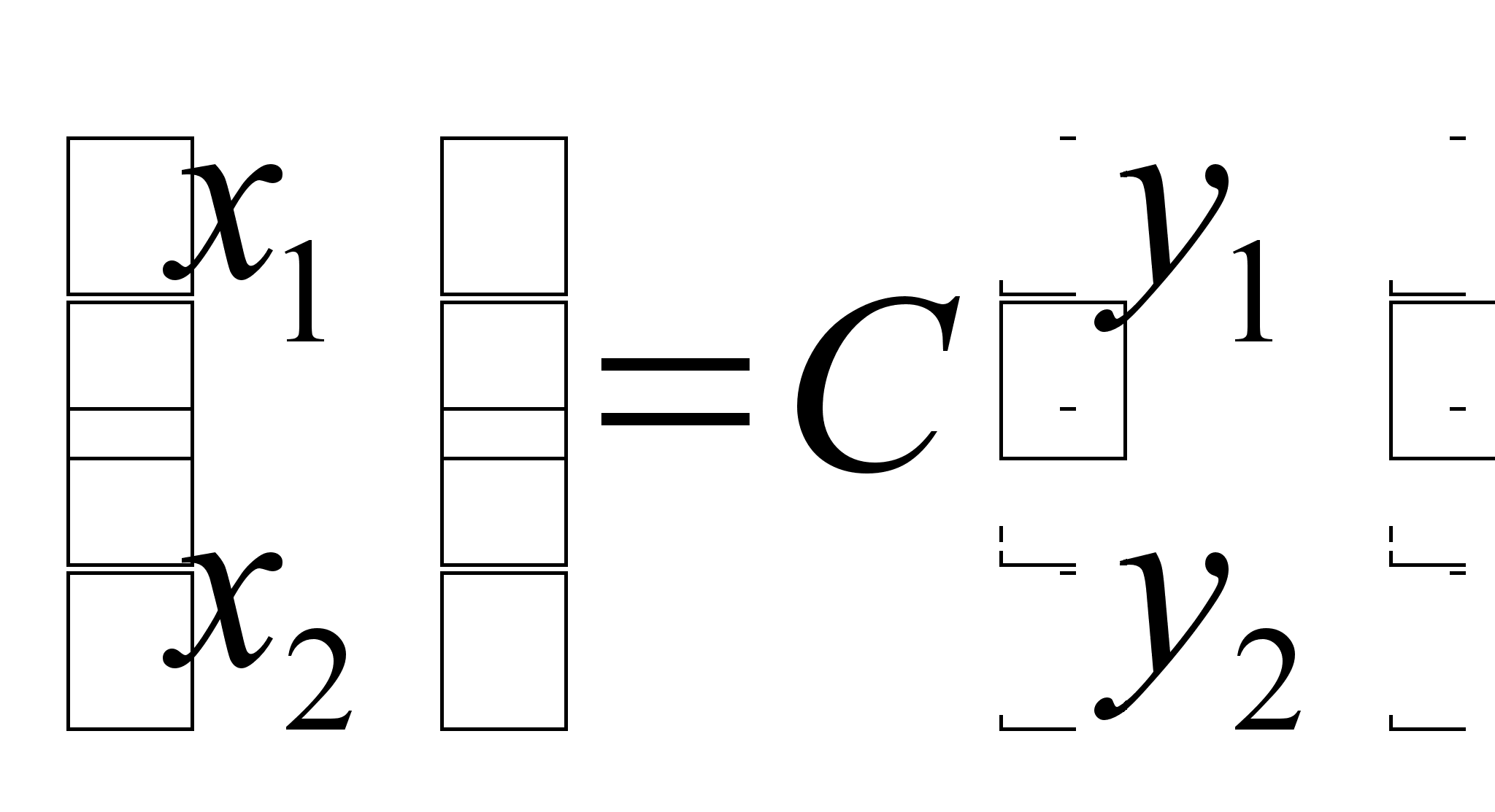
с помощью замены


![]()
![]()
Запишем систему (1) в виде

 (6 оценок, среднее: 4,67 из 5)
(6 оценок, среднее: 4,67 из 5)