Учебная работа № 1693. Нелинейные САУ

Учебная работа № 1693. Нелинейные САУ

Московский Государственный Технический Университет им. Н.Э. Баумана

Курсовая работа по курсу “Нелинейные САУ”

на

тему:

Применение метода частотных круговых диаграмм к исследованию устойчивости систем с логическими алгоритмами управления.

Выполнил: стт гр. АК481

Смык В.Л.

Реутов 1997 г.

Применение метода частотных круговых диаграмм к исследованию устойчивости систем с логическими алгоритмами управления.

На ранней стадии развития теории автоматического регулирования требование устойчивости работы системы было первым и обычно единственным и содержание большинства теоретических исследований сводилось к иследованию устойчивости.

“Термин “устойчивость” настолько выразителен, что он сам за себя говорит”,отмечают в начале изложения теории устойчивости Ж. Ла Салль и С. Лефшец [1]. Это вполне справедливо, но, несмотря на это, неточности и нелогичности можно встретить как раз не в математических, а в смысловых понятиях и терминах.

Устойчивостью любого явления в обиходе называю его способность достаточно длительно и с достаточной точностью сохронять те формы своего существования, при утрате которых явление перестает быть самим сабой. Однако не только в обиходе, но и в научной терминалогии устойчивым называют не явление, а систему, в корой оно наблюдается, хотя это не оправдывает логически. Устойчивы ли физические тела шар или куб? Такой вопрос будет иметь смысл, если речь идет о материале, из которого они сделаны. (Металлический шар

устойчив, шар из дыма нет.) Теорию управления интересует, однако, не эта прочнасная устойчивость. Подразумевается, что система управления как инженерная конструкция заведома устойчива, и в теории изучается устойчивость не самой системы, а ее состояний и функционирования. В одной и той же системе одни состояния или движения могут быть устойчивыми, а другие не устойчивыми. Более того, одно и то же жвижение может быть устойчивым относительно одной переменной и неустойцивым относительно другой это отмечал еще А.М. Ляпунов [2]. Вращение ротора турбины устойчиво по отношению к угловой скорости и неустойчиво относительно угла поворота вала. Движение ракеты устойчиво относительно траектории и неустойчиво по отношению к неподвижной системе координат. Поэтому нужно оговаривать, устойчивость какого состояния или движения в системе и относительно каких переменных изучается. Так же есть много методов для оценки самой устойчивости. Мы рассмотрим как можно оценить устойчивость системы с логическим алгоритмом управления методом круговых диаграмм.

Рассмотрим теоретическую часть и посмотрим что из себя представляет круговой критерий. Пусть дана система

.

x=Ax+b x , s =c’x, (1)

где x и s в общем случае векторы (и, следовательно, b и с прямоугольные матрицы), а матрица А не имеет собственных значений на линейной оси. Предположим , что для некоторого m, £m£

система (1), дополненая соотношением x=ms, асимптотически усойчива.

Для абсолютной экпоненциальной устойчивости системы (1) в классе М() нелинейностей x=j(s,t), удовлетворяющих условию

£ j ( s , t)/ s £ (2)

достаточно, чтобы при всех w,¥<w<+¥, выполнялось соотношение

Re{[1+ w ) ] [ 1 + W(j w )]}>0. (3)

Круговой критерий вытекает из квадратичного критерия для формы F(x,s)=(sx)(xs). Действительно, как было показано выше, форма F(jw,x) имеет вид

F(jw,x)=Re{[1+W(jw)][1+W(jw)]}|x|

Из этой формулы после сокращения на |x| следует (3).

В (3) ¹¥,¹+¥. Случай, когда либо =¥, либо =+¥ рассматривается аналогично.

Круговой критерий представляет собой распространение линейных частотных критериев устойчивости Найквиста, Михайлова и других на линейные системы с одним линейным или нелинейным, стационарным или нестационарным блоком. Он получается из (3), если вместо передаточной матрицы использовать частотную характеристику линейной части W(jw).

Обозначая комплексную переменную W(jw)=z, рассмотрим систему с одной нелинейностью, удовлетворяющей одному из следующих условий:

Re[(1+ z ) ( 1 + z)] £ 0, если ¹¥,¹+¥.(4)

Re[(1+ z)z] £ 0, если ¹¥,¹+¥.(5)

Re[z(1+z)] £ 0, если ¹¥,¹+¥.(6)

Пусть С() облость комплексной плоскости z, определяемая этими условиями. Граница В() области определяемая уравнениями получаемыми из (4)(6) заменой знаков неравенств равенствами. Для (4) получаем окружность, проходящую через точки 1/, 1/ сцентром на оси абсцисс, причем область С будет внутренностью этой окружности, если >0, т.е. если нелинейные характеристики лежат в 1 и 3 квадрантах, и ее внешностью, если сектор () захватывает два смежных квадранта. Если одна из границ сектора совпадает с осью абсцисс, т.е. если =0 или = 0 , то область С будет полуплоскостью, а ее граница вертикальной прямой, проходящей соответственно через 1/ или 1/. На рисунке 1 показаны границы в плоскости z для различного расположения секторов () в плоскости s,x. Там же изображены кривые W(jw), w>0 для неособого случая, расположенные так, что возможна абсолютная устойчивость. Однако только приемлимого расположения хаоактеристик W(jw) еще недостаточно для суждения об абсолютной устойчивости : кроме этого, нужно еще потребовать, чтобы линейная замкнутоя система была асимптотически устойчивой.

Круговой критерий обеспечивает также абсолютную устойчивость для системы с любым блоком, вход s и выход x которого удовлетворяют для всех t неравенству

( sx)(xs)³0 (7)

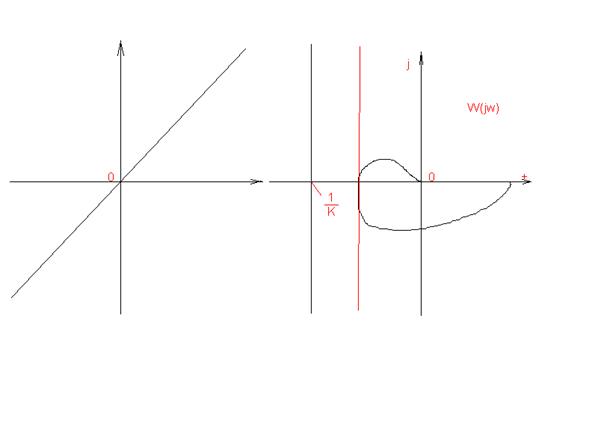
Рисунок 1, а.

Рассмотрим систему, приведенную на рис. 2.

А Х Y У (P) Z

()

Учебная работа № 1693. Нелинейные САУ