Учебная работа № 1646. О физической обоснованности некоторых идей в физике и космологии

Учебная работа № 1646. О физической обоснованности некоторых идей в физике и космологии

Йохан Керн

В статье обосновывается необходимость вернуться к независимости мысленных понятий и необходимость рассмотрения полной логической цепочки физического процесса в космологии и физике.

. Об ограничении свободы слова в физике и космологии

Ещё сто лет тому назад в физике и космологии каждый был волен фантазировать сколько хочет: главное, чтобы полученные выводы более или менее соответствовали наблюдаемой реальности. Время мыслилось как некоторая от нас независимая величина и могло иллюстрироваться равномерным вращением небесного тела или даже просто тиканием часов. Но вот с 1905 г. после написания Эйнштейном (18791955) своей эпохальной работы об электродинамике движущихся сред [1] стало ясно, что время зависит по крайней мере от скорости движения и перестало быть независимым от чего бы то ни было. Не только время длины и массы тел стали зависимыми от их скорости. Столь удивительных и непредставимых теоретических результатов, совершенно не увязывавшихся с существовавшим опытом, до него не получал никто. Это была истинная революция не только в физике, но и в мышлении.

Когдато и пространственные координаты мыслились как нечто абсолютное, не зависящее ни от каких физических процессов. Ведь и они были мысленными, а не действительными. Как на них могло чтото влиять?! Но после написания Эйнштейном его общей теории относительности стало ясно, что и независимость мысленных пространственных координат становится делом прошлого. Теория относительности вторглась даже в свободу мышления. Конечно, в быту всё ещё можно петь “Die Gedanken sind frei” (мысли свободны, мысль не арестуешь), но в физике и космологии никак нельзя отклоняться от правил теории относительности. Автор известного в Германии учебника физики пишет: “In der modernen Physik geht nichts mehr ohne die Relativitдtstheorie. ” [2] (“В современной физике ничто уже не идёт без теории относительности”). Это немного похоже на цензуру и, соответственно, на диктатуру теории относительности. Но, наверное, это только говорит о необходимости считаться с реальностью. Свобода повзрослевшей науки, также и как свобода повзрослевших детей, становится в определённом смысле ограниченной. Такова жизнь. Для ободрения тех, кого это разочаровывает, заметим, что Аристотель, отец демократии, считал, что наилучшая форма правления – диктатура. При разумном диктаторе. Порадуемся тому, что Эйнштейн явно относится к разумнейшим личностям, а его теория относительности – к творениям разума.

Нечто подобное наблюдается и в космологии. После того, как Эдвин Хабл (Hubble, 18891953) в 1929 г. обнаружил разбегание галактик, возникла теория “большого взрыва”, произошедшего по теории Эйнштейна в момент времени t = 0. После этого знаменательного события уже нельзя заниматься вопросом: “А что же было до “большого взрыва”? Грамотные редакторы научных и популярных журналов саркастически ответят вам: “А ничего не было!” и отклонят вашу работу, даже не пытаясь отправить её к рецензентам. И здесь цензура, и здесь правление догмы? Но, может быть, и это совершенно правильно? Ведь французская Академия Наук ещё задолго до появления теории относительности тоже прекратила рассмотрение непрерывно поступавших проектов “вечных двигателей”. Некоторым иначе не втолкуешь, что “вечные двигатели” невозможны.

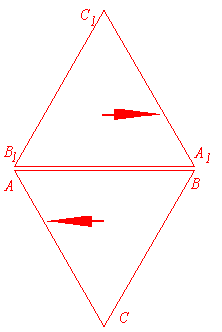
Рис. 1. Начальная позиция равносторонних треугольников. Стороны AB и B1A1 параллельны друг к другу и соприкасаются (отчётливо показанная щель между ними на самом деле отсутствует). В начальном положении треугольники могут перемещаться в направлениях, показанных стрелками. AB = B1A1.

1. Об одном мысленном эксперименте, который, казалось бы, противоречит теории относительности

Разумеется, этот эксперимент мы делаем только с целью углубить наше понимание теории относительности. Эксперимент очень простой, но, как мы убедимся, он довольно поучительный. Представим себе два равных по величине раносторонних плоских треугольника ABC и A1B1C1. Плоскости треугольников находятся на расстоянии R от общей (неподвижной) оси вращения, вокруг которой они могут вращаться независимо друг от друга. При совпадении плоскостей треугольников прямые AB и B1 A1 параллельны, (почти) соприкасаются друг с другом, а точки C и C 1 находятся друг против друга (рис. 1). Направление возможного движения совпадает с направлением прямых AB и B1 A1. Радиус R представим очень большим (астрономических размеров).

Снабдим теперь все угловые точки треугольников одинаковыми зараннее синхронизированными часами, а треугольник ABC ещё и наблюдателями с фотоаппаратами (наблюдателей будем обозначать одинаково с обозначением точек, в которых они находятся) и начнём вращать оба треугольника с одинаковым ускорением в противоположные стороны. (Направление движения показано на рис. 1 стрелками.) При достижении определённой зараннее договорённой линейной скорости v/2 ускорение прекращается и оба треугольника вращаются далее с одинаковой угловой скоростью. Когданибудь, по истечении весьма длительного промежутка времени прямая AB снова совпадёт с прямой B1 A1. В этот момент все наблюдатели делают снимки обоих треугольников (наблюдатель в точке C делает снимок в тот момент, когда видит прямую AB снова совпадающей с прямой B1 A1). Снимки наблюдателей A, B и C показаны на рис. 2, 3 и 4. С точки зрения этих наблюдателей треугольник A1B1C1 является движущейся системой координат, перемещающейся с относительной скоростью v. (Для любого достаточно короткого промежутка времени движение треугольников можно считать прямолинейным)

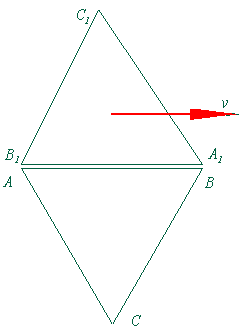
Рис.2.

На рис. 2 находится снимок наблюдателя C. На его снимке совпадают прямые AB с B1A1, показания часов в точках A,B, B1 и A1 совпадают. (Это естественно. Наши треугольники в начале путешествия получили синхронизированные часы и двигались в любой момент с одинаковой скоростью, но только в различном направлении. Естественно принять, что течение времени и изменение длин не зависят от направления движения). Показание часов в точке C1 отстаёт и сама точка C1 также смещена назад. Это оттого, что свет из точки C1 идёт дольше, чем из точек A, B, B1 и A1.

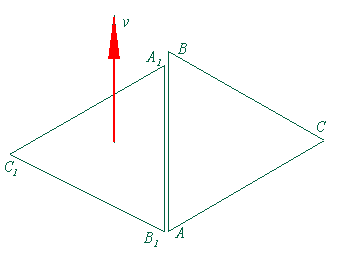
Рис.3.

На снимке из точки A (рис. 3) прямая B1 A1 оказывается короче прямой AB, часы в точке A1 отстают от часов в точке A. Но из снимка на рис. 2 мы уже знаем, что нам это только кажется: пока свет из точки A1 шёл к точке A, точка A1 дошла до точки B. Обозначим длину AB = L, а кажущуюся длину B1 A1 = L1. Тогда мы получим

L1= c t* и (L L1) = vt*,

где t* время, необходимое свету, чтобы пройти расстояние от точки A1 до A, а с – скорость света. Из этих двух равенств мы можем определить:

t* = L/( c + v) и L1 = L c /( c + v) (1)

(Чтобы нам в наших расчётах не учитывать эффекты изза движения света в разных системах отсчёта, мы можем представить, что напротив точки A1 на прямой AВ находится зеркало, отражающее свет от точки A1 в сторону точки A. Так как прямые AB и B1A1 практически соприкасаются, то необходимый дополнтельный интервал времени для хода светового луча равен 0. В наших расчётах от этого ничего не меняется.

Этот же приём может быть применён и в следующих расчётах к нашему снимку 4.)

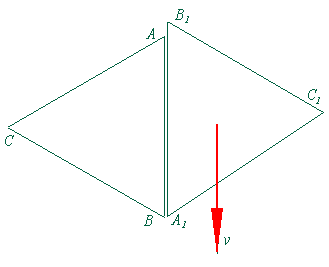
Рис.4.

На снимке из точки B (рис. 4) прямая A1 B1 оказывается длиннее прямой BA, часы в точке B1 отстают от часов в точке B. Но из снимка на рис. 2 мы опятьтаки знаем, что нам это только кажется: пока свет из точки B1 шёл к точке B, точка B1 дошла до точки A. Обозначим кажущуюся длину A1B1 = L2. Тогда мы получим

L2= c t* * и (L2 L) = vt**,

где t** время, необходимое свету, чтобы пройти расстояние от точки B1 до точки В. Из этих двух равенств мы определяем:

t** = L/( c v) и L2 = L c /( c v) (2)

Полученные выражения (1) и (2) для длины A1B1 чемто напоминают выражения, получаемые в теории относительности, но именно только напоминают. Странно прежде всего то, что у нас, в зависимости от точки наблюдения, получены 3 различных значения длины для A1B1, в то время как в теории относительности получено только укорочение движущегося отрезка, расположенного вдоль направления скорости движения, причём не кажущееся, а действительное. Разумеется, мы действовали не по Эйнштейну, но ведь длина отрезка A1B1 в движущейся системе координат должна быть одна и та же, независимо от точки наблюдения, и не кажущаяся, а действительная.

Посмотримка внимательно, как это делал сам Эйнштейн, и не по учебнику, а по первоисточнику.

2. Конспект доказательства наличия своеобразных эффектов (сокращения длины отрезков, интервалов времени и пр.) в движущейся системе отсчёта по статье Эйнштейна [1] (с комментариями)

Сразу после названия “К электродинамике подвижных тел” [1] следует нечто вроде введения, в котором Эйнштейн, в частности, упоминает потерпевшие неудачу эксперименты с целью определить движение Земли относительно “светоносного эфира”. Кроме того, высказывается намерение обосновать предположение, что свет в пустом пространстве перемещается с постоянной скоростью, не зависящей от скорости источников света.

§1 посвящён определению понятия одновремённости. Эйнштейн предлагает считать одинаковые часы идущими синхронно, если время прохождения светового луча между часами в одну сторону равно времени прохождения в другую сторону. Кроме того, скорость света, определяемая как отношение двойного расстояния между двумя точками ко времени прохождения света от одной точки к другой и обратно, объявляется универсальной постоянной.

§2 посвящён относительности длин и времён (отрезков времени). В нём указывается, что длина подвижного стержня, измеренного в подвижной системе координат, не будет равна длине стержня в неподвижной системе координат. Показывается, что синхронные часы на подвижном стержне не являются синхронными при измерении в соответствии с §1 из неподвижной системы координат.

§3 посвящён теории трансформации времени и координат подвижной системы координат относительно неподвижной. (По названию этого параграфа можно было бы заподозрить, что Эйнштейн задумал сделать нечто такое, что физику делать непозволительно, так как “трансформация времени и координат” может означать сжатие или растяжение осей времени и пространства. Но мы, конечно, такого не думаем, во всём надо знать меру. Мы исходим из того, что если Эйнштейн сделает подобное преобразование координат, то он затем сделает и обратное преобразование при возвращении в реальную систему координат с нормальными недеформированными осями времени и пространства) В этом параграфе Эйнштейн, ставя условием, что скорость света и в подвижной системе координат должна быть равна c, находит такое преобразование неподвижных координат, что сферический фронт световой волны в неподвижной системе координат и в подвижной выглядят сферическими. (Здесь, наверное, следовало бы добавить, выглядят сферическими с точки зрения математика, потому что для математика сферой является всё, что можно выразить формулой

x2 + y2 + z2 = R2. (3)

Для математика элипсоид в одной системе координат можно соответствущим преобразованием (растяжением или сжатием) координат превратить в другой системе координат в сферу. Подобное может оказаться удобным для преобразования подинтегральной функции с целью облегчения взятия интеграла или других надобностей. В этой ситуации после решения определённой задачи надо вернуться в реальную нетрансформированную, т.е. в неискажённую систему координат. С точки зрения физика сфера только тогда сфера, если она сфера в реальной, т.е. в неискажённой системе координат.)

Другими словами, в §3 для выполнения указанного постулированного условия Эйнштейном в подвижной системе координат введена трансформация оси, параллельной направлению движения. В связи с этим, для сохранения сферической (в смысле равенства (3)) формы светового фронта при величине его скорости равной c, автоматически трансформировалась и ось времени. Причём коэффициент трансформации обеих осей

1/[1(v/c)2]0,5

зависит от величины относительной скорости v подвижной системы координат. Поэтому с изменением скорости v в этой (трансформированной) системе координат автоматически происходит соответствующее изменение отрезков длины вдоль оси движения и интервалов времени.

Свой §4 Эйнштейн посвятил “физическому значению (толкованию) полученных уравнений в отношении твёрдых тел и подвижных часов”. (По названию этого параграфа ктонибудь мог бы подумать, что Эйнштейн уже собирается собирать лавры! Но мы, конечно, такого не подозреваем. Мы отлично помним, что Эйнштейн был не только серьёзным исследователем, но и гением в области физики.) В самом начале этого параграфа он подтверждает, что сфера, определяемая в подвижной системе координат формулой (3), в неподвижной будет элипсоидом. Он ясно представляет, что в полученной им подвижной системе координат “время” будет протекать медленнее, что он находит весьма “своеобразным следствием”. Заканчивает он этот параграф утверждением, что часы на земном экваторе будут идти несколько медленне, чем такие же часы на полюсе. (Т.е. район экватора, по его мнению, достаточно точно представляет собой инерциальную систему. Мы можем быть уверены, что наш собственный мысленный эксперимент, описанный в прошлом разделе, не вызвал бы у него нареканий в смысле достаточного приближения к инерциальной системе отсчёта). Это его утверждение показывает, что он реальную систему, район экватора, сравнивает со своей трансформированной подвижной системой координат. Не должно ли это означать, что он уже действительно пожинает лавры, другими словами, что он забыл, что в его трансформированной подвижной системе координат ось времени и одна из пространственных

Учебная работа № 1646. О физической обоснованности некоторых идей в физике и космологии