Учебная работа № 1596. Операторные уравнения

(6 оценок, среднее: 4,67 из 5)

Загрузка...

Учебная работа № 1596. Операторные уравнения

Выпускная квалификационная работа

Выполнила студентка V курса математического факультета Кощеева Анна Сергеевна

Вятский Государственный Гуманитарный университет (ВятГГУ)

Киров 2005

Функциональный анализ – мощное средство для решения математический задач, возникающих в реальных ситуациях, он имеет множество приложений в различных областях математики, его методы проникают в смежные технические дисциплины.

Многие задачи математической физики, теории упругости, гидродинамики сводятся к отысканию решения дифференциального линейного уравнения, что, в свою очередь, приводит к задаче отыскания решения уравнения Аx = y с линейным оператором А. В данной работе рассмотрены два метода решения операторных уравнений.

Цель данной работы: рассмотреть основы теории линейных операторов и методы решения операторных уравнений – метод малого параметра и метод продолжения по параметру, показать применение этих методов к решению задач.

Изучив имеющийся материал по данной теме, я поставила перед собой следующие задачи:

раскрыть некоторые основы теории линейных операторов, необходимые для освоения методов решения операторных уравнений;

проиллюстрировать на конкретных примерах способы решения операторных уравнений и дать пояснения по ходу решения конкретных задач.

Так как выделение из функционального анализа его прикладной части, содержащей конструктивные методы получения решений задач, преследует методическую цель – сделать эти методы доступнее тем, кто занимается приложениями математики. Поэтому данная работа разделена на две главы, в первой содержатся необходимые теоретические обоснования способов решения операторных уравнений и суть обоих методов, а во второй – решения конкретных задач.

Глава 1. Операторные уравнения

§1.Определение линейного оператора

Пусть X и Y – линейные пространства, оба вещественные или оба комплексные.

Оператор А: X → Y с областью определения D(А) называется линейным, если

А(λ1×1 + λ2×2) = λ1А(x1) + λ2А(x2)

для любых x1,x2 Î D и любых скаляров λ1 и λ2.

Пусть X и Y – нормированные пространства и А: X → Y, где А – линейный оператор, всюду заданный в X (т.е. D(А) = X).

Оператор А называется непрерывным в точке x0 Î X, если Аx → Аx0 при x → x0. Но судить о непрерывности линейного оператора в различных точках x0 Î X можно по непрерывности его в нуле пространства X.

Теорема 1. Пусть линейный оператор А всюду задан в банаховом пространстве X и со значениями в банаховом пространстве Y непрерывен в точке 0 Î X; тогда А непрерывен в любой точке x0 Î X.

Доказательство. Рассмотрим равенство Аx – Аx0 = А (x – x0). Если x → x0, то z = x – x0 → 0. По непрерывности в нуле Аz → 0, но тогда Аx – Аx0 → 0, что и требовалось доказать.

Линейный оператор А называется непрерывным, если он непрерывен в точке x = 0.

Пусть S1(0) – замкнутый шар ||x|| ≤ 1 в банаховом пространстве X.

Будем называть линейный оператор А: X → Y ограниченным, если он ограничен на единичным шаре S1(0), т.е. если ограничено множество

{ ||Аx||, ||x|| ≤ 1}.

Согласно определению, если А ограничен, то существует постоянная с > 0 такая, что для любых x с ||x|| ≤ 1 справедливо неравенство

||Аx|| ≤ с (1)

Теорема 2. А ограничен тогда и только тогда, когда справедлива оценка

||Аx|| ≤ с ||x|| (2)

для любых x Î X, где с – постоянная.

Теорема 3. Пусть А: X → Y, А – линейный оператор, X, Y – банаховы пространства. Для того чтобы А был непрерывным, необходимо и достаточно, чтобы он был ограниченным.

§2. Норма линейного оператора

В линейном пространстве непрерывных линейных операторов зададим норму следующим образом:

. (1)

Поясним, почему существует конечное число ||А||, определяемое для любого ограниченного оператора равенством (1). Так как А – ограничен, то множество

ограничено сверху. По теореме о верхней грани существует .

Из свойства sup M следует, что ||Аx|| ≤ ||А|| для всех x Î S1(0). Отсюда

||Аx|| ≤ ||А|| ||x||, (2)

справедливое для всех x Î X, включая x = 0. таким образом, ||А|| является наименьшей из констант в неравенстве ||Аx|| ≤ ||А||, и, значит, оценка (2) является наилучшей.

Пространство нормированных непрерывных линейных операторов, действующих из X в Y, будем обозначать L(X, Y).

§3.Обратные операторы

Системы линейных алгебраических уравнений, интегральные уравнения, а также различные задачи для обыкновенных дифференциальных уравнений и уравнений с производными часто могут быть записаны в виде линейного уравнения

Если существует обратный оператор , то решение задачи записывается в явном виде:

Важное значение приобретает теперь выявление условий, при выполнении которых обратный оператор существует и обладает теми или иными свойствами.

Пусть задан линейный оператор: А: X → Y, где X,Y – линейные пространства, причем его область определения D(A)X, а область значений R(A)Y.

Введем множество множество нулей оператора А. заметим, что N(A) не пусто, так как 0 Î N(A)

Теорема 4. Оператор А переводит D (А) в R (А) взаимно однозначно тогда и только тогда, когда N(A)=, (т.е. множество А нулей состоит только из элемента 0)

Теорема 5. Оператор А1 существует и ограничен на R(A) тогда и только тогда, когда для некоторой постоянной m>0 и любого x Î D(A) выполняется неравенство

. (1)

Введем теперь следующее важное понятие.

Будем говорить, что линейный оператор А: X → Y непрерывно обратим, если R(A)=Y , оператор обратим и A1 Î L(Y, X), (т.е. ограничен).

Обращаясь к теореме 5, мы сможем сформулировать следующее утверждение.

Теорема 6. Оператор А непрерывно обратим тогда и только тогда, когда R(A)=Y и для некоторой постоянной m>0 и для всех выполняется неравенство (1).

В случае определенного и ограниченного на всем множестве оператора A Î L(X,Y) имеется теорема Банаха об обратном операторе.

Теорема 7. Если А – ограниченный линейный оператор, отображающий взаимно однозначно банахово пространство X на банахово пространство Y, то обратный оператор А1 ограничен.

Иными словами, если А Î L(X,Y), где X и Y банаховы, R(A)=Y и А обратим, то А непрерывно обратим.

Взглянем на понятие непрерывно обратимого оператора с точки зрения разрешимости линейного уравнения

Ax = y (2)

Если А непрерывно обратим, то уравнение это имеет единственное решение x = A1y для любой правой части у. Если при этом (решение того же уравнения с правой частью ), то . Это означает, что малое изменение правой части y влечет малое изменение решения, или, как принято говорить, задача (2) корректно разрешима.

Пусть А Î L(X,Y). Оператор U Î L(X,Y) будем называть правым обратным к А, если AU = Iy. Оператор V Î L(X,Y) будем называть левым обратным к А, если VA = Ix.

Здесь через Iy (Ix) обозначен тождественный оператор в пространстве Y (X). Ниже для правого обратного к А используем обозначение Аr–1, а для левого – АL–1.

Лемма 1. Если существует правый обратный Аr–1 к А, то уравнение (2) имеет решение

x = Аr–1 y

Если существует левый обратный оператор к А, то уравнение (2) может иметь не более одного решения.

Доказательство.

А(Аr–1 y) = (А Аr–1)y = y,

т.е. x = Аr–1 y обращает (2) в тождество и, значит, является решением.

Далее, пусть существует АL–1. рассмотрим N(A). Пусть x Î N(A), тогда Аx = 0. применим к этому равенству оператор АL–1, тогда АL–1Аx = 0, откуда x = 0. итак, всякое x Î N(A) оказывается равным 0. Значит, N(A) = {0} и, по теореме 4, А взаимно однозначен, т.е. для уравнения (2) справедлива теорема единственности. Что и требовалось доказать.

Пусть X – банахово пространство. Рассмотрим банахово пространство L(X) – пространство линейных, ограниченных и заданных на всем множестве операторов. Пусть I – тождественный оператор в L(X). Очевидно, что I непрерывно обратим. Ниже доказывается, что вместе с I непрерывно обратимы все операторы единичного шара в L(X), т.е. все такие А, для которых справедливо неравенство .

Для краткости положим C = I – A. Ниже мы будем ссылаться на признак Вейерштрасса: пусть X – банахово пространство, тогда всякий абсолютно сходящийся в X ряд сходится.

Теорема 8. Пусть и ; тогда оператор I – C непрерывно обратим. При этом справедливы оценки

(1)

(2)

Доказательство. Рассмотрим в L(X) ряд

I+C+C2+C3+… (3)

Так как , то ряд (3) оценивается сходящимся числовым рядом – геометрической прогрессией

По признаку Вейерштрасса ряд (3) сходится равномерно, т.е.

Где S – сумма ряда (3). Далее простой проверкой убеждаемся, что

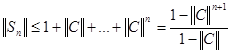
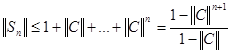
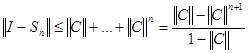
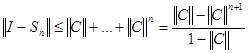
Но при этом (ибо и ), а . Поэтому, в пределе имеем равенства (I – C)S = I и S(I – C) = I. По лемме 1 отсюда заключаем, что I – C непрерывно обратим и S=(I – C)1. Далее,

Переходя в этих неравенствах к пределу при , получаем оценки (1) и (2). Теорема доказана.

Теперь рассмотрим более общий случай пространства L(X,Y). Пусть А Î L(X,Y) непрерывно обратим.

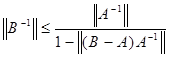
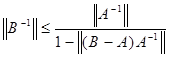
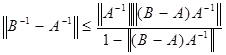
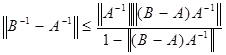
Теорема 9. Пусть A, B Î L(X,Y), А непрерывно обратим и выполнено неравенство . Тогда B непрерывно обратим и справедливы оценки

, .

§4. Абстрактные функции

Пусть S – некоторое множество на числовой оси или в комплексной плоскости, а X – нормированное пространство.

Рассмотрим функцию x() с областью определения S и с областью значений в X. Такие функции принято называть абстрактными функциями числовой переменной или векторными функциями числовой переменной, поскольку элементы линейного (иначе – векторного) пространства мы называем также векторами. На абстрактные функции числовой переменной переносятся многие понятия и факты математического анализа. Далее рассмотрим сведения о пределах и непрерывности таких функций, о разложении в степенные ряды, а также понятие аналитической абстрактной функции.

Пусть x() определена в окрестности точки 0, за исключением, быть может, самой точки 0. Элемент а Î X будем называть пределом функции x() при →0 и записывать

при →0,

если при →0.

Степенные ряды – это специальный случай рядов в нормированном пространстве, когда члены ряда зависят от параметра.

Рассмотрим в нормированном пространстве X ряд вида , где xк Î X, а – вещественное или комплексное переменное. Поскольку можно ввести новую переменную –0 = , то в дальнейшем мы полагаем 0 = 0 и рассматриваем степенные ряды вида