Учебная работа № 1528. Шпоры по вышке

Учебная работа № 1528. Шпоры по вышке

1. Матрицы. Линейные операции над ними и их свойства.

Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины.

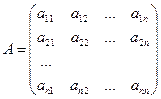
Матрицы равны между собой, если равны все их соответствующие элементы.

Матрица, у которой число строк и столбцов равно – называется квадратной .

Матрица, все элементы которой, кроме элементов главной диагонали равны нулю, называется диагональной .

Диагональная матрица, у которой все элементы главной диагонали равны 1, называется единичной . Обозначается буквой Е.

Матрица, у которой все элементы по одну сторону от главной диагонали равны нулю, называется треугольной .

Матрица, у которой все элементы равны нулю, называется нулевой .

1.

2.

3.

4.

5.

6.

7.

8.

2. Умножение матриц. Транспонирование. Свойства.

Операция умножения возможна, если количество столбцов первой матрицы равно количеству строк другой матрицы.

где

1.

2.

3.

4.

Матрица, полученная заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной , к данной.

1.

2.

3. Определители матриц. Свойства определителей. Миноры и алгебраические дополнения.

1.

2.

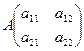
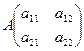
3.

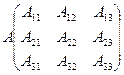
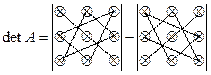
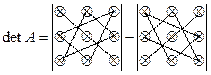
Для нахождения определителя более высокого порядка, матрицу приводят к треугольному виду и считают произведение элементов на главной диагонали.

Свойства:

1. Определитель не изменится, если его строки заменить столбцами, и наоборот.

2. При перестановке двух параллельных рядов определитель меняет знак.

3. Определитель, имеющий два одинаковых или пропорциональных ряда, равен нулю.

4. Общий множитель элементов можно вынести за знак определителя.

5. Если элементы какоголибо ряда представляют собой сумму элементов, то определитель может быть разложен на сумму двух соответствующих определителей.

6. Определитель не изменится, если прибавим ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и тоже число.

7. Определитель равен сумме элементов, умноженных на соответствующее им алгебраическое дополнение.

8. Сумма произведения элементов одного ряда на алгебраические дополнения параллельного ряда равна нулю.

4. Разложение определителя по элементам ряда. Теорема замещения.

Определитель равен сумме произведений элементов на соответствующее им алгебраическое дополнение.

Берем любые Nчисел и умножим на алгебраическое дополнение какойлибо строки.

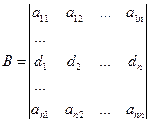
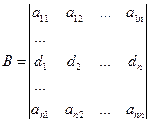
5. Обратная матрица. Достаточное условие существования обратной матрицы.

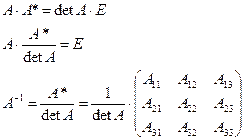
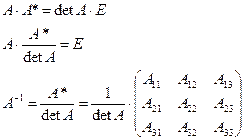
1.

2.

3.

Для того чтобы матрица имела обратную достаточно того, чтобы она была невырождена.

6. Элементарные преобразования матриц. Ранг матрицы. Вычисление ранга матрицы.

1. Перестановка местами 2 параллельных рядов матрицы.

2. Умножение элементов ряда матрицы на число отличное от нуля, отличное от нуля.

3. Прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и тоже число.

Из элементов стоящих на пересечении выделенных строк и столбцов, составим определитель kого порядка. Наибольший из порядков таких миноров называется рангом матрицы.

7. Решение линейных уравнений. Решение невырожденых систем.

Метод Гаусса.

Сначала следует привести систему к треугольному (ступенчатому) виду, а затем ступенчато решить.

Формула Крамера.

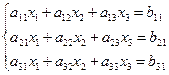
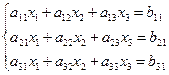
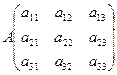
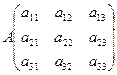
Подсчитать определитель матрицы А.

Затем матрицей B заменить первый столбец матрицы А, подсчитать определитель и разделить его на detA, так мы получим x₁ . То же самое проделать со 2ым и 3им столбцом.

8. Решение произвольных систем. Теорема КронекераКапелли.

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.

Найти какойлибо базисный минор порядка r. Взять r уравнений, из которых составлен базисный минор. Неизвестные, коэффициенты которых входят в базисный минор, называются главными и остаются слева, а остальные называются свободными и переносятся в правую часть уравнения. Найдя главные через свободные, получим общее решение системы.

9. Однородные система уравнений. Фундаментальная система решений.

Система однородных уравнений всегда имеет нулевое решение. Если ранг матрицы меньше числа неизвестных, то система имеет бесчисленное множество решений. Для того, чтобы система имела ненулевые решения, необходимо, чтобы ее определитель был равен нулю.

10. Линейные пространства. Линейная зависимость и независимость системы векторов. Размерность и базис линейного пространства.

Рассмотрим непустое множество элементов, которые будем обозначать через x, y, z, … и множество действительных чисел. На этом множестве введем две операции (сложение и умножение). Пусть эти две операции подчиняются аксиомам:

1.

2.

3.

4.

5.

6.

7.

8.

V; x, y, z, … V

Множество V с двумя операциями, удовлетворяющее аксиомам называется линейным пространством.

Элементы линейного пространства называются векторами, обозначаются , , . Существует единственный нулевой элемент, для каждого элемента существует единственный противоположный.

Линейная зависимость и независимость системы векторов. Пусть имеется n векторов.

Составим линейную комбинацию:

, если система n векторов – линейнозависима.

Если среди n векторов какието kлинейнозависимы, то вся система векторов является линейнозависимой.

Если система n векторов линейнонезависима, то любая часть из этих векторов будет тоже линейнонезависимой.

Размерность и базис линейного пространства. Пусть система n векторов линейнонезависима, а любая система n+1 векторов – линейнозависима, тогда число n называют размерностью пространства. dimV=n

Система этих n линейнонезависимых векторов называется базисом линейного пространства. Рассмотрим систему n+1 векторов.

Такое представление называется разложение по базису, а числа называют координатами вектора.

Разложение любого вектора в выбранном базисе единственно.

11. Матрица перехода от базиса к базису. Преобразование координат вектора при переходе к новому базису.

n – мерное пространство.

V_n – базис, состоящий из n векторов.

В пространстве есть базисы

Введем матрицу перехода от к .

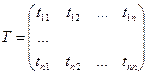
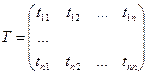
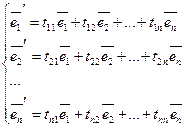
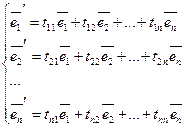
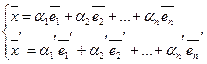
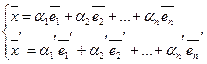
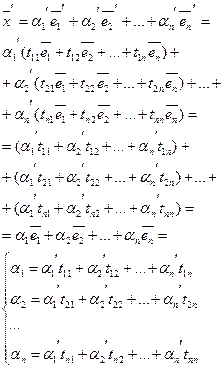
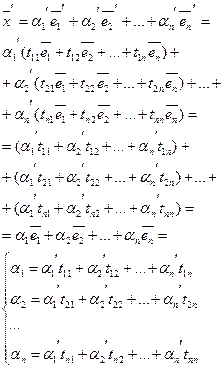
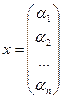
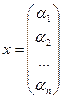
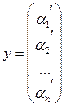
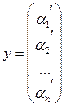
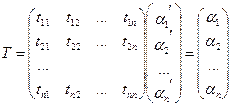
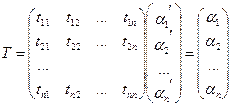
12. Евклидово пространство. Длина вектора. Угол между векторами.

Рассмотрим линейное пространство V, в котором уже есть 2 операции (сложение и умножение). В этом пространстве введем еще одну операцию. Она будет удовлетворять следующим аксиомам.

1.

2.

3.

4.

Указанная операция называется скалярным произведением векторов. N – мерное линейное пространство с введенной операцией скалярного произведения, называется Евклидовым пространством .

Длиной вектора называется арифметическое значение квадратного корня и скалярного квадрата.

Длина вектора удовлетворяет следующим условиям:

1. , если

2.

3. неравенство КошиБуня

4. неравенство треугольника

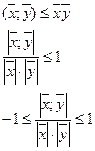
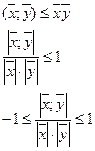
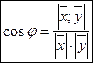
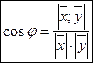
13.Скалярное произведение векторов и его свойства.

Скалярным произведением двух ненулевых векторов называется число, равное произведению этих векторов на косинус угла между ними.

1.

2.

3.

4.

14. Векторное произведение векторов и его свойства.

Три некомпланарных вектора образуют правую тройку если с конца третьего поворот от первого вектора ко второму совершается против часовой стрелки. Если по часовой – то левую .

Векторным произведением вектора на вектор называется вектор , который:

1. Перпендикулярен векторам и .

2. Имеет длину, численно равную площади параллелограмма, образованного на векторах и .

, где

3. Векторы, и образуют правую тройку векторов.

Свойства:

1.

2.

3.

4.

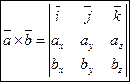
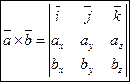
15. Смешанное произведение векторов и его свойства.

Смешанное произведение записывают в виде: .

Смысл смешенного произведения: сначала два вектора векторно перемножают, а затем полученный скалярно перемножают с третьим вектором. Смешанное произведение представляет собой число – число. Результат смешанного произведения – объем параллелепипеда, образованного векторами.

Свойства.

1. Смешанное произведение не меняется при циклической перестановке сомножителей:

2. Смешанное произведение не изменится при перемене местами векторного и скалярного произведения.

3. Смешанное произведение меняет знак при перемене мест любых двух векторовсомножителей.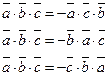

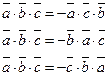
4. Смешанное произведение трех ненулевых векторов равно нулю тогда и только тогда, когда они компланарны.

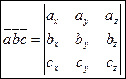
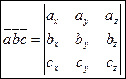
Три вектора называются компланарными, если результат смешанного произведения равен нулю.

16. Линейные преобразования пространства. Матрица линейного преобразования. Связь между координатами образа и прообраза.

Рассмотрим линейное пространство V, в котором каждому элементу x, в силу некоторого закона поставлен элемент этого же пространства.

прообраз

образ

Каждому прообразу соответствует единственный образ.

Каждый образ имеет единственный прообраз.

Линейное преобразование пространства, при котором существует взаимнооднозначные соответствия.

Блективное преобразование – называется линейным, если выполняются 2 условия.

1.

2.

Рассмотрим nмерное линейное пространство

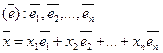
Для того, чтобы задать линейные преобразования в этом пространстве достаточно задать это преобразование для базисных векторов.

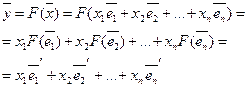
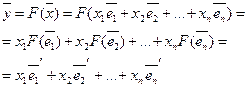
Матрица линейного преобразования.

Пусть F – линейное преобразование линейного пространства, переводящая базис в базис . Т.к. базис, то верны соотношения

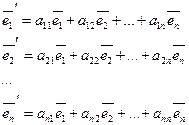
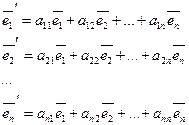
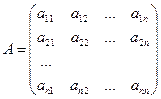
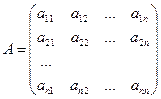
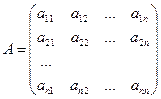
А – является матрицей линейного преобразования или линейным оператором пространства.

Связь между координатами образа и прообраза.

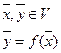
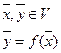
В базисе вектор имеет координаты

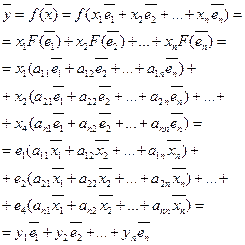
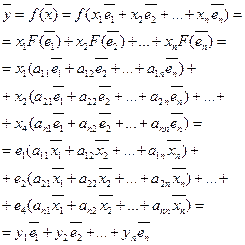
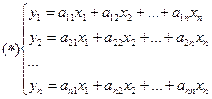
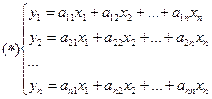
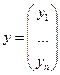
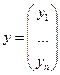
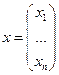
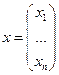
Линейное преобразование – матрица линейного оператора.

Каждому линейному преобразованию соответствует 1 матрица линейного оператора и наоборот.

Если имеется квадратная матрица задано линейное преобразование пространства.

17. Связь между координатами одного и того же линейного оператора в разных базисах.

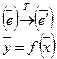
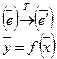
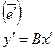
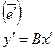
Т – матрица перехода от e к e’ , то:

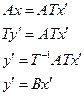
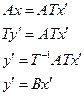
Если линейный оператор имеет в базисе невырожденную матрицу Т, матрица этого оператора в любом другом базисе не будет вырождена.

18. Характеристическое уравнение линейного оператора. Собственные векторы линейного оператора и их свойства.

Если в базисе линейный оператор имеет матрицу А, а в базисе () оператор имеет матрицу В

λ – произвольное число ≠0

Е – единичная матрица

Если характеристически многочлен линейного оператора прировнять к 0, получим характеристическое уравнение линейного оператора.

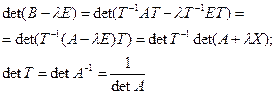
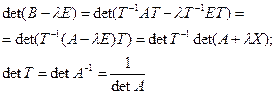
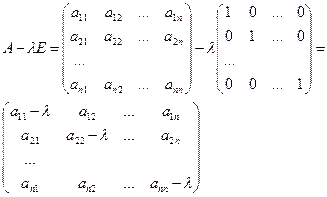
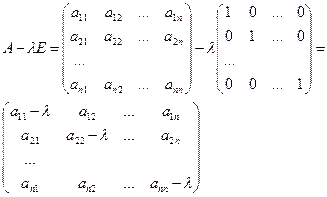
Собственные векторы линейного оператора

Ненулевой вектор называется собственным вектором линейного оператора, если оператор к , получим этот же , умноженный на некоторое к.

к – собственное число оператора А=

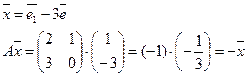
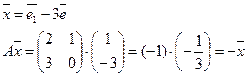
Каждый собственный вектор имеет единственное собственное число.

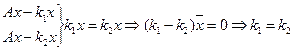
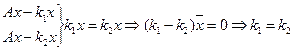
19. Прямая в пространстве. Виды уравнений прямой. Угол между прямыми.

Векторное уравнение прямой.

Положение прямой можно задать по точке и направляющему вектору.

Пусть прямая Lзадана ее точкой M₀ (x₀ ;y₀ ;z₀ ) и направляющим вектором S(m;n;p). Возьмем на прямой Lточку M(x;y;z). Обозначим радиусвекторы точек Mи M₀ через rи r₀ .

Тогда уравнение прямой запишется в виде:

где t – скалярный множитель (параметр).

Параметрические уравнения прямой.

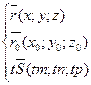
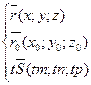
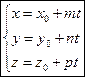
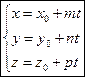
Канонические уравнения прямой.

S(m;n;p) – направляющий вектор прямой L. M₀ (x₀ ;y₀ ;z₀ ) – точка на прямой. соединяет M₀ с произвольной точкой М.

Уравнение прямой в пространстве, проходящей через две точки.

M₁ (x₁ ;y₁ ;z₁ ) M₂ (x₂ ;y₂ ;z₂ )

В качестве направляющего вектора можно задать вектор

Следовательно:

, тогда

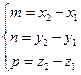
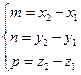
Общее уравнение прямой.

Уравнение прямой как линию пересечения двух плоскостей. Рассмотрим:

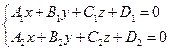
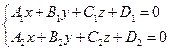
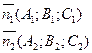
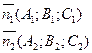
Т.к. прямая перпендикулярна векторам n₁ и n₂ то направляющий вектор запишется как векторное произведение:

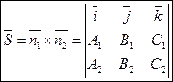
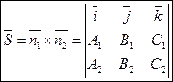
Угол между прямыми.

;

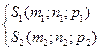
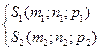
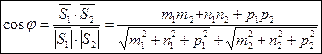
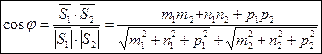
20. Плоскость в пространстве. Виды уравнения плоскостей. Угол между плоскостями.

Уравнение плоскости, проходящей через заданную точку, перпендикулярно данному вектору.

Пусть плоскость задана точкой M₀ (x₀ ;y₀ ;z₀ ) и вектором , перпендикулярной этой плоскости.

Возьмем произвольную точку M(x;y;z) и составим вектор . При любом расположении точки М на плоскости Q, поэтому .

Общее уравнение плоскости.

·Если D=0, то данному уравнению удовлетворяет точка О (0;0;0)

·Если С=0 то вектор . Следовательно, плоскость параллельна оси oz, если В=0 – то oy, если А=0 – то ox.

·Если C=D=0, то плоскость проходит через О (0;0;0), параллельно оси oz. Аналогично при A=D=0 и B=D=0.

·Если А=В=0 то уравнение примет вид плоскость параллельна плоскости Oxy.

·Если A=B=D=0, то уравнение имеет вид . Это уравнение плоскости Oxy.

Уравнение плоскости, проходящей через три точки

К (х₁ ;у₁ ) М (х₂ ;у₂ ) N (x₃ ;y₃ )

Возьмем на плоскости точку P (x;y;z).

Составим векторы:

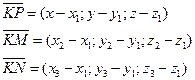
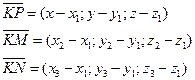
Эти векторы лежат в одной плоскости, следовательно они компланарны:

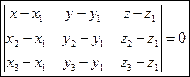
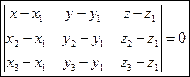
Уравнение плоскости в отрезках.

Пусть плоскость отсекает на осях отрезки, т.е. проходит через точки:

; ;

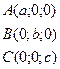
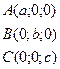
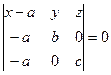
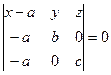
Нормальное уравнение плоскости.

21. Угол между прямой и плоскостью. Расстояние от точки до плоскости.

Прямая L:

Пусть φ – угол между плоскостью и прямой.

Тогда θ – угол между и.

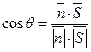
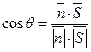
Найдем , если

, т.к.

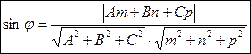
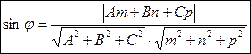
Расстояние от точки до плоскости.

Дано:

M₀ (x₀ ;y₀ ;z₀ )

Расстояние dот точки М₀ до плоскости ∆ равно модулю проекции вектора (где М₁ (x₁ ;y₁ ;z­₁ ) произвольная точка плоскости) на направление нормального вектора

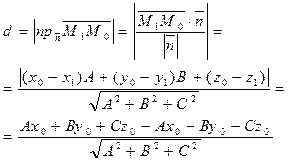
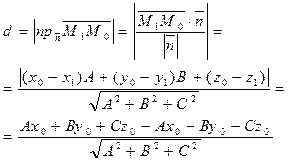
!!!Если плоскость задана уравнением:

то расстояние до плоскости находится по формуле:

22. Прямая на плоскости. Виды уравнений прямой на плоскости. Угол между двумя прямыми.

Уравнение с угловым коэффициентом.

k= tgα – угловой коэффициент.

Если b=0 то прямая проходит через начало координат. Уравнение примет вид

Если α=0, то k = tgα = 0. То прямая пройдет параллельно оси ох.

Если α=π/2, то уравнение теряет смысл. В этом случае уравнение примет вид и пройдет параллельно оси оу.

Общее уравнение прямой.

A, B, C – произвольные числа, причем А и В не равны нулю одновременно.

·Если В=0, то уравнение имеет вид или . Это уравнение прямой, параллельной оси оу. и проходящей через точку

·Если В≠0, то получаем уравнение с угловым коэффициентом .

·Если А=0, то уравнение имеет вид . Это уравнение прямой, параллельной оси ох.

·Если С=0, то уравнение проходит через т. О (0;0).

Уравнение прямой, проходящей через точку, в данном направлении.

т М (х₀ ;у₀ ).

Уравнение прямой записывается в виде .

Подставим в это уравнение точку М

Решим систему:

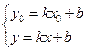
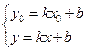
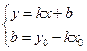
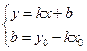
Уравнение прямой, проходящей через 2 точки.

К (х₁ ;у₁ ) М (х₂ ;у₂ )

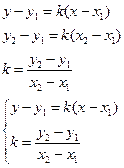
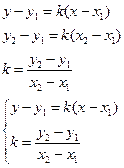
Уравнение прямой в отрезках.

К (а;0); М (0;b)

Подставим точки в уравнение прямой:

Уравнение прямой, проходящей через данную точку, перпендикулярно данному вектору.

М₀ (х₀ ;у₀ ).

Возьмем произвольную точку М (х;у).

Т.к. , то

Нормальное уравнение прямой.

Уравнение прямой можно записать в виде:

Т.к. ;, то:

Угол между прямыми.

Дано: прямые L₁ и L₂ с угловыми коэффициентами

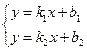
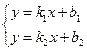
Требуется найти угол между прямыми:

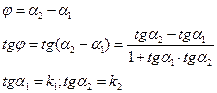
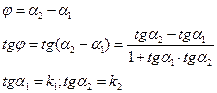
23. Эллипс. Определение. Вывод канонического уравнения.

Эллипсом называется

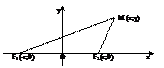
геометрическое место всех

точек плоскости, сумма

расстояний от которых до

до фокусов есть величина

постоянная, большая, чем расстояние между фокусами.

Пусть М (х;у) – произвольная точка эллипса.

Т.к. MF₁ + MF₂ = 2a

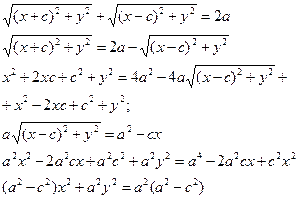
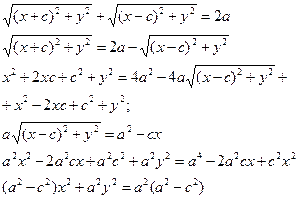
Т.к.

То получаем

Или

24. Гипербола. Определение. Вывод канонического уравнения.

Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до фокусов есть величина постоянная.

Пусть M(x;y) – произвольная точка гиперболы. Тогда согласно определению гиперболы |MF₁ – MF₂ |=2a или MF₁ – MF₂ =±2a,

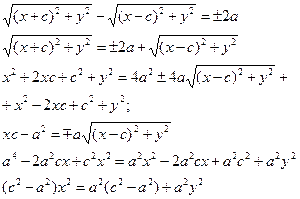
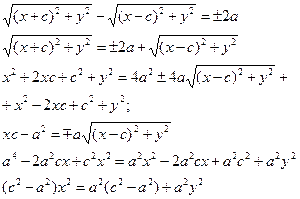
25. Парабола. Определение. Вывод канонического уравнения.

Парабола – множество всех точек плоскости, каждая из которых одинаково удалена от фокуса, и директрисы. Расстояние между фокусом и директрисой называется параметром параболы и обозначается через р>0.

Пусть M(x;y) – произвольная

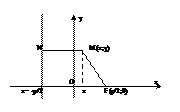
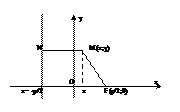
точка Mс F. Проведем отрезок

MN перпендикулярно

директрисе. Согласно

определению MF=MN.

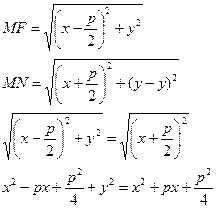
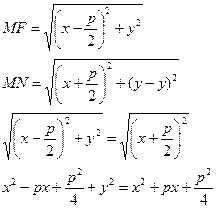
26. Поверхности вращения.

Поверхность, образованная вращением некоторой плоской кривой вокруг оси, лежащей в ее плоскости, называется поверхностью вращения. Пусть некоторая кривая L лежит в плоскости Oyz. Уравнение этой кривой запишутся в виде:

Найдем уравнение поверхности, образованной вращением кривой L вокруг оси Oz.

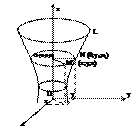
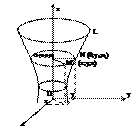
Возьмем на поверхности точку

M (x;y;z). Проведем через точку

М плоскость, перпендикулярную

оси oz, и обозначим точки

пересечения ее с осью oz

и кривой Lсоответственно O₁ и N.

Обозначим координаты точки

N (0;y₁ ;z₁ ). Отрезки O₁ Mи O₁ N

являются радиусами одной и той же окружности. Поэтому O₁ M= O₁ N. Но O₁ M = (x² +y² )^0.5 , O₁ N=|y₁ |.

Следовательно, |y₁ |=(x² +y² )^0.5 или y₁ =±(x² +y² )^0.5 . Кроме того, очевидно, z₁ =z.

Следовательно – искомое уравнение поверхности вращения, ему удовлетворяют координаты любой точка М этой поверхности и не удовлетворяет координаты точек, не лежащих на поверхности вращения.

27. Поверхности 2го порядка. Эллипсоид, Гиперболоид.

Эллипсоид.

Рассмотрим сечение поверхности с плоскостями, параллельными xOy. Уравнения таких плоскостей z=h, где h – любое число. Линия, получаемая в сечении, определяется двумя уравнениями:

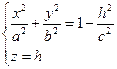
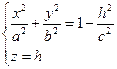
Если |h|>c, c>0, то точек пересечения поверхности с плоскостями z=h нет.

Если |h|=c, т.е. h=±c, то

Учебная работа № 1528. Шпоры по вышке