Учебная работа № 1375. Образцы исследования элементарных функций, содержащих обратные тригонометрические функции

Учебная работа № 1375. Образцы исследования элементарных функций, содержащих обратные тригонометрические функции

Примеры

Примеры: в нижеследующих примерах приведены образцы исследования элементарных функций, заданных формулами, содержащими обратные тригонометрические функции.

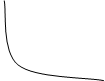
Пример №1. Исследовать функции arcsin(1/x) и arccos(1/y) и построить их графики.

Решение: Рассмотрим 1ю функцию

y

y

y = arcsin(1/x)

π/2

π/2

Д(f): | 1/x | ≤ 1 ,

| x | ≥ 1 ,

( ∞ ; 1 ] U [ 1; + ∞ )

y

x

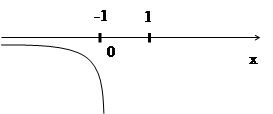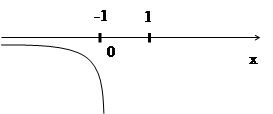Функция нечетная

( f(x) убывает на пр. [0;1] , f(y) убывает на пр. [0;π/2] )

y

Заметим, что функция y=arccosec(x) определяется из условий cosec(y)=x и y є [π/2; π/2], но из условия cosec(y)=x следует sin(y)=1/x, откуда

π

y=arcsin(1/x). Итак, arccos(1/x)=arcsec(x)

Д(f): ( ∞ ; 1 ] U [ 1; + ∞ )

Пример №2. Исследовать функцию y=arccos(x² ).

π/2

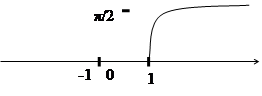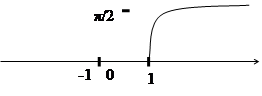Решение:

Д(f): [1;1]

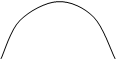
Четная

f(x) убывает на пр. [0;1]

1

0

f(x) возрастает на пр. [1;0]

1

x

Пример №3. Исследовать функцию y=arccos² (x).

Решение: Пусть z = arccos(x), тогда y = z²

f(z) убывает на пр. [1;1] от π до 0.

f(y) убывает на пр. [1;1] от π² до 0.

Пример №4. Исследовать функцию y=arctg(1/(x² 1))

Решение:

Д(f): ( ∞ ; 1 ) U ( 1; 1 ) U ( 1; +∞ )

Т.к. функция четная, то достаточно исследовать функцию на двух промежутках:

y

[ 0 ; 1 ) и ( 1 ; +∞ )

π/2 X	0	< x <	1	< x <	+∞
1 1 u=1/(x2 1)	1	↘	+ ∞ ∞	↘	0
0 x y=arctg(u)	π/4	↘	π/2 π/2	↘	0

π/4

π/2

Тригонометрические операции над аркфункциями

Тригонометрические функции от одного и того же аргумента выражаются алгебраически одна через другую, поэтому в результате выполнения какойлибо тригонометрической операции над любой из аркфункций получается алгебраическое выражение.

В силу определения аркфункций:

sin(arcsin(x)) = x , cos(arccos(x)) = x

(справедливо только для x є [1;1] )

tg(arctg(x)) = x , ctg(arcctg(x)) = x

(справедливо при любых x )

Графическое различие между функциями, заданными формулами:

y=x и y=sin(arcsin(x))

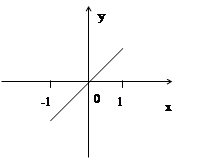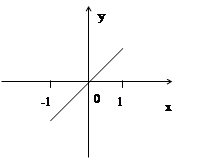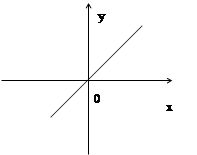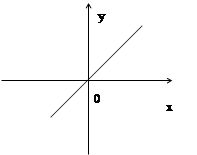Сводка формул, получающихся в результате выполнения простейших тригонометрических операций над аркфункциями.

Аргумент функция	arcsin(x)	arccos(x)	arctg(x)	arcctg(x)
sin	sin(arcsin(x))=x
cos		x
tg			x	1 / x
ctg			1 / x	x

Справедливость всех этих формул может быть установлена при помощи рассуждений, приведенных ниже:

1. Т.к. cos² x + sin² x = 1 и φ = arcsin(x)

Перед радикалом следует взять знак “+”, т.к. дуга принадлежит правой полуокружности (замкнутой) , на которой косинус неотрицательный.

Значит, имеем

2. Из тождества следует:

3. Имеем

4.

Ниже приведены образцы выполнения различных преобразований посредством выведения формул.

Пример №1. Преобразовать выражение

Решение: Применяем формулу , имеем:

Пример №2. Подобным же образом устанавливается справедливость тождеств:

Пример №3. Пользуясь

Пример №4. Аналогично можно доказать следующие тождества:

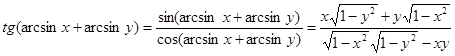
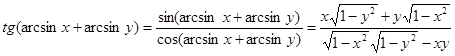
Пример №5. Положив в формулах

, и

, получим:

,

Пример №6. Преобразуем

Положив в формуле ,

Получим:

Перед радикалами взят знак “+”, т.к. дуга принадлежит I четверти, а потому левая часть неотрицательная.

Соотношения между аркфункциями

Соотношения первого рода – соотношения между аркфункциями, вытекающими из зависимости между тригонометрическими функциями дополнительных дуг.

Теорема. При всех допустимых х имеют место тождества:

arccos(x)

arcsin(x)

1

1

y

x

Соотношения второго рода – соотношения между аркфункциями, вытекающие из соотношений между значениями тригонометрических функций от одного и того же аргумента. Посредством соотношений 2го рода производятся преобразования одной аркфункции в другую (но от различных аргументов).

Случай №1. Значения двух данных аркфункций заключены в одной и той же полуокружности.

Пусть, например, рассматривается дуга α, заключенная в интервале (π/2; π/2).

Данная дуга может быть представлена как в виде арксинуса, так и в виде арктангенса. В самом деле, дуга имеет синус, равный sinα и заключена, так же как и α, в интервале (π/2; π/2), следовательно

Аналогично можно дугу α представить в виде арктангенса:

А если бы дуга α была заключена в интервале ( 0 ; π ), то она могла бы быть представлена как в виде арккосинуса, так и в виде арккотангенса:

Так, например:

Аналогично:

Формулы преобразования одних аркфункций в другие, значения которых содержаться в одной и той же полуокружности (правой или верхней).

1. Выражение через арктангенс.

Пусть , тогда

Дуга , по определению арктангенса, имеет тангенс, равный и расположена в интервале (π/2; π/2).

Дуга имеет тот же тангенс и расположена в том же интервале (π/2; π/2).

Следовательно,

(1)

(в интервале ( 1 : 1 )

2. Выражение через арксинус.

Т.к. , то (2)

в интервале

3. Выражение арккосинуса через арккотангенс. Из равенства следует тождество

(3)

Случай №2. Рассмотрим две аркфункции, значения которых выбираются в различных промежутках (например, арксинус и арккосинус; арккосинус и арктангенс и т.п.). Если аргумент какойлибо аркфункции (т.е. значение тригонометрической функции) положителен, то соответственно аркфункция (дуга), заключенная в первой четверти, может быть представлена при помощи любой аркфункции; так, например,

Поэтому каждая из аркфункций от положительного аргумента может быть выражена посредством любой другой аркфункции.

Значение какойлибо аркфункции от отрицательного аргумента принадлежит либо промежутку от π/2 до 0, либо промежутку от π/2 до π и не может быть представлено в виде аркфункции, значение которой принадлежит другому (из этих двух) промежутку.

Так, например, дуга не может быть значением арксинуса. В этом случае

Формулы преобразования одних аркфункций в другие, значения которых выбираются в различных полуокружностях.

4. Выражение арксинуса через арккосинус.

Пусть , если , то . Дуга имеет косинус, ра

Учебная работа № 1375. Образцы исследования элементарных функций, содержащих обратные тригонометрические функции