Учебная работа № 1140. Аксиоматика векторного пространства

Учебная работа № 1140. Аксиоматика векторного пространства

Глава 2

1. Некоторые векторные равенства

Среди векторных соотношений можно выделить несколько важных соотношений, называемых здесь основными. Эти основные соотношения являются, образно выражаясь, ключами к решению широкого класса задач.

I Основное соотношение. Во всяком треугольнике ЛВС выполняется равенство

(I)

Где М – центроид (точка пересечения медиан) треугольника АВС.

Докажем соотношение (I).

Пусть М – центроид треугольника АВС. Соединим точку М со всеми вершинами треугольника. Прямая МВ пересекает сторону АС треугольника АВС в точке О, являющейся серединой стороны АС. На прямой ВМ откладываем МЕ = ВМ и соединяем точку Е с вершинами А и С. очевидно, что АМСЕ –параллелограмм. Поэтому . Откуда . Так как , то . Ч.т.д.

Задача. Доказать, что если М – центроид треугольника АВС и О произвольная точка пространства, то выполняется равенство

(1)

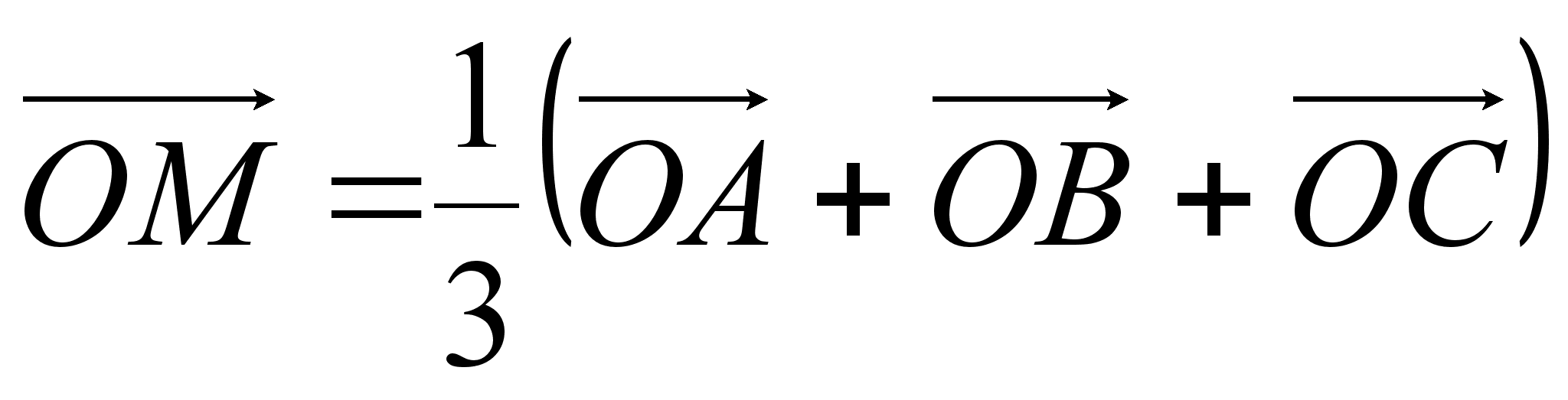
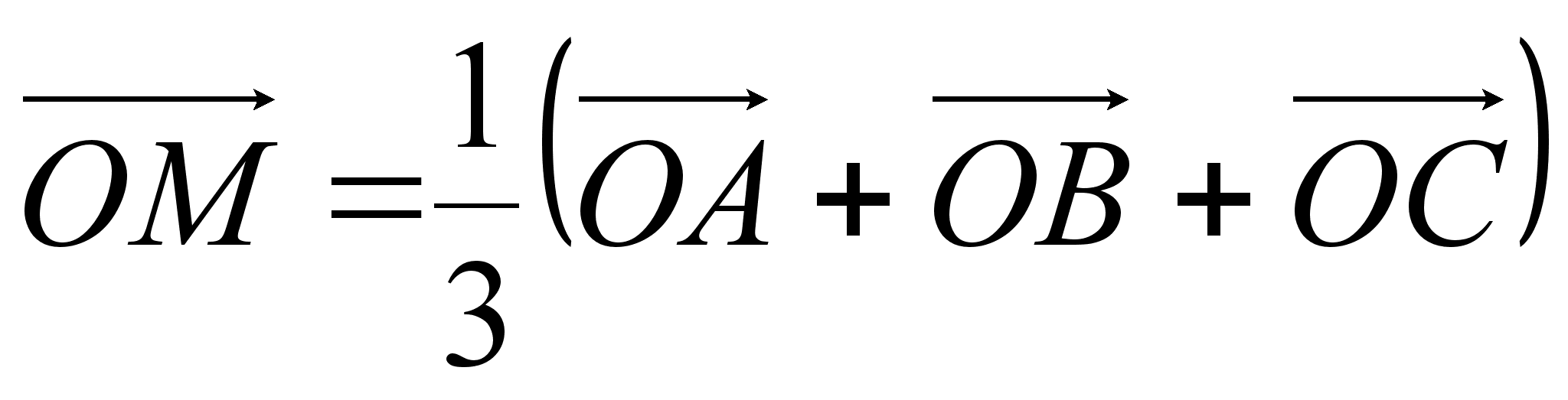
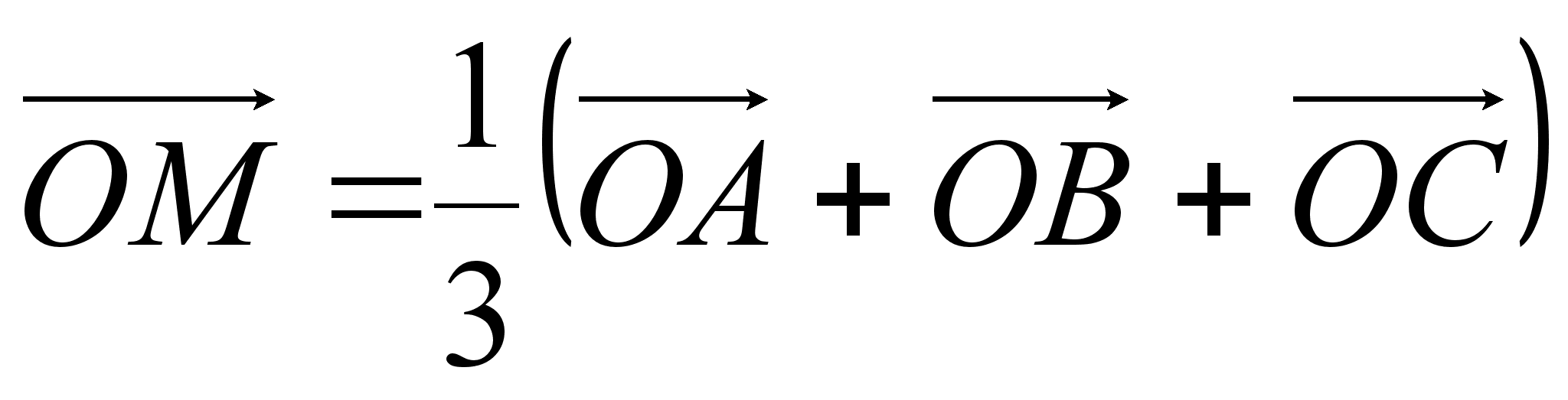
Доказательство:

Запишем следующие векторные равенства:

Сложив эти равенства по частям, получаем:

,

откуда

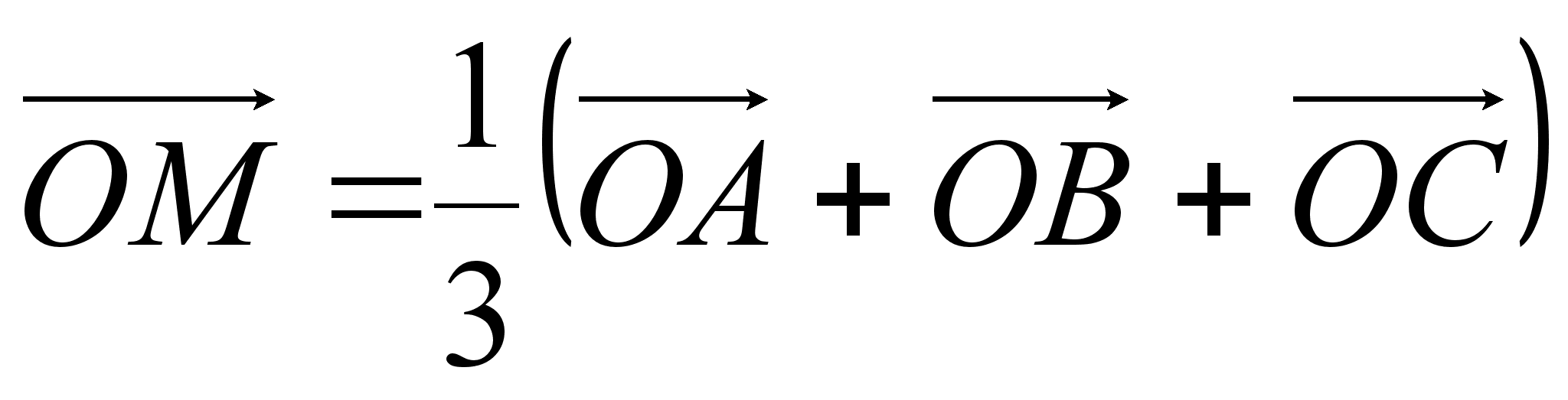
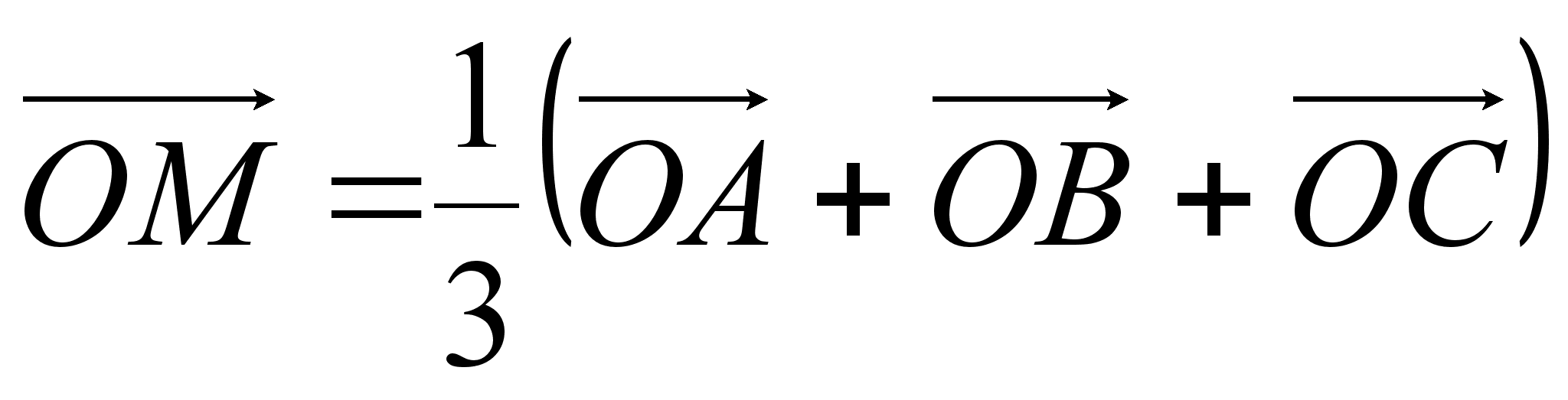
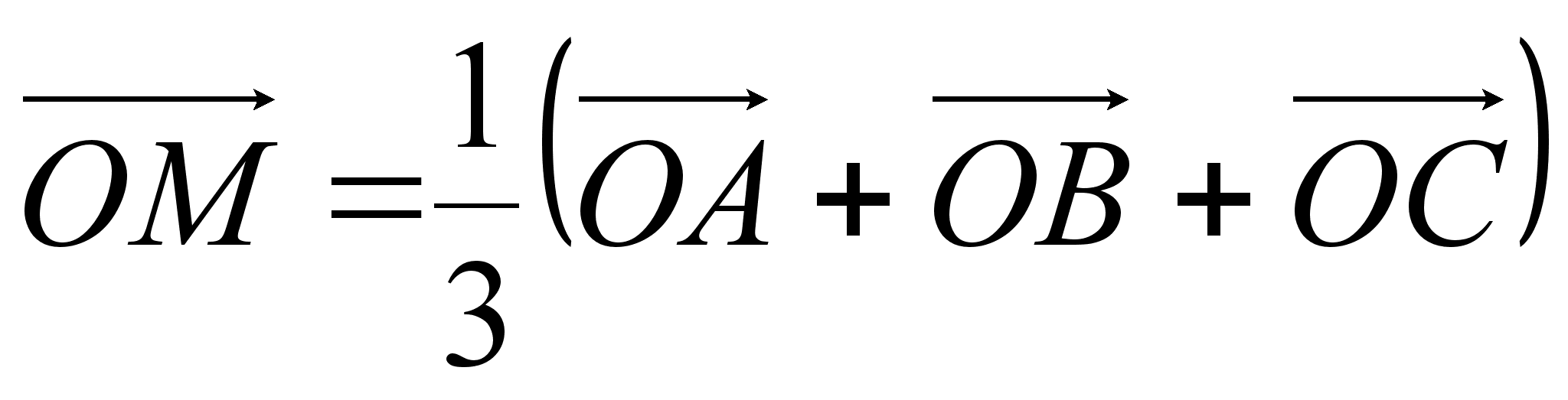
Доказанное равенство также следует отнести к основным векторным соотношениям, так как оно часто используется в решении многих задач.

II Основное соотношения. В треугольнике АВС на стороне АС взята точка D так, что АD : DС = m : n.

Тогда имеет месть следующее соотношение:

(II)

Доказательство:

Из треугольника АВС имеем:

.

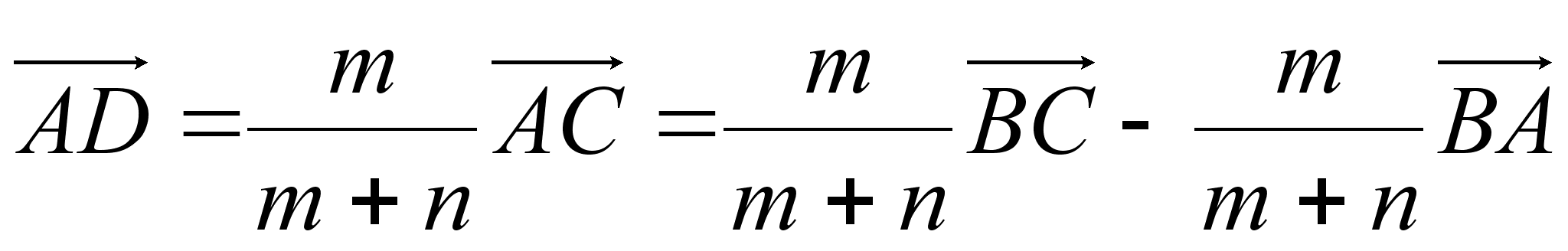
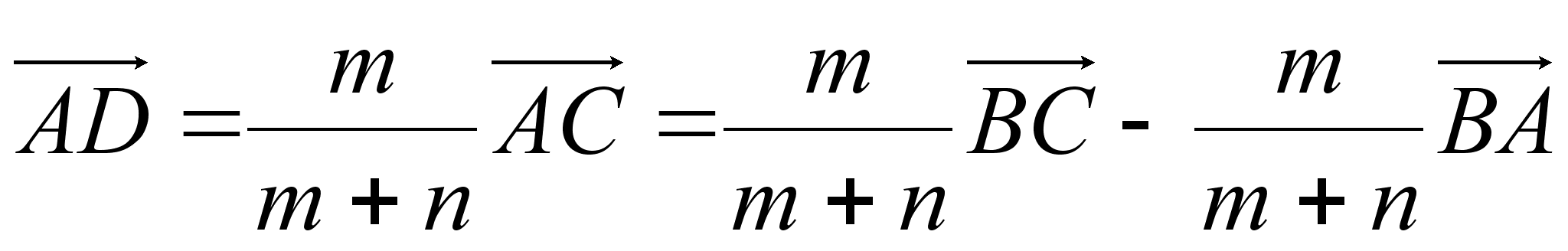
Ч.т.д.

Задача. Через середину Е медианы СС₁ треугольника АВС проведена прямая АЕ, пересекающая сторону ВС в точке F. Вычислить АЕ : ЕF и СF : FВ.

Решение.

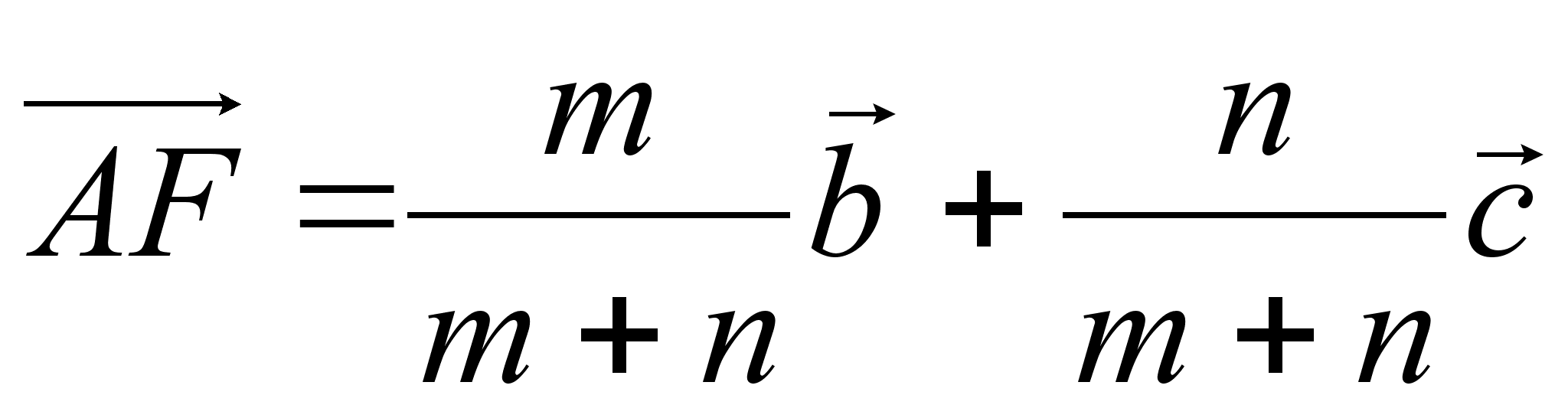
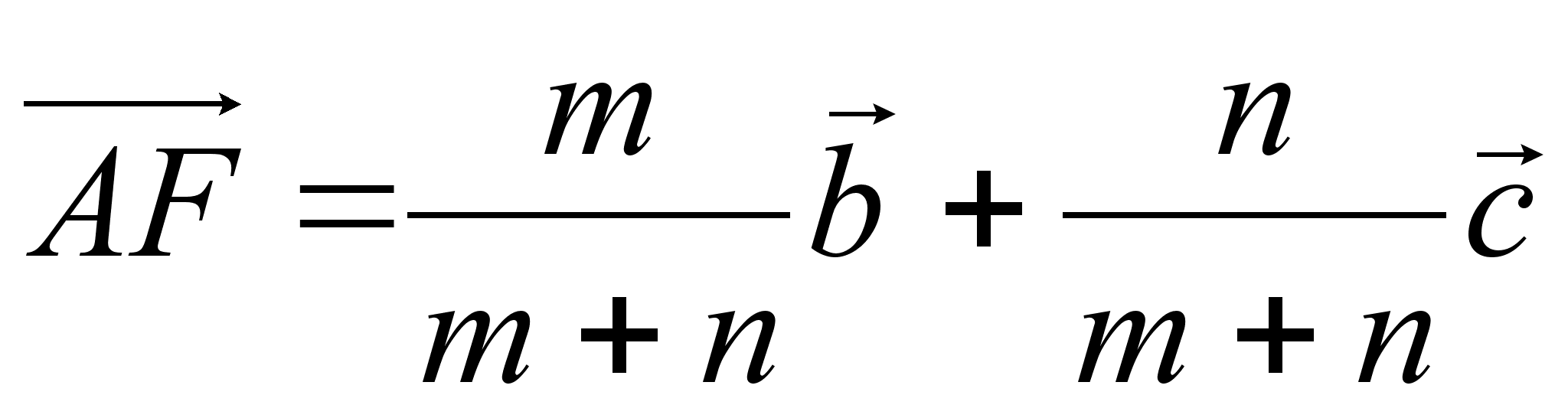
Введем векторы и . Пусть СF : FВ = m : n. Тогда по формуле (II) имеем:

и (1)

где 0 < х < 1.

С другой стороны, учитывая, что Е – середина медианы СС₁ получаем для АЕ следующее выражение:

(2)

В силу единственности разложения вектора по двум векторам из (1) и (2) получаем систему:

(3)

Разделив по частям первое уравнение системы (3) на второе, получаем, что m : n = 1 : 2, т.е. СF : FВ = 1 : 2.

Сложив по частям уравнение системы (3), находим, что , т.е. AE : EF = 3 : 4

III Основное соотношение. Если точки М и N делят отрезки АВ и CD соответственно в равных отношениях так, что AM : MB = CN : ND = m : n, то выполняется равенство.

(III)

Доказательство:

Для доказательства равенства (III)
мы воспользуемся формулой (II). Запишем, что отрезки АВ и CD могут произвольно располагаться относительно друг друга (например, они могут лежать на скрещивающихся прямых и на прямых, принадлежащих одной плоскости).

Пусть О произвольная точка, не принадлежащая ни отрезку АВ, ни отрезку CD. Соединим точку О с точками А, М, В, С, N и D и раcсмотрим векторы и .

Имеем:

,

,

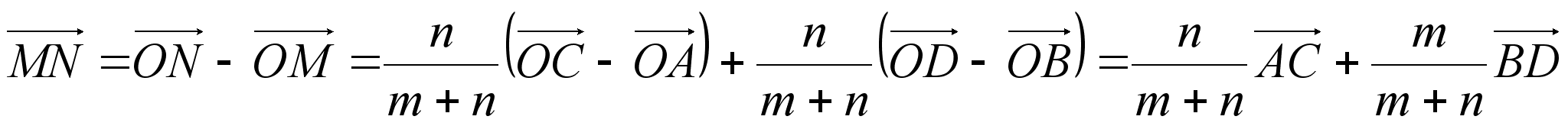
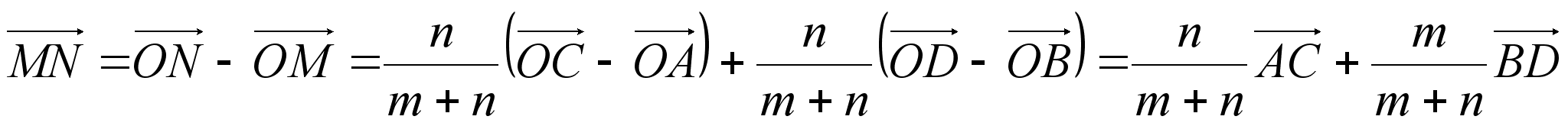
Ч. т. д.

Задача. На прямой m даны три точки Р, Q, R, а на прямой m₁ три точки P₁, Q₁, R₁ причем , . Доказать, что середины отрезков PP₁, QQ₁ и RR₁ принадлежат одной прямой.

Решение.

Пусть М, N и К середины отрезков РР₁ QQ₁ и RR₁ соответственно.

На основании (III) запишем следующие векторные равенства:

(1)

(2)

Из (1) и (2) следует, что векторы и коллинеарные. А так как начало одного из них является концом другого, то точки М, N и К принадлежат одной прямой.

IV Основное соотношение. Дан тетраэдр ABCD и в плоскости его грани ABC точка М. Доказать, что для разложения

Выполняется равенство

Доказательство:

Допустим, что точка М лежит внутри треугольника ABC. Проведем через точки А и М прямую, которая пересекает сторону ВС в точке Е. Пусть Е делит сторону

Учебная работа № 1140. Аксиоматика векторного пространства