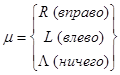Учебная работа № 1120. Математическая Логика

Учебная работа № 1120. Математическая Логика

Конспекты лекций по математической логике.

1. Теория алгоритмов

1.1 Различные подходы к определению алгоритма:

1⁰ . Неформальное понятие алгоритма (последовательность инструкций для выполнения действия).

2⁰ . Машина с неограниченными регистрами (МНР).

3⁰ Машина Тьюринга – Поста (МТП).

4⁰ Нормальные алгоритмы Маркова (НАМ).

1.1.1 Машина с неограниченными регистрами (МНР).

Имеется некое устройство, в котором счетное число ячеек памяти (регистров), в которых хранятся целые числа.

Допустимые команды:

Z(n) обнуление регистра R_n .

S(n) увеличение числа в регистре R_n на 1.

T(m,n) копирует содержимое R_m в регистор R_n .

I(p,q,n) если содержимое R_p = R_q то выполняется команда с номером n , если нет

следующая.

Программа для МНР должна быть последовательностью команд Z, S, T, I с определенным порядком, выполняемые последовательно.

Тезис Черча ( Churcha ) : Первое и второе определение алгоритма эквивалентны между собой. Любой неформальный алгоритм может быть представлен в программе для МНР.

1.1.2 Машина Тьюринга Поста.

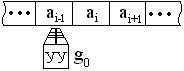
Имеется устройство просматривающее бесконечную ленту, где есть ячейки содержащие элементы алфавита: , где пустой символ (пустое слово), который может принадлежать и не принадлежать А . Также существует управляющая головка (устройство) (УУ)/(УГ), которая в начальный момент расположена в определенном месте, в состоянии. Также существуют внутренние состояния машины:

Слово в данном алфавите любая конечная упорядоченная последовательность букв данного алфавита, притом длина слова это количество букв в нем (у пустого слова длина 0).

Допустимые команды:

1) ,где . 2) (остановка программы).

Последовательность команд называется программой , если в этой последовательности не встречается команд с одинаковыми левыми частями. Машина останавливается если она не находит команды с левой частью подобной текущей.

1.1.3 Нормальные алгоритмы Маркова.

Тип машины перерабатывающий слова, в которой существует некий алфавит , для которого W множество всех слов.

Допустимые команды: (Для машин этого типа важна последовательность команд.)

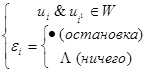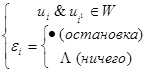где	Пример: Программа:

1.1.4 Реализация функции натурального переменного.

но мы допускаем не всюду определенную функцию.

то это означает, что

притом ,если f не определена, то и программа не должна ничего выдавать.

притом ,если f не определена, то и программа не должна ничего выдавать.

(, а числа представляются в виде ,например .)

1.2 Эквивалентность трех подходов к понятию алгоритм.

1.2.1 Теорема об эквивалентности понятия вычислимой функции.

вычислима: ()

1) Если существует программа МНР, которая вычисляет эту функцию.

2) Если существует программа МТП, которая вычисляет эту функцию.

3) Если существует программа НАМ, которая вычисляет эту функцию.

Использование НАМ:

Теор .: Классы функций вычислимых на МТП, с помощью НАМ и с помощью МНР совпадают.

Пусть которая вычисляется на МТП, вычислим её на НАМ.

МТП:

НАМ:

Команда МТП: преобразуется по правилам:

Команда МТП:

2. Булевы функции.

2.1 Основные определения

2.1.1 Декартово произведение

мнво всевозможных упорядоченных пар элементов из А и В.

Пример :

2.1.2 Декартова степень произвольного множества.

Опр : множество всевозможных упорядоченных наборов длины n , элементов множества А.

2.1.3 Определение булевой функции от n переменных.

Любое отображение называется булевой функцией от n переменных, притом множество

2.1.4 Примеры булевой функции.

1) логическая сумма (дизъюнкция).

2) логическое умножение (конъюнкция).

3) сложение по модулю два.

4) логическое следствие (импликация).

5) отрицание.

2.1.5 Основные булевы тождества.

1) (ассоциативность)

2) (коммутативность)

3) (свойство нуля)

4) (закон поглощения для 1)

5) (ассоциативность)

6) (коммутативность)

7)

Учебная работа № 1120. Математическая Логика